基于matlab实现蚁狮优化算法_蚁狮优化算法资源-CSDN文库

共8个文件

m：7个

pdf：1个

版权申诉

7 浏览量 2024-04-14 22:12:34 上传评论收藏 2.37MB ZIP 举报

蚁狮优化算法（Ant Lion Optimizer，ALO）是一种生物启发式优化算法，源自自然界中蚁狮建造陷阱捕食蚂蚁的现象。在MATLAB环境中实现这种算法，可以解决各种工程问题和数学优化问题。MATLAB是一种强大的数值计算软件，广泛应用于科学研究、工程计算以及数据分析等领域。蚁狮优化算法的核心原理是模拟蚁狮在寻找食物源（最优解）的过程中，通过分泌信息素引导蚂蚁（搜索代理）探索环境。蚁狮会在地表挖坑形成陷阱，蚂蚁会依据信息素浓度和距离信息选择路径，而蚁狮则根据蚂蚁的路径更新信息素。随着迭代过程的进行，蚁群逐渐聚集在最优解附近，最终找到全局最优解。在MATLAB中实现ALO，首先需要定义问题的目标函数，即要优化的函数。接着，设置算法的参数，如种群大小、迭代次数、信息素蒸发率、信息素更新权重等。然后，初始化蚁狮的位置，随机生成在可行域内的解。接下来，进入主循环，执行以下步骤： 1. **蚂蚁运动**：每个蚂蚁根据当前信息素浓度和距离信息，计算出前往下一个位置的概率，并进行移动。 2. **信息素更新**：根据蚂蚁路径的质量，蚁狮在路径上更新信息素。优秀路径上的信息素会增加，而较差路径的信息素会减少。 3. **信息素蒸发**：为了防止信息素过快积累，需要设定一定的信息素蒸发率，使得旧的信息素逐渐减少。 4. **记录最优解**：在每一代结束后，记录下当前最优解。 5. **判断终止条件**：若达到预设的迭代次数或者最优解的变化小于预设阈值，算法结束。在实现过程中，需要注意以下几点： - **并行计算**：MATLAB支持并行计算工具箱，可以通过并行化处理来加速算法的运行。 - **适应度函数**：目标函数可能需要转换为适应度函数，以适应ALO的优化过程。 - **参数调优**：算法性能受参数影响很大，需要通过实验调整合适的参数值。 - **可视化**：通过绘制迭代过程中的目标函数值变化图和最优解轨迹图，可以帮助理解算法的收敛行为。此外，还需要编写适当的输入输出接口，以便用户能够方便地输入待优化问题和获取结果。将所有代码封装成一个函数或类，便于重复使用和维护。通过以上步骤，我们可以在MATLAB中实现一个完整的蚁狮优化算法，用于解决各种优化问题，包括但不限于连续函数优化、组合优化、参数估计等。这不仅能够提高问题求解的效率，还能利用MATLAB丰富的工具箱和图形界面，为用户带来便捷的体验。

资源推荐

资源详情

资源评论

收起资源包目录

基于matlab实现蚁狮优化算法.zip （8个子文件）

基于matlab实现蚁狮优化算法

3038ALO（蚁狮优化算法）

RouletteWheelSelection.m 2KB

initialization.m 2KB

main.m 3KB

ALO.m 6KB

Random_walk_around_antlion.m 3KB

Get_Functions_details.m 8KB

func_plot.m 4KB

Fardapaper-The-Ant-Lion-Optimizer.pdf 2.96MB

The Ant Lion Optimizer

Seyedali Mirjalili

⇑

School of Information and Communication Technology, Grifﬁth University, Nathan, Brisbane, QLD 4111, Australia

Queensland Institute of Business and Technology, Mt Gravatt, Brisbane, QLD 4122, Australia

article info

Article history:

Received 14 December 2014

Received in revised form 9 January 2015

Accepted 13 January 2015

Available online 3 March 2015

Keywords:

Optimization

Benchmark

Constrained optimization

Particle swarm optimization

Algorithm

Heuristic algorithm

Genetic algorithm

abstract

This paper proposes a novel nature-inspired algorithm called Ant Lion Optimizer (ALO). The ALO

algorithm mimics the hunting mechanism of antlions in nature. Five main steps of hunting prey such

as the random walk of ants, building traps, entrapment of ants in traps, catching preys, and re-building

traps are implemented. The proposed algorithm is benchmarked in three phases. Firstly, a set of 19

mathematical functions is employed to test different characteristics of ALO. Secondly, three classical

engineering problems (three-bar truss design, cantilever beam design, and gear train design) are solved

by ALO. Finally, the shapes of two ship propellers are optimized by ALO as challenging constrained real

problems. In the ﬁrst two test phases, the ALO algorithm is compared with a variety of algorithms in the

literature. The results of the test functions prove that the proposed algorithm is able to provide very com-

petitive results in terms of improved exploration, local optima avoidance, exploitation, and convergence.

The ALO algorithm also ﬁnds superior optimal designs for the majority of classical engineering problems

employed, showing that this algorithm has merits in solving constrained problems with diverse search

spaces. The optimal shapes obtained for the ship propellers demonstrate the applicability of the proposed

algorithm in solving real problems with unknown search spaces as well. Note that the source codes of the

proposed ALO algorithm are publicly available at http://www.alimirjalili.com/ALO.html.

1. Introduction

In recent years metaheuristic algorithms have been used as pri-

mary techniques for obtaining the optimal solutions of real engi-

neering design optimization problems [1–3]. Such algorithms

mostly beneﬁt from stochastic operators [4] that make them dis-

tinct from deterministic approaches. A deterministic algorithm

[5–7] reliably determines the same answer for a given problem

with a similar initial starting point. However, this behaviour results

in local optima entrapment, which can be considered as a disad-

vantage for deterministic optimization techniques [8]. Local

optima stagnation refers to the entrapment of an algorithm in local

solutions and consequently failure in ﬁnding the true global opti-

mum. Since real problems have extremely large numbers of local

solutions, deterministic algorithms lose their reliability in ﬁnding

the global optimum.

Stochastic optimization (metaheuristic) algorithms [9] refer to

the family of algorithms with stochastic operators including evolu-

tionary algorithms [10]. Randomness is the main characteristic of

stochastic algorithms [11]. This means that they utilize random

operators when seeking for global optima in search spaces.

Although the randomised nature of such techniques might make

them unreliable in obtaining a similar solution in each run, they

are able to avoid local solutions much easier than deterministic

algorithms. The stochastic behaviour also results in obtaining dif-

ferent solutions for a given problem in each run [12].

Evolutionary algorithms search for the global optimum in a

search space by creating one or more random solutions for a given

problem [13]. This set is called the set of candidate solutions. The

set of candidates is then improved iteratively until the satisfaction

of a terminating condition. The improvement can be considered as

ﬁnding a more accurate approximation of the global optimum than

the initial random guesses. This mechanism brings evolutionary

algorithms several intrinsic advantages: problem independency,

derivation independency, local optima avoidance, and simplicity.

Problem and derivation independencies originate from the con-

sideration of problems as a black box. Evolutionary algorithms only

utilize the problem formulation for evaluating the set of candidate

solutions. The main process of optimization is done completely inde-

pendent from the problem and based on the provided inputs and

received outputs. Therefore, the nature of the problem is not a con-

cern, yet the representation is the key step when utilizing evolution-

ary algorithms. This is the same reason why evolutionary algorithms

do not need to derivate the problem for obtaining its global optimum.

http://dx.doi.org/10.1016/j.advengsoft.2015.01.010

⇑

Address: School of Information and Communication Technology, Grifﬁth

University, Nathan, Brisbane, QLD 4111, Australia.

E-mail address: seyedali.mirjalili@grifﬁthuni.edu.au

URL: http://www.alimirjalili.com

Advances in Engineering Software 83 (2015) 80–98

Contents lists available at ScienceDirect

Advances in Engineering Software

journal homepage: www.elsevier.com/locate/advengsoft

As another advantage, local optima avoidance is high due the

stochastic nature of evolutionary algorithms. If an evolutionary

algorithm is trapped in a local optimum, stochastic operator lead

to random changes in the solution and eventually escaping from

the local optimum. Although there is no guarantee for resolving this

issue completely, stochastic algorithms have much higher probabil-

ity to escape from local optima compared to deterministic methods.

A very accurate approximation of the global optimum is not guaran-

teed as well, but with running an evolutionary algorithm several

times the probability of obtaining a better solution is increased.

Last but not least, the simplicity is another characteristic of evo-

lutionary algorithms. Natural evolutionary concepts or collective

behaviours are the main inspirations for the majority of algorithms

in this ﬁeld where they are so simple. In addition, evolutionary

algorithms follow a general and common framework, in which a

set of randomly created solutions is enhanced or evolved itera-

tively. What makes algorithms different in this ﬁeld is the method

of improving this set.

Some of the most popular algorithms in this ﬁeld are: Genetic

Algorithms (GA) [14,15], Particle Swarm Optimization (PSO) [16],

Ant Colony Optimization (ACO) [17], Differential Evolution (DE)

[18], Evolutionary Programming (EP) [19] [20]. Although these

algorithms are able to solve many real and challenging problems,

the so-called No Free Lunch theorem [21] allows researchers to

propose new algorithms. According to this theorem, all algorithms

perform equal when solving all optimization problems. Therefore,

one algorithm can be very effective in solving one set of problems

but in effective on a different set of problems. This is the founda-

tion of many works in this ﬁeld. Some of the recent algorithms

are: Grey Wolf Optimizer (GWO) [22], Artiﬁcial Bee Colony (ABC)

algorithm [23], Fireﬂy Algorithm (FA) [24,25], Cuckoo Search (CS)

algorithm [26,27], Cuckoo Optimization Algorithm (COA) [28],

Gravitational Search Algorithm (GSA) [29], Charged System Search

(CSS) [30–33], Magnetic Charged System Search [34,35], Ray Opti-

mization (RO) [36–38] algorithm, Colliding Bodies Optimization

(CBO) [39–44] algorithm, Hybrid Particle Swallow Swarm Optimi-

zation (HPSSO) [45], Democratic Particle Swarm Optimization

(DPSO) [46,47], Dolphin Echolocation (DE) [48,49], and Chaotic

Swarming of Particles (CSP) [50].

This paper also proposes a new algorithm called Ant Lion Opti-

mizer (ALO) as an alternative approach for solving optimization

problems. As its name implies, the ALO algorithm mimics the intel-

ligent behaviour of antlions in hunting ants in nature. The rest of

the paper is organized as follows:

Section 2 presents the main inspiration of this paper and pro-

poses the ALO algorithm. Experimental results of the test functions

are provided in Section 3. Sections 4 and 5 solve several real prob-

lems to demonstrate the applicability of the proposed algorithm.

Finally, Section 6 concludes the work and discusses possible future

research.

2. Ant Lion Optimizer

In this section the inspiration of the ALO algorithm is ﬁrst pre-

sented. The mathematical model and the ALO algorithm are then

discussed in details.

2.1. Inspiration

Antlions (doodlebugs) belong to the Myrmeleontidae family

and Neuroptera order (net-winged insects). The lifecycle of ant-

lions includes two main phases: larvae and adult. A natural total

lifespan can take up to 3 years, which mostly occurs in larvae (only

3–5 weeks for adulthood). Antlions undergo metamorphosis in a

cocoon to become adult. They mostly hunt in larvae and the adult-

hood period is for reproduction.

Their names originate from their unique hunting behaviour and

their favourite prey. An antlion larvae digs a cone-shaped pit in

sand by moving along a circular path and throwing out sands with

its massive jaw [51,52]. Fig. 1(a) shows several cone-shaped pits

with different sizes. After digging the trap, the larvae hides under-

neath the bottom of the cone (as a sit-and-wait predator [53]) and

waits for insects (preferably ant) to be trapped in the pit [53] as

illustrated in Fig. 1(b). The edge of the cone is sharp enough for

insects to fall to the bottom of the trap easily. Once the antlion

realizes that a prey is in the trap, it tries to catch it. However,

insects usually are not caught immediately and try to escape from

the trap. In this case, antlions intelligently throw sands towards to

edge of the pit to slide the prey into the bottom of the pit. When a

prey is caught into the jaw, it is pulled under the soil and con-

sumed. After consuming the prey, antlions throw the leftovers out-

side the pit and amend the pit for the next hunt.

Another interesting behaviour that has been observed in life

style of antlions is the relevancy of the size of the trap and two

things: level of hunger and shape of the moon. Antlions tend to

dig out larger traps as they become more hungry [54] and/or when

the moon is full [55]. They have been evolved and adapted this way

to improve their chance of survival. It also has been discovered that

an antlion does not directly observe the shape of the moon to

decide about the size of the trap, but it has an internal lunar clock

to make such decisions [55].

The main inspiration of the ALO algorithm comes from the for-

aging behaviour of antlion’s larvae. In the next subsection the

behaviour of antlions and their prey in nature is ﬁrst modelled

mathematically. An optimization algorithm is then proposed based

on the mathematical model.

2.2. Operators of the ALO algorithm

The ALO algorithm mimics interaction between antlions and

ants in the trap. To model such interactions, ants are required to

move over the search space, and antlions are allowed to hunt them

and become ﬁtter using traps. Since ants move stochastically in

nature when searching for food, a random walk is chosen for mod-

elling ants’ movement as follows:

XðtÞ¼½0; cumsumð2rðt

Þ1Þ; cumsumð2rðt

Þ1Þ;...; cumsumð2rðt

Þ1Þ

ð2:1Þ

where cumsum calculates the cumulative sum, n is the maximum

number of iteration, t shows the step of random walk (iteration in

this study), and r(t) is a stochastic function deﬁned as follows:

rðtÞ¼

1 if rand > 0:5

0 if rand 6 0:5



ð2:2Þ

where t shows the step of random walk (iteration in this study) and

rand is a random number generated with uniform distribution in

the interval of [0,1].

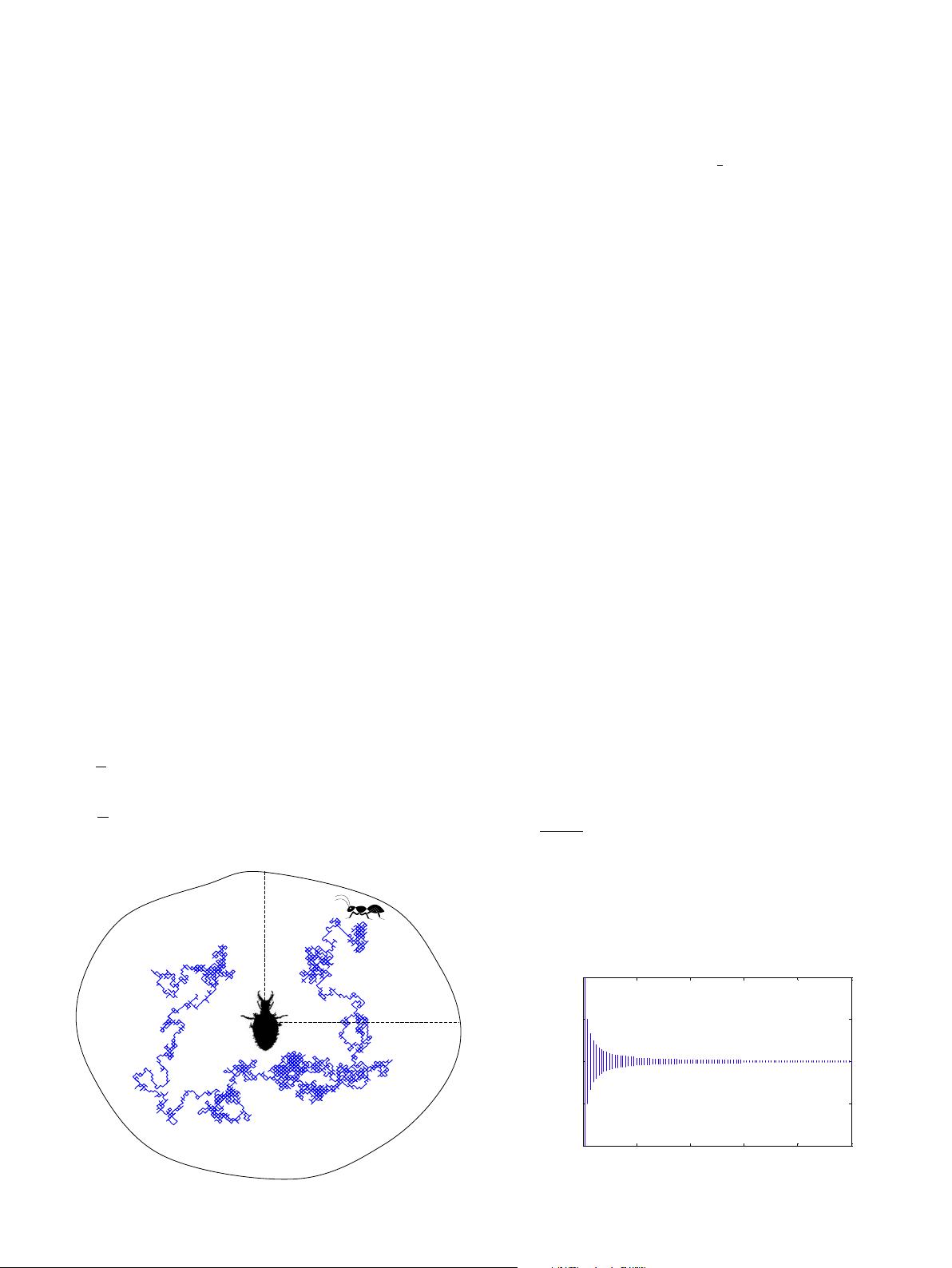
To have an image of this random walk, Fig. 2 is provided that

illustrates three random walks over 500 iterations. This ﬁgure

shows that the random walk utilized may ﬂuctuate dramatically

around the origin (red

curve), have increasing trend (black curve),

or have descending behaviour (blue curve).

The position of ants are saved and utilized during optimization

in the following matrix:

Ant

1;1

1;2

... ... A

1;d

2;1

2;2

... ... A

2;d

:::::

n;1

n;2

... ... A

n;d

ð2:3Þ

For interpretation of color in Fig. 2, the reader is referred to the web version of

this article.

S. Mirjalili / Advances in Engineering Software 83 (2015) 80–98

where M

Ant

is the matrix for saving the position of each ant, A

i,j

shows the value of the j-th variable (dimension) of i-th ant, n is

the number of ants, and d is the number of variables.

It should be noted that ants are similar to particles in PSO or

individuals in GA. The position of an ant refers the parameters

for a particular solution. Matrix M

Ant

has been considered to save

the position of all ants (variables of all solutions) during

optimization.

For evaluating each ant, a ﬁtness (objective) function is utilized

during optimization and the following matrix stores the ﬁtness

value of all ants:

f ½A

1;1;

1;2

; ...; A

1;d





f ½A

2;1

; A

2;2

; ...; A

2;d





f ½A

n;1

; A

n;2

; ...; A

n;d





ð2:4Þ

where M

is the matrix for saving the ﬁtness of each ant, A

i,j

shows

the value of j-th dimension of i-th ant, n is the number of ants, and f

is the objective function.

In addition to ants, we assume the antlions are also hiding

somewhere in the search space. In order save their positions and

ﬁtness values, the following matrices are utilized:

Antlion

1;1

1;2

... ... AL

1;d

2;1

2;2

... ... AL

2;d

:::::

n;1

n;2

... ... AL

n;d

ð2:5Þ

where M

Antlion

is the matrix for saving the position of each antlion,

i,j

shows the j-th dimension’s value of i-th antlion, n is the number

of antlions, and d is the number of variables (dimension).

OAL

f ð½AL

1;1;

1;2

; ...; AL

1;d

Þ

f ð½AL

2;1

; AL

2;2

; ...; AL

2;d

Þ

f ð½AL

n;1

; AL

n;2

; ...; AL

n;d

Þ

ð2:6Þ

where M

OAL

is the matrix for saving the ﬁtness of each antlion, AL

i,j

shows the j-th dimension’s value of i-th antlion, n is the number of

antlions, and f is the objective function.

During optimization, the following conditions are applied:

 Ants move around the search space using different random

walks.

 Random walks are applied to all the dimension of ants.

 Random walks are affected by the traps of antlions.

 Antlions can build pits proportional to their ﬁtness (the higher

ﬁtness, the larger pit).

 Antlions with larger pits have the higher probability to catch

ants.

 Each ant can be caught by an antlion in each iteration and the

elite (ﬁttest antlion).

 The range of random walk is decreased adaptively to simulate

sliding ants towards antlions.

 If an ant becomes ﬁtter than an antlion, this means that it is

caught and pulled under the sand by the antlion.

 An antlion repositions itself to the latest caught prey and builds

a pit to improve its change of catching another prey after each

hunt.

2.2.1. Random walks of ants

Random walks are all based on the Eq. (2.1). Ants update their

positions with random walk at every step of optimization. Since

every search space has a boundary (range of variable), however,

Eq. (2.1) cannot be directly used for updating position of ants.

In order to keep the random walks inside the search space, they

are normalized using the following equation (min–max

normalization):

 a



 d

 c



 a



þ c

ð2:7Þ

where a

is the minimum of random walk of i-th variable, b

is the

maximum of random walk in i-th variable, c

is the minimum of

i-th variable at t-th iteration, and d

indicates the maximum of

i-th variable at t-th iteration.

Eq. (2.7) should be applied in each iteration to guarantee the

occurrence of random walks inside the search space.

(a) (b)

Fig. 1. Cone-shaped traps and hunting behaviour of antlions.

0 100 200 300 400 500

-20

-10

X(t)

Fig. 2. Three random walks.

82 S. Mirjalili / Advances in Engineering Software 83 (2015) 80–98

2.2.2. Trapping in antlion’s pits

As discussed above, random walks of ants are affected by

antlions’ traps. In order to mathematically model this assumption,

the following equations are proposed:

¼ Antlion

þ c

ð2:8Þ

¼ Antlion

þ d

ð2:9Þ

where c

is the minimum of all variables at t-th iteration, d

indicates

the vector including the maximum of all variables at t-th iteration,

is the minimum of all variables for i-th ant, d

is the maximum of

all variables for i-th ant, and Antlion

shows the position of the

selected j-th antlion at t-th iteration.

Eqs. (2.8) and (2.9) show that ants randomly walk in a hyper

sphere deﬁned by the vectors c and d around a selected antlion.

A conceptual model of this behaviour is illustrated in Fig. 3.

Fig. 3 shows a two-dimensional search space. It may be

observed that ants are required to move within a hypersphere

around a selected antlion.

2.2.3. Building trap

In order to model the antlions’s hunting capability, a roulette

wheel is employed. As Fig. 3 show ants are assumed to be trapped

in only one selected antlion. The ALO algorithm is required to uti-

lize a roulette wheel operator for selecting antlions based of their

ﬁtness during optimization. This mechanism gives high chances

to the ﬁtter antlions for catching ants.

2.2.4. Sliding ants towards antlion

With the mechanisms proposed so far, antlions are able to build

traps proportional to their ﬁtness and ants are required to move

randomly. However, antlions shoot sands outwards the center of

the pit once they realize that an ant is in the trap. This behaviour

slides down the trapped ant that is trying to escape. For mathemat-

ically modelling this behaviour, the radius of ants’s random walks

hyper-sphere is decreased adaptively. The following equations are

proposed in this regard:

ð2:10Þ

ð2:11Þ

where I is a ratio, c

is the minimum of all variables at t-th iteration,

and d

indicates the vector including the maximum of all variables

at t-th iteration.

In Eqs. (2.10) and (2.11), I ¼ 10

where t is the current itera-

tion, T is the maximum number of iterations, and w is a constant

deﬁned based on the current iteration (w = 2 when t > 0.1T, w =3

when t > 0.5T, w = 4 when t > 0.75T, w = 5 when t > 0.9T, and

w = 6 when t > 0.95T). Basically, the constant w can adjust the

accuracy level of exploitation.

Fig. 4 also shows the decreasing behaviour using Eqs. (2.10) and

(2.11). These equations shrink the radius of updating ant’s

positions and mimics sliding process of ant inside the pits. This

guarantees exploitation of search space.

2.2.5. Catching prey and re-building the pit

The ﬁnal stage of hunt is when an ant reaches the bottom of the

pit and is caught in the antlion’s jaw. After this stage, the antlion

pulls the ant inside the sand and consumes its body. For mimicking

this process, it is assumed that catching prey occur when ants

becomes ﬁtter (goes inside sand) than its corresponding antlion.

An antlion is then required to update its position to the latest posi-

tion of the hunted ant to enhance its chance of catching new prey.

The following equation is proposed in this regard:

Antlion

¼ Ant

if f ðAnt

Þ > f Antlion



ð2:12Þ

where t shows the current iteration, Antlion

shows the position of

selected j-th antlion at t-th iteration, and Ant

indicates the position

of i-th ant at t-th iteration.

2.2.6. Elitism

Elitism is an important characteristic of evolutionary algo-

rithms that allows them to maintain the best solution(s) obtained

at any stage of optimization process. In this study the best antlion

obtained so far in each iteration is saved and considered as an elite.

Since the elite is the ﬁttest antlion, it should be able to affect the

movements of all the ants during iterations. Therefore, it is

assumed that every ant randomly walks around a selected antlion

by the roulette wheel and the elite simultaneously as follows:

Ant

þ R

ð2:13Þ

where R

is the random walk around the antlion selected by the

roulette wheel at t-th iteration, R

is the random walk around the

elite at t-th iteration, and Ant

indicates the position of i-th ant at

t-th iteration.

Fig. 3. Random walk of an ant inside an antlion’s trap.

0 20 40 60 80 100

-100

-50

100

Iteration (t)

lower bound (c) & upper bound (d)

Fig. 4. Adaptive lower (c

) and upper (d

) bounds.

S. Mirjalili / Advances in Engineering Software 83 (2015) 80–98

2.3. ALO algorithm

With the proposed operators in the preceding subsections, the

ALO optimization algorithm can now be deﬁned. The ALO algo-

rithm is deﬁned as a three-tuple function that approximates the

global optimum for optimization problems as follows:

ALOðA; B; CÞð2:14Þ

where A is a function that generates the random initial solutions, B

manipulates the initial population provided by the function A, and C

returns true when the end criterion is satisﬁed. The functions A, B,

and C are deﬁned as follows:

Ant

; M

Antlion

; M

OAL

gð2:15Þ

Ant

; M

Antlion

Ant

; M

Antlion

gð2:16Þ

Ant

; M

Antlion

ftrue; falsegð2:17Þ

where M

Ant

is the matrix of the position of ants, M

Antlion

includes the

position of antlions, M

contains the corresponding ﬁtness of ants,

and M

OAL

has the ﬁtness of antlions.

The pseudo codes the ALO algorithm are deﬁned as follows:

Initialize the ﬁrst population of ants and antlions randomly

Calculate the ﬁtness of ants and antlions

Find the best antlions and assume it as the elite (determined

optimum)

while the end criterion is not satisﬁed

for every ant

Select an antlion using Roulette wheel

Update c and d using equations Eqs. (2.10) and (2.11)

Create a random walk and normalize it using Eqs. (2.1) and

(2.7)

Update the position of ant using (2.13)

end for

Calculate the ﬁtness of all ants

Replace an antlion with its corresponding ant it if becomes

ﬁtter (Eq. (2.12))

Update elite if an antlion becomes ﬁtter than the elite

end while

Return elite

The Matlab codes for the overall framework of the ALO algo-

rithm as well as the functions A and B are provided in Appendix

A.1–A.3.

In the ALO algorithm, the antlion and ant matrices are initial-

ized randomly using the function A. In every iteration, the function

B updates the position of each ant with respect to an antlion

selected by the roulette wheel operator and the elite. The boundary

of position updating is ﬁrst deﬁned proportional to the current

number of iteration. The updating position is then accomplished

by two random walks around the selected antlion and elite. When

all the ants randomly walk, they are evaluated by the ﬁtness func-

tion. If any of the ants become ﬁtter than any other antlions, their

positions are considered as the new positions for the antlions in

the next iteration. The best antlion is compared to the best antlion

found during optimization (elite) and substituted if it is necessary.

These steps iterative until the function C returns false.

2.4. ALO software (toolbox)

The ALO algorithm is developed in Matlab and offered as an

open-source optimization toolbox. The main user interface of this

toolbox is illustrated in Fig. 5. The software designed allows users

to deﬁne the number of search agents, maximum number of itera-

tions, number of variables, upper bounds of variables, lower

bounds of variables, and the name of the objective function easily.

As shown in Fig. 5, these variables can be deﬁned in the ‘‘parame-

ters’’ section of the software. After deﬁning the parameters, the

problem starts to be optimized as soon as the user clicks on the

‘‘start optimization’’ button. The software then interactively draws

the convergence curve (and history if chosen) and updates the

obtained best optimum so far in the convergence curve section.

Eventually, the information of the best obtained optimum is shown

in the ‘‘ﬁnal results’’ section. Note that the source codes of the ALO

algorithm and the toolbox can be downloaded from http://www.

alimirjalili.com/ALO.html or http://www.mathworks.com/matlab-

central/proﬁle/authors/2943818-seyedali-mirjalili.

2.5. Hypotheses about the ALO algorithm

Theoretically speaking, the proposed ALO algorithm is able to

approximate the global optimum of optimization problems due

to the following reasons:

 Exploration of the search space is guaranteed by the random

selection of antlions and random walks of ants around them.

 Exploitation of search space is guaranteed by the adaptive

shrinking boundaries of antlions’ traps.

 There is high probability of resolving local optima stagnation

due to the use of random walks and the roulette wheel.

 ALO is a population-based algorithm, so local optima avoidance

is intrinsically high.

 Intensity of ants’ movement is adaptively decreased over the

course of iterations, which guarantees convergence of the ALO

algorithm.

 Calculating random walks for every ant and every dimension

promotes diversity in the population.

 Antlions relocate to the position of best ants during optimiza-

tion, so promising areas of search spaces are saved.

 Antlions guide ants towards promising regions of the search

space.

 The best antlion in each iteration is saved and compared to the

best antlion obtained so far (elite).

 The ALO algorithm has very few parameters to adjust.

 The ALO algorithm is a gradient-free algorithm and considers

problem as a black box.

In the next sections several test beds and real problems are

employed to benchmark and conﬁrm the performance of the ALO

algorithm in solving optimization problems.

3. Results and discussion

In this section a number of test problems are selected to bench-

mark the performance of the proposed ALO algorithm. Three

groups of test functions are employed with different characteristics

to test the performance of the ALO algorithm from different

perspectives. The test functions are divided the three groups: uni-

modal (Table 1), multi-modal (Table 2), and composite functions

(Table 3) [20,56–58]. As their names imply, unimodal test func-

tions have single optimum so they can benchmark the exploitation

and convergence of an algorithm. In contrast, multi-modal test

functions have more than one optimum, making them more chal-

lenging than unimodal functions. One of the optima is called global

optimum and the rest are called local optima. An algorithm should

avoid all the local optima to approach and determine the global

optimum. Therefore, exploration and local optima avoidance of

84 S. Mirjalili / Advances in Engineering Software 83 (2015) 80–98

评论收藏

内容反馈

版权申诉

依然风yrlf

粉丝: 1530
资源: 3116

基于matlab实现蚁狮优化算法

蚁狮优化算法（matlab）

混沌蚁狮优化器：这段代码实现了蚁狮优化器的混沌版本。-matlab开发

蚁群优化算法优化连续域上Ackley基准函数（matlab实现）。

【蚁狮算法】基于具有自适应边界与最优引导的莱维飞行蚁狮优化算法（ABLALO）求解单目标优化问题matlab代码.zip

多目标蚂蚁狮子优化算法（MOALO）（Matlab代码实现）.zip

【JCR2区】Matlab实现蚁狮优化算法ALO-LSSVM实现数据分类算法研究.rar

基于matlab编程实现的蚁狮优化算法.rar

【优化求解】基于优选策略的自适应蚁狮优化算法matlab源码.md

【优化算法】蚁狮优化算法(ALO)【含Matlab源码 1307期】.zip

【蚁狮算法】基于柯西变异的蚁狮优化算法求解单目标优化问题matlab代码.zip

基于Matlab

【3】The Ant Lion Optimizer-蚁狮群优化算法附matlab代码.zip

蚁群优化算法的matlab代码

多目标蚂蚁狮子优化算法（MOALO）（Matlab代码实现）.zip.zip

基于MatlabMatlab

蚁狮优化算法Matlab

蚁狮优化算法深度解析与应用场景(文档加Matlab源码)

【中科院1区】Matlab实现蚁狮优化算法ALO-SAE实现故障诊断算法研究.rar

【独家首发】Matlab实现蚁狮优化算法ALO优化Transformer-LSTM实现负荷数据回归预测.rar

蚁狮算法(Ant Lion Algorithm）Python实现和matlab实现

基于matlab实现的改进的蚂蚁算法，即带精英策略的蚂蚁算法，求解TSP问题 对深入理解蚂蚁算法的优化原理很有帮助 .rar

施肥优化算法（matlab实现）

【优化调度】基于蚁狮算法求解经济调度问题附matlab代码+仿真结果和运行方法+仿真结果和运行方法.zip

【SVM分类】基于自适应蚁狮算法优化SVM分类器实现胃肠道病变附matlab代码.zip

自适应蚁群优化算法

【JCR一区级】Matlab实现蚁狮优化算法ALO-DBN实现轴承故障分类算法研究.rar

【创新未发表】Matlab实现蚁狮优化算法ALO-GRU实现风电数据预测算法研究.rar

【布局优化】基于蚁狮算法的无线传感器网(WSN)覆盖优化matlab源码.zip

【独家首发】Matlab实现蚁狮优化算法ALO优化Transformer-BiLSTM实现负荷数据回归预测.rar

Matlab实现蚁狮优化算法ALO-CNN-LSTM-Multihead-Attention温度预测.rar

最新资源

基于matlab实现的改进的蚂蚁算法，即带精英策略的蚂蚁算法，求解TSP问题对深入理解蚂蚁算法的优化原理很有帮助 .rar