ADistributionalPerspectiveonReinforcementLearning.pdf资源-CSDN文库

Distributional

需积分: 31 62 浏览量 2019-09-02 11:29:40 上传评论收藏 1.63MB PDF 举报

资源推荐

资源详情

资源评论

A Distributional Perspective on Reinforcement Learning

Marc G. Bellemare

* 1

Will Dabney

* 1

emi Munos

Abstract

In this paper we argue for the fundamental impor-

tance of the value distribution: the distribution

of the random return received by a reinforcement

learning agent. This is in contrast to the com-

mon approach to reinforcement learning which

models the expectation of this return, or value.

Although there is an established body of liter-

ature studying the value distribution, thus far it

has always been used for a speciﬁc purpose such

as implementing risk-aware behaviour. We begin

with theoretical results in both the policy eval-

uation and control settings, exposing a signiﬁ-

cant distributional instability in the latter. We

then use the distributional perspective to design

a new algorithm which applies Bellman’s equa-

tion to the learning of approximate value distri-

butions. We evaluate our algorithm using the

suite of games from the Arcade Learning En-

vironment. We obtain both state-of-the-art re-

sults and anecdotal evidence demonstrating the

importance of the value distribution in approxi-

mate reinforcement learning. Finally, we com-

bine theoretical and empirical evidence to high-

light the ways in which the value distribution im-

pacts learning in the approximate setting.

1. Introduction

One of the major tenets of reinforcement learning states

that, when not otherwise constrained in its behaviour, an

agent should aim to maximize its expected utility Q, or

value (Sutton & Barto, 1998). Bellman’s equation succintly

describes this value in terms of the expected reward and ex-

pected outcome of the random transition (x, a) →(X

, A

Q(x, a) = E R(x, a) + γ E Q(X

, A

In this paper, we aim to go beyond the notion of value and

argue in favour of a distributional perspective on reinforce-

Equal contribution

DeepMind, London, UK. Correspon-

dence to: Marc G. Bellemare <bellemare@google.com>.

Proceedings of the 34

International Conference on Machine

by the author(s).

ment learning. Speciﬁcally, the main object of our study is

the random return Z whose expectation is the value Q. This

random return is also described by a recursive equation, but

one of a distributional nature:

Z(x, a)

= R(x, a) + γZ(X

, A

The distributional Bellman equation states that the distribu-

tion of Z is characterized by the interaction of three random

variables: the reward R, the next state-action (X

, A

), and

its random return Z(X

, A

). By analogy with the well-

known case, we call this quantity the value distribution.

Although the distributional perspective is almost as old

as Bellman’s equation itself (Jaquette, 1973; Sobel, 1982;

White, 1988), in reinforcement learning it has thus far been

subordinated to speciﬁc purposes: to model parametric un-

certainty (Dearden et al., 1998), to design risk-sensitive al-

gorithms (Morimura et al., 2010b;a), or for theoretical anal-

ysis (Azar et al., 2012; Lattimore & Hutter, 2012). By con-

trast, we believe the value distribution has a central role to

play in reinforcement learning.

Contraction of the policy evaluation Bellman operator.

Basing ourselves on results by R

osler (1992) we show that,

for a ﬁxed policy, the Bellman operator over value distribu-

tions is a contraction in a maximal form of the Wasserstein

(also called Kantorovich or Mallows) metric. Our partic-

ular choice of metric matters: the same operator is not a

contraction in total variation, Kullback-Leibler divergence,

or Kolmogorov distance.

Instability in the control setting. We will demonstrate an

instability in the distributional version of Bellman’s opti-

mality equation, in contrast to the policy evaluation case.

Speciﬁcally, although the optimality operator is a contrac-

tion in expected value (matching the usual optimality re-

sult), it is not a contraction in any metric over distributions.

These results provide evidence in favour of learning algo-

rithms that model the effects of nonstationary policies.

Better approximations. From an algorithmic standpoint,

there are many beneﬁts to learning an approximate distribu-

tion rather than its approximate expectation. The distribu-

tional Bellman operator preserves multimodality in value

distributions, which we believe leads to more stable learn-

ing. Approximating the full distribution also mitigates the

effects of learning from a nonstationary policy. As a whole,

arXiv:1707.06887v1 [cs.LG] 21 Jul 2017

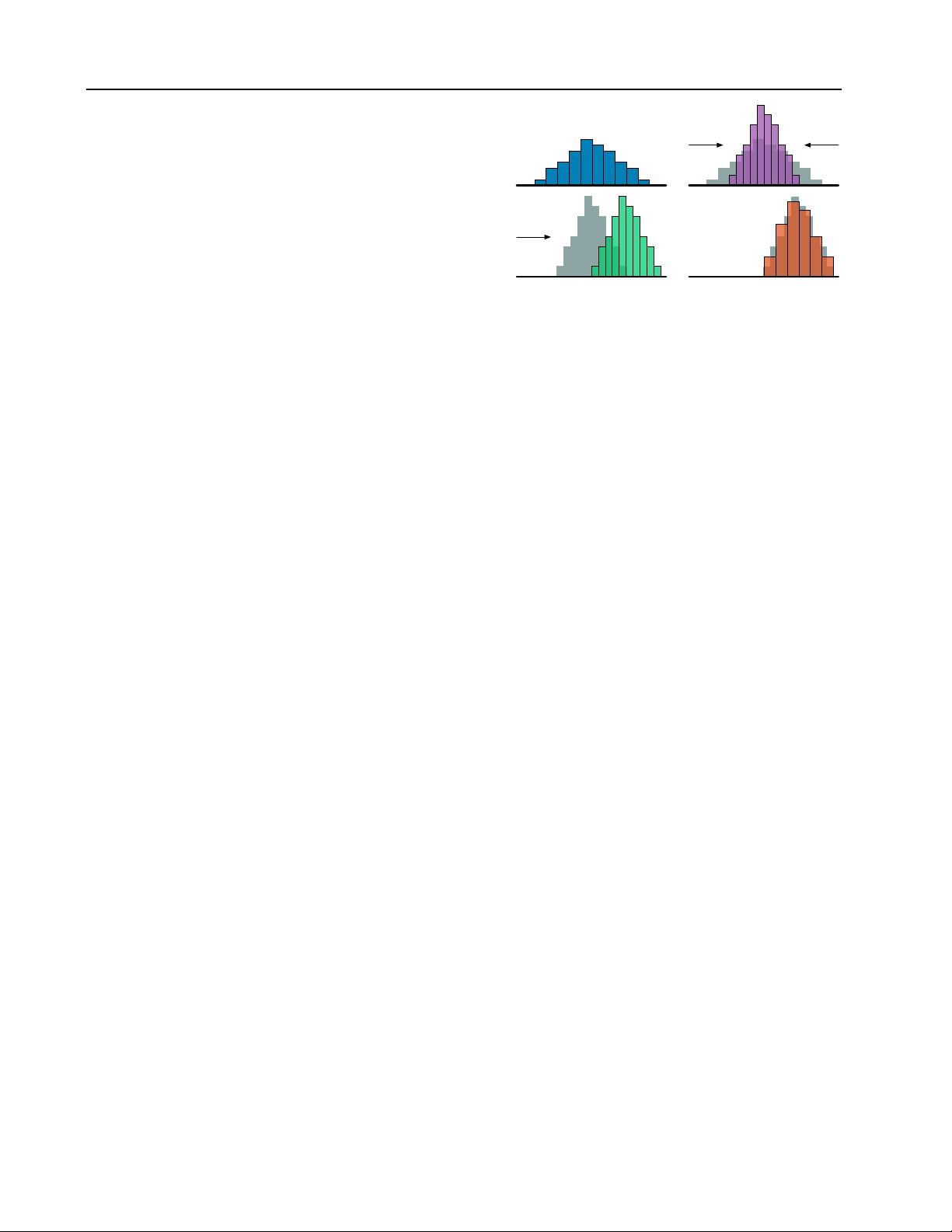
A Distributional Perspective on Reinforcement Learning

we argue that this approach makes approximate reinforce-

ment learning signiﬁcantly better behaved.

We will illustrate the practical beneﬁts of the distributional

perspective in the context of the Arcade Learning Environ-

ment (Bellemare et al., 2013). By modelling the value dis-

tribution within a DQN agent (Mnih et al., 2015), we ob-

tain considerably increased performance across the gamut

of benchmark Atari 2600 games, and in fact achieve state-

of-the-art performance on a number of games. Our results

echo those of Veness et al. (2015), who obtained extremely

fast learning by predicting Monte Carlo returns.

From a supervised learning perspective, learning the full

value distribution might seem obvious: why restrict our-

selves to the mean? The main distinction, of course, is that

in our setting there are no given targets. Instead, we use

Bellman’s equation to make the learning process tractable;

we must, as Sutton & Barto (1998) put it, “learn a guess

from a guess”. It is our belief that this guesswork ultimately

carries more beneﬁts than costs.

2. Setting

We consider an agent interacting with an environment in

the standard fashion: at each step, the agent selects an ac-

tion based on its current state, to which the environment re-

sponds with a reward and the next state. We model this in-

teraction as a time-homogeneous Markov Decision Process

(X, A, R, P, γ). As usual, X and A are respectively the

state and action spaces, P is the transition kernel P (·|x, a),

γ ∈ [0, 1] is the discount factor, and R is the reward func-

tion, which in this work we explicitly treat as a random

variable. A stationary policy π maps each state x ∈ X to a

probability distribution over the action space A.

2.1. Bellman’s Equations

The return Z

is the sum of discounted rewards along the

agent’s trajectory of interactions with the environment. The

value function Q

of a policy π describes the expected re-

turn from taking action a ∈ A from state x ∈ X, then

acting according to π:

(x, a) := E Z

(x, a) = E

∞

t=0

R(x

, a

)

, (1)

∼ P (·|x

t−1

, a

t−1

), a

∼ π(·|x

), x

= x, a

= a.

Fundamental to reinforcement learning is the use of Bell-

man’s equation (Bellman, 1957) to describe the value func-

tion:

(x, a) = E R(x, a) + γ E

P,π

, a

In reinforcement learning we are typically interested in act-

ing so as to maximize the return. The most common ap-

P

⇡

R+

⇡



⇡

(a) (b)

⇡



Figure 1. A distributional Bellman operator with a deterministic

reward function: (a) Next state distribution under policy π, (b)

Discounting shrinks the distribution towards 0, (c) The reward

shifts it, and (d) Projection step (Section 4).

proach for doing so involves the optimality equation

∗

(x, a) = E R(x, a) + γ E

max

∈A

∗

, a

This equation has a unique ﬁxed point Q

∗

, the optimal

value function, corresponding to the set of optimal policies

∗

(π

∗

is optimal if E

a∼π

∗

(x, a) = max

∗

(x, a)).

We view value functions as vectors in R

X ×A

, and the ex-

pected reward function as one such vector. In this context,

the Bellman operator T

and optimality operator T are

Q(x, a) := E R(x, a) + γ E

P,π

Q(x

, a

) (2)

T Q(x, a) := E R(x, a) + γ E

max

∈A

Q(x

, a

). (3)

These operators are useful as they describe the expected

behaviour of popular learning algorithms such as SARSA

and Q-Learning. In particular they are both contraction

mappings, and their repeated application to some initial Q

converges exponentially to Q

or Q

∗

, respectively (Bert-

sekas & Tsitsiklis, 1996).

3. The Distributional Bellman Operators

In this paper we take away the expectations inside Bell-

man’s equations and consider instead the full distribution

of the random variable Z

. From here on, we will view Z

as a mapping from state-action pairs to distributions over

returns, and call it the value distribution.

Our ﬁrst aim is to gain an understanding of the theoretical

behaviour of the distributional analogues of the Bellman

operators, in particular in the less well-understood control

setting. The reader strictly interested in the algorithmic

contribution may choose to skip this section.

3.1. Distributional Equations

It will sometimes be convenient to make use of the proba-

bility space (Ω, F, Pr). The reader unfamiliar with mea-

A Distributional Perspective on Reinforcement Learning

sure theory may think of Ω as the space of all possible

outcomes of an experiment (Billingsley, 1995). We will

write kuk

to denote the L

norm of a vector u ∈ R

for

1 ≤ p ≤ ∞; the same applies to vectors in R

X ×A

. The

norm of a random vector U : Ω → R

(or R

X ×A

) is

then kU k



kU(ω)k



1/p

, and for p = ∞ we have

kUk

∞

= ess sup kU(ω)k

∞

(we will omit the dependency

on ω ∈ Ω whenever unambiguous). We will denote the

c.d.f. of a random variable U by F

(y) := Pr{U ≤ y},

and its inverse c.d.f. by F

−1

(q) := inf{y : F

(y) ≥ q}.

A distributional equation U

:= V indicates that the ran-

dom variable U is distributed according to the same law

as V . Without loss of generality, the reader can understand

the two sides of a distributional equation as relating the dis-

tributions of two independent random variables. Distribu-

tional equations have been used in reinforcement learning

by Engel et al. (2005); Morimura et al. (2010a) among oth-

ers, and in operations research by White (1988).

3.2. The Wasserstein Metric

The main tool for our analysis is the Wasserstein metric d

between cumulative distribution functions (see e.g. Bickel

& Freedman, 1981, where it is called the Mallows metric).

For F, G two c.d.fs over the reals, it is deﬁned as

(F, G) := inf

U,V

kU −V k

where the inﬁmum is taken over all pairs of random vari-

ables (U, V ) with respective cumulative distributions F

and G. The inﬁmum is attained by the inverse c.d.f. trans-

form of a random variable U uniformly distributed on [0, 1]:

(F, G) = kF

−1

(U) − G

−1

(U)k

For p < ∞ this is more explicitly written as

(F, G) =





−1

(u) − G

−1

(u)





1/p

Given two random variables U, V with c.d.fs F

, F

, we

will write d

(U, V ) := d

, F

). We will ﬁnd it conve-

nient to conﬂate the random variables under consideration

with their versions under the inf, writing

(U, V ) = inf

U,V

kU −V k

whenever unambiguous; we believe the greater legibility

justiﬁes the technical inaccuracy. Finally, we extend this

metric to vectors of random variables, such as value distri-

butions, using the corresponding L

norm.

Consider a scalar a and a random variable A independent

of U, V . The metric d

has the following properties:

(aU, aV ) ≤ |a|d

(U, V ) (P1)

(A + U, A + V ) ≤ d

(U, V ) (P2)

(AU, AV ) ≤ kAk

(U, V ). (P3)

We will need the following additional property, which

makes no independence assumptions on its variables. Its

proof, and that of later results, is given in the appendix.

Lemma 1 (Partition lemma). Let A

, A

, . . . be a set of

random variables describing a partition of Ω, i.e. A

(ω) ∈

{0, 1} and for any ω there is exactly one A

with A

(ω) =

1. Let U, V be two random variables. Then



U, V



≤

U, A

V ).

Let Z denote the space of value distributions with bounded

moments. For two value distributions Z

, Z

∈ Z we will

make use of a maximal form of the Wasserstein metric:

, Z

) := sup

x,a

(x, a), Z

(x, a)).

We will use

to establish the convergence of the distribu-

tional Bellman operators.

Lemma 2.

is a metric over value distributions.

3.3. Policy Evaluation

In the policy evaluation setting (Sutton & Barto, 1998) we

are interested in the value function V

associated with a

given policy π. The analogue here is the value distribu-

tion Z

. In this section we characterize Z

and study the

behaviour of the policy evaluation operator T

. We em-

phasize that Z

describes the intrinsic randomness of the

agent’s interactions with its environment, rather than some

measure of uncertainty about the environment itself.

We view the reward function as a random vector R ∈ Z,

and deﬁne the transition operator P

: Z → Z

Z(x, a)

:= Z(X

, A

) (4)

∼ P (·|x, a), A

∼ π(·|X

where we use capital letters to emphasize the random na-

ture of the next state-action pair (X

, A

). We deﬁne the

distributional Bellman operator T

: Z → Z as

Z(x, a)

:= R(x, a) + γP

Z(x, a). (5)

While T

bears a surface resemblance to the usual Bell-

man operator (2), it is fundamentally different. In particu-

lar, three sources of randomness deﬁne the compound dis-

tribution T

剩余18页未读，继续阅读

评论收藏

内容反馈

GanD.GanD

粉丝: 3
资源: 90

A Distributional Perspective on Reinforcement Learning.pdf

最新资源

A Distributional Perspective on Reinforcement Learning.pdf

Distributional Reinforcement Learning with Quantile Regression.pdf

8.quantile regression dqn.ipynb

6.categorical dqn.ipynb

Reinforcement Learning.pdf

A Tour of Reinforcement Learning.pdf

Reinforcement Learning--A Survey.pdf

An Introduction to Reinforcement Learning.pdf

An Introduction to Deep Reinforcement Learning.pdf

Reinforcement Learning An Introduction2019.pdf.zip

Word Segmentation:The Role of Distributional Cues.pdf

An Introduction to DRL.pdf

Text Mining: Classification, Clustering, and Applications

Multi-Agent Reinforcement Learning.pdf

An_introduction_to_Reinforcement_Learning.pdf

04_Word_Similarity-_Distributional_Similarity_I_13-14.pdf

BatchNorm有效性原理探索.pdf

保守离线分布强化学习_Conservative Offline Distributional Reinforcement Lea

05_Word_Similarity-_Distributional_Similarity_II_8-15.pdf

Knowledge Graphs and Language Technology

Reinforcement Learning An Introduction.pdf

Machine Learning A Probabilistic Perspective.pdf

Reinforcement Learning-Theory and Algorithm.pdf

Reinforcement Learning：An Introduction.pdf

Distributional Semantics Approach of Named Entities

Distrubutional Similarity vs. PU Learning for Entity Set Expansion论文PPT

最新资源