图解迪杰斯特拉（Dijkstra）最短路径算法.docx

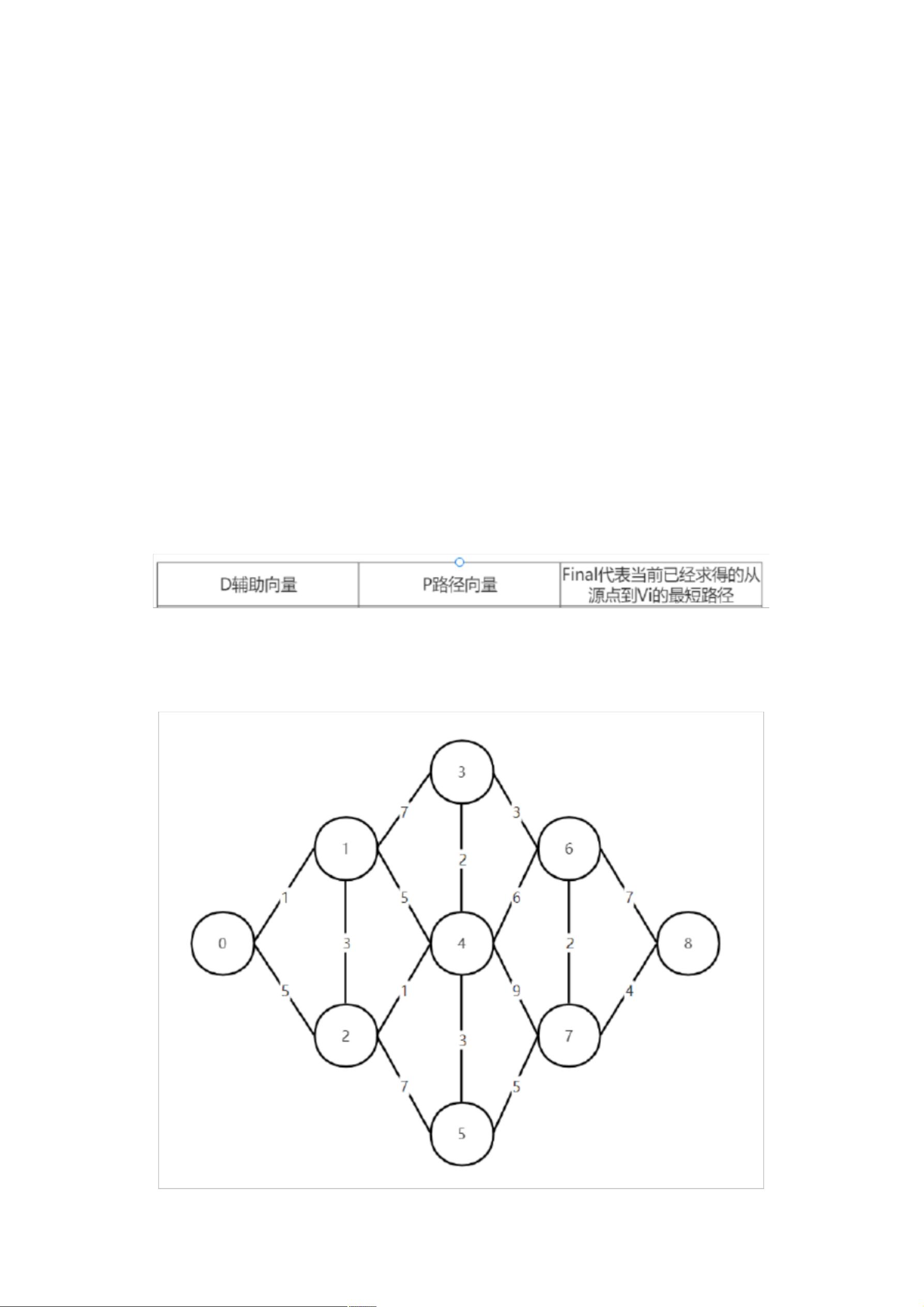
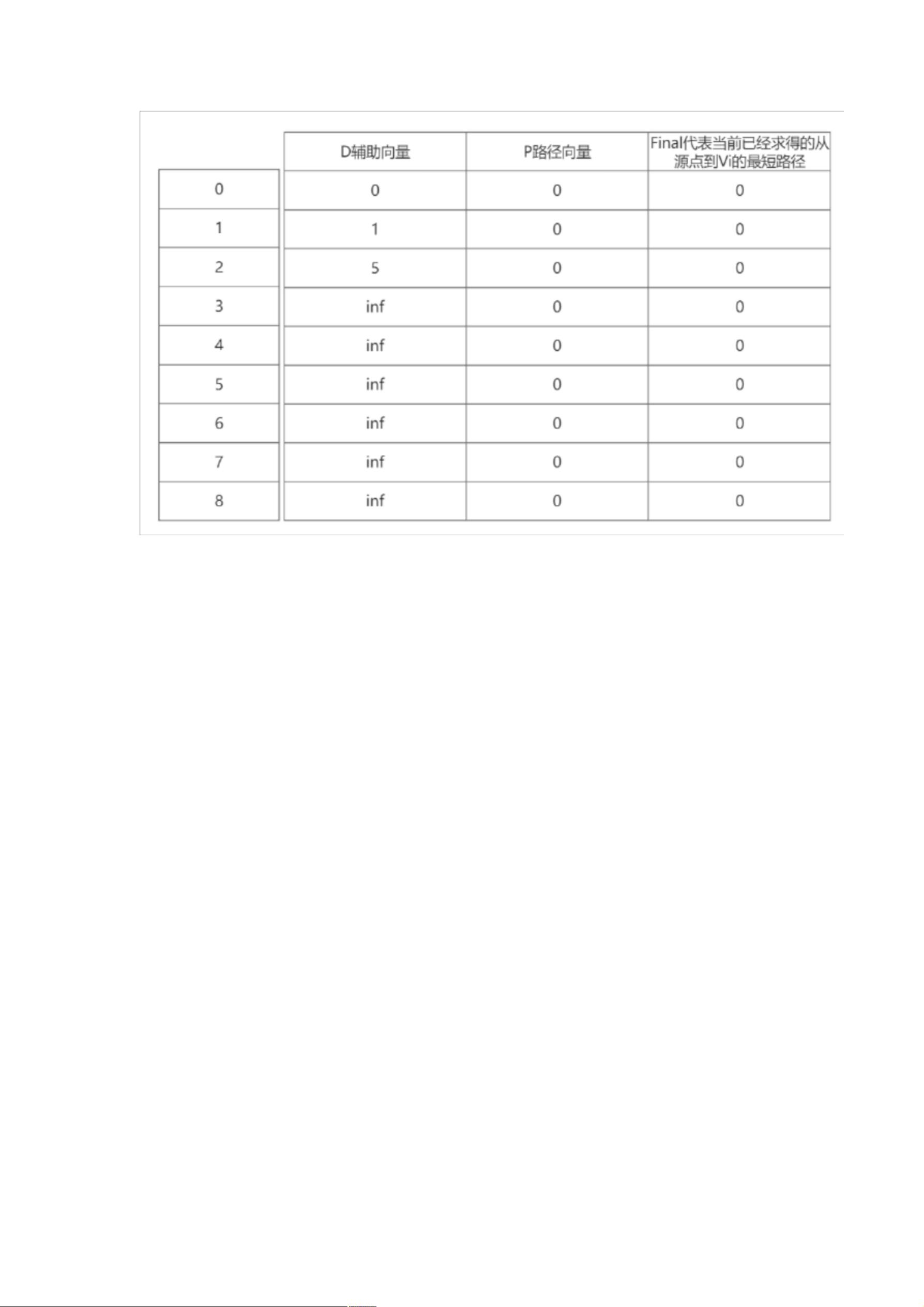
一、最短路径的概念及应用 在介绍最短路径之前我们首先要明白两个概念：什么是源点，什么是终点？在一条路径中，起始的第 一个节点叫做源点；终点：在一条路径中，最后一个的节点叫做终点；注意！源点和终点都只是相对 于一条路径而言，每一条路径都会有相同或者不相同的源点和终点。 而最短路径这个词不用过多解释，就是其字面意思： 在图中，对于非带权无向图而言， 从源点到终点 边最少的路径（也就是 BFS 广度优先的方法）； 而对于带权图而言， 从源点到终点权值之和最少的 路径叫最短路径； 最短路径应用：道路规划； 我们最关心的就是如何用代码去实现寻找最短路径， 通过实现最短路径有两种算法：Dijkstra 迪杰斯 特拉算法和 Floyd 弗洛伊德算法， 接下来我会详细讲解 Dijkstra 迪杰斯特拉算法； ### 图解迪杰斯特拉（Dijkstra）最短路径算法 #### 一、最短路径的概念及应用 在深入探讨迪杰斯特拉算法之前，有必要先理解“最短路径”的基本概念及其应用场景。 ##### 1. **源点与终点** 在任意路径中，**源点**是指路径的起点，而**终点**则是路径的结束点。这两个概念是相对的，不同的路径可能会有不同的源点和终点。 ##### 2. **最短路径定义** 最短路径是指在一个图中，从源点到终点之间所有可能路径中边数最少或权值之和最小的那条路径。对于非带权图（即图中的边没有权重），最短路径通常是指边数最少的路径，这可以通过广度优先搜索（BFS）算法来实现。而对于带权图（即图中的边具有权重），最短路径是指权值之和最小的路径。 ##### 3. **应用场景** 最短路径的应用非常广泛，尤其是在道路规划领域。例如，在GPS导航系统中，最短路径算法被用来计算从出发点到目的地的最佳行驶路线，以确保行程时间和距离最短。 #### 二、迪杰斯特拉算法详解 迪杰斯特拉算法是由荷兰计算机科学家Edsger W. Dijkstra于1956年提出的，用于求解单源点最短路径问题。该算法适用于带权图，且假设图中不存在负权边。 ##### 1. **迪杰斯特拉算法简介** 迪杰斯特拉算法的核心思想是逐步扩展从源点到其他各点的最短路径集合。初始时，只有源点被认为是最短路径的一部分。然后，算法不断选择当前未确定最短路径的顶点中距离源点最近的一个顶点，并更新从源点到该顶点的最短路径以及与该顶点相邻的所有顶点的距离估计值。这个过程一直持续到所有顶点都被访问过。 ##### 2. **逻辑实现** 为了更好地理解迪杰斯特拉算法的工作原理，下面通过一个具体的例子来详细介绍其逻辑实现。 **准备工作** - **初始化辅助数组** - **D** 数组用于记录从源点到各个顶点的当前已知最短距离。 - **P** 数组用于记录从源点到达某个顶点的前一个顶点。 - **Final** 数组用于标记某个顶点是否已经被包含在最终的最短路径中。 **算法步骤** 1. **初始化** - 将源点到自身的距离设为0，其余顶点到源点的距离设为无穷大。 - 所有顶点的Final值初始化为0。 2. **选取下一个顶点** - 从未被Final标记的顶点中选取距离源点最短的那个顶点u，并将其Final标记设为1。 3. **更新距离** - 对于顶点u的每个邻接顶点v，检查从源点经过u到达v的路径是否比当前记录的从源点到v的路径更短。 - 如果更短，则更新v的最短距离和前驱顶点。 4. **重复步骤2和3** - 直到所有顶点都被Final标记为止。 **示例分析** 假设我们有一个带权无向图，其中包含9个顶点V0至V8，我们想要找出从V0到V8的最短路径。 - **初始化阶段** - D数组中，与V0相连的顶点V1和V2的距离分别初始化为1和5，其余顶点设为无穷大。 - P数组中，对于V0到V1的路径前驱顶点为V0，其余顶点设为-1（表示未知）。 - Final数组中所有顶点均设为0。 - **第一次迭代** - 从V0出发，选择距离最近的顶点V1加入Final，并更新D和P数组。 - 由于V1的存在，从V0到V2的距离变为4（V0->V1->V2），因此更新D[2]为4，P[2]为1。 - **后续迭代** - 持续迭代，每次选择距离源点最近的未Final顶点，更新D和P数组。 - 直到最后一个顶点V8被加入Final，完成整个算法。 通过这种方式，迪杰斯特拉算法能够有效地找出从源点到所有其他顶点的最短路径。需要注意的是，该算法仅适用于没有负权边的情况。如果存在负权边，则需要考虑使用其他算法，比如贝尔曼-福特算法。