没有合适的资源?快使用搜索试试~ 我知道了~
温馨提示
内容概要:本文详细介绍了运算放大器固有噪声的分析与测量方法,包括热噪声和1/f噪声的基本概念及其计算方法。通过具体的计算实例,文章展示了如何利用SPICE仿真器和示波器等工具对运算放大器电路的噪声进行精确测量。文章强调了噪声带宽的概念,解释了不同类型滤波器的影响,并讨论了频谱分析仪的应用。 适合人群:电子工程师,尤其是从事模拟电路设计和技术支持的专业人士。 使用场景及目标:本文旨在帮助工程师掌握运算放大器噪声的分析与测量技巧,提高电路设计的精度和可靠性。具体应用场景包括精密测量系统、音频系统和信号处理等领域。 阅读建议:文章内容较为复杂,涉及大量的公式和图表。建议读者先理解基本的电路噪声理论,再逐步深入具体的计算步骤和测量方法。
资源推荐
资源详情
资源评论
运算放大器电路中固有噪声的分析与测量
第一部分:引言与统计数据评论
作者:德州仪器公司高级应用工程师 Art Kay
我们可将噪声定义为电子系统中任何不需要的信号。噪声会导致音频信号质量下降
以及精确测量方面的错误。板级与系统级电子设计工程师希望能确定其设计方案在
最差条件下的噪声到底有多大,并找到降低噪声的方法以及准确确认其设计方案可
行性的测量技术。
噪声包括固有噪声及外部噪声,这两种基本类型的噪声均会影响电子电路的性能。
外部噪声来自外部噪声源,典型例子包括数字交换、60Hz 噪声以及电源交换等。
固有噪声由电路元件本身生成,最常见的例子包括宽带噪声、热噪声以及闪烁噪声
等。本系列文章将介绍如何通过计算来预测电路的固有噪声大小,如何采用 SPICE
模拟技术,以及噪声测量技术等。
热噪声
热噪声由导体中电子的不规则运动而产生。由于运动会升高温度,因此热噪声的幅
度会随温度的上升而提高。我们可将热噪声视为组件(如电阻器)电压的不规则变
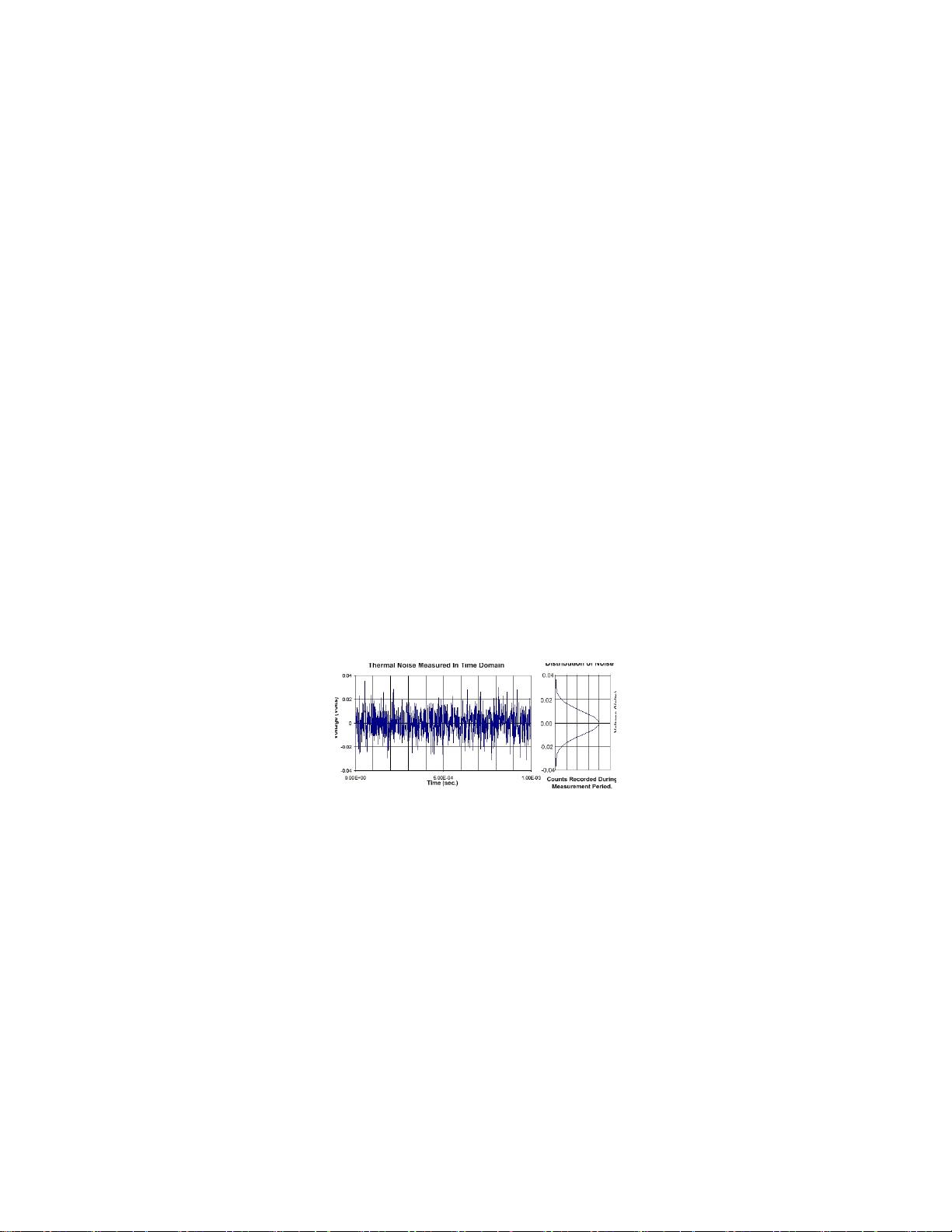
化。图 1.1 显示了标准示波器测得的一定时间域中热噪声波形,我们从图中还可看
到,如果从统计学的角度来分析随机信号的话,那么它可表现为高斯分布曲线。我
们给出分布曲线的侧面图,从中可以看出它与时间域信号之间的关系。
图 1.1: 在时间域中显示白噪声以及统计学分析结果
热噪声信号所包含的功率与温度及带宽直接成正比。请注意,我们可简单应用功率
方程式来表达电压与电阻之间的关系 (见方程式 1.1),根据该表达式,我们可以
估算出电路均方根 (RMS) 噪声的大小。此外,它还说明了在低噪声电路中尽可能
采用低电阻元件的重要性。

e
n
4kTR∆f
where e is the rms noise voltage
T is Temperature in Kelvin (K)
R is Resistance in Ohms (
Ω
)
f is noise bandiwdth frequency in Hertz (Hz)
k is Boltzmann's Constant 1.381E-23 joule/K
Note to convert degrees Celsius to Kelvin
T
K
= 273.15
o
C + T
C
方程式 1.1:热电压
方程式 1.1 中有一点值得重视的是,根据该表达式我们还可计算出 RMS 噪声电
压。在大多数情况下,工程师希望了解“最差条件下噪声会有多严重?”换言之,
他们非常关心峰值对峰值电压的情况。如果我们要将 RMS 热噪声电压转化为峰值
对峰值噪声的话,那么必须记住的一点是:噪声会表现为高斯分布曲线。这里有一
些单凭经验的方法即根据统计学上的关系,我们可将 RMS 热噪声电压转化为峰值
对峰值噪声。不过,在介绍有关方法前,我想先谈谈一些数学方面的基本原理。本
文的重点在于介绍统计学方面的基本理论,随后几篇文章将讨论实际模拟电路的测
量与分析事宜。
概率密度函数:
构成正态分布函数的数学方程式称作“概率密度函数”(见方程式 1.2)。根据一
段时间内测得的噪声电压绘制出相应的柱状图,从该柱状图,我们可以大致看出函
数所表达的形状。图 1.2 显示了测得的噪声柱状图,并给出了相应的概率密度函
数。
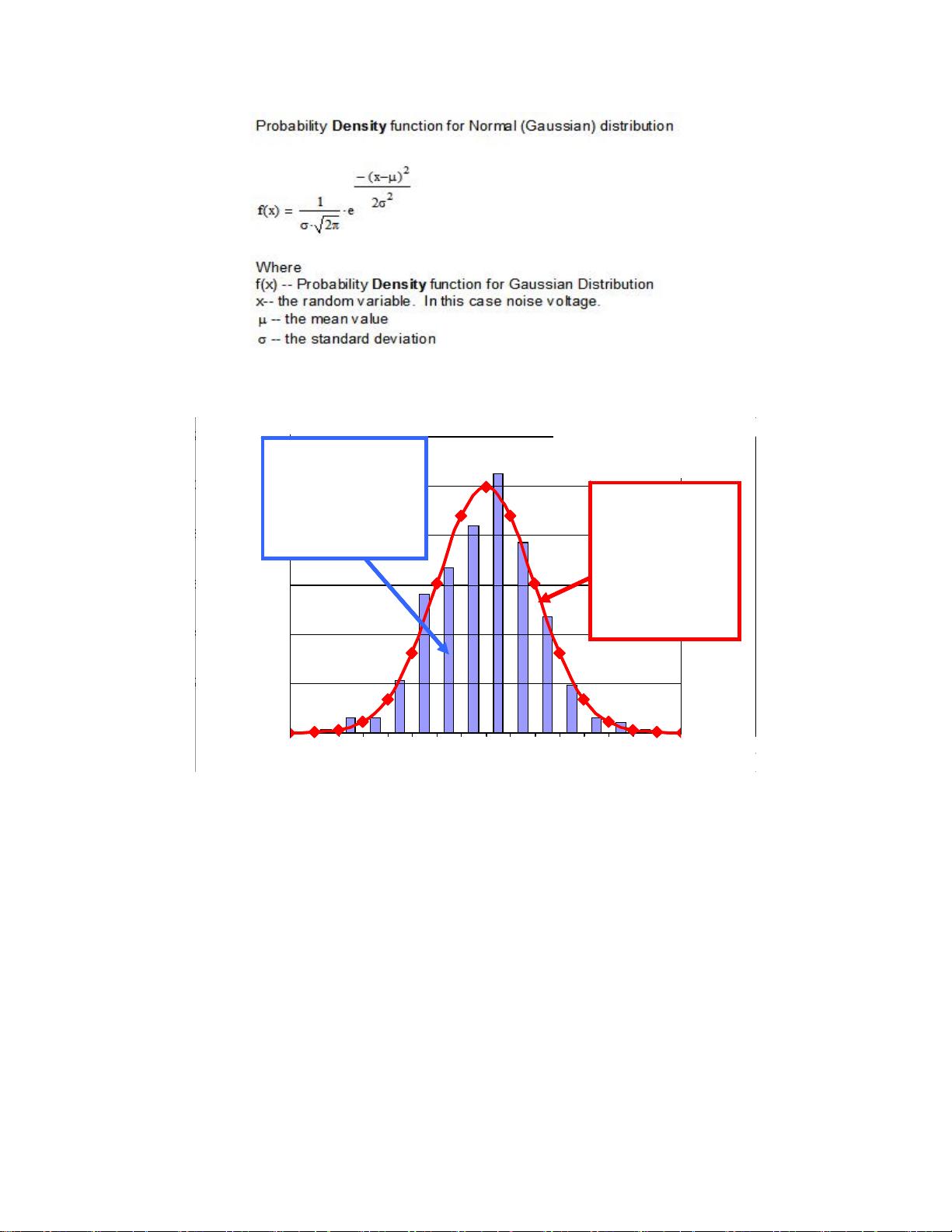
方程式 1.2: 高斯曲线分布曲线对应的概率密度函数
0
2
0
4
0
6
0
8
0
0
0
2
0
-5
-4.5
-4
-3
.5
-3
-2.5
-2
-1
.5
-
1
-0
.
5
0
0.5
1
1
.5
2
2.5
3
3
.5
4
4.5
5
Mo
re
0
20
40
60
80
100
120
-5.5 -5 -4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5
.
Sampled data
plotted in
histogram
format.
Instantaneous Voltage Amplitude
-2 -1 0 1 2
Number of Counts
for sampled data
Probability
Density Function
0
2
0
4
0
6
0
8
0
0
0
2
0
-5
-4.5
-4
-3
.5
-3
-2.5
-2
-1
.5
-
1
-0
.
5
0
0.5
1
1
.5
2
2.5
3
3
.5
4
4.5
5
Mo
re
0
20
40
60
80
100
120
-5.5 -5 -4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 5
.
Sampled data
plotted in
histogram
format.
Instantaneous Voltage Amplitude
-2 -1 0 1 2
Number of Counts
for sampled data
Probability
Density Function
图 1.2: 根据相应的概率密度函数所绘制的分布曲线
概率分布函数:
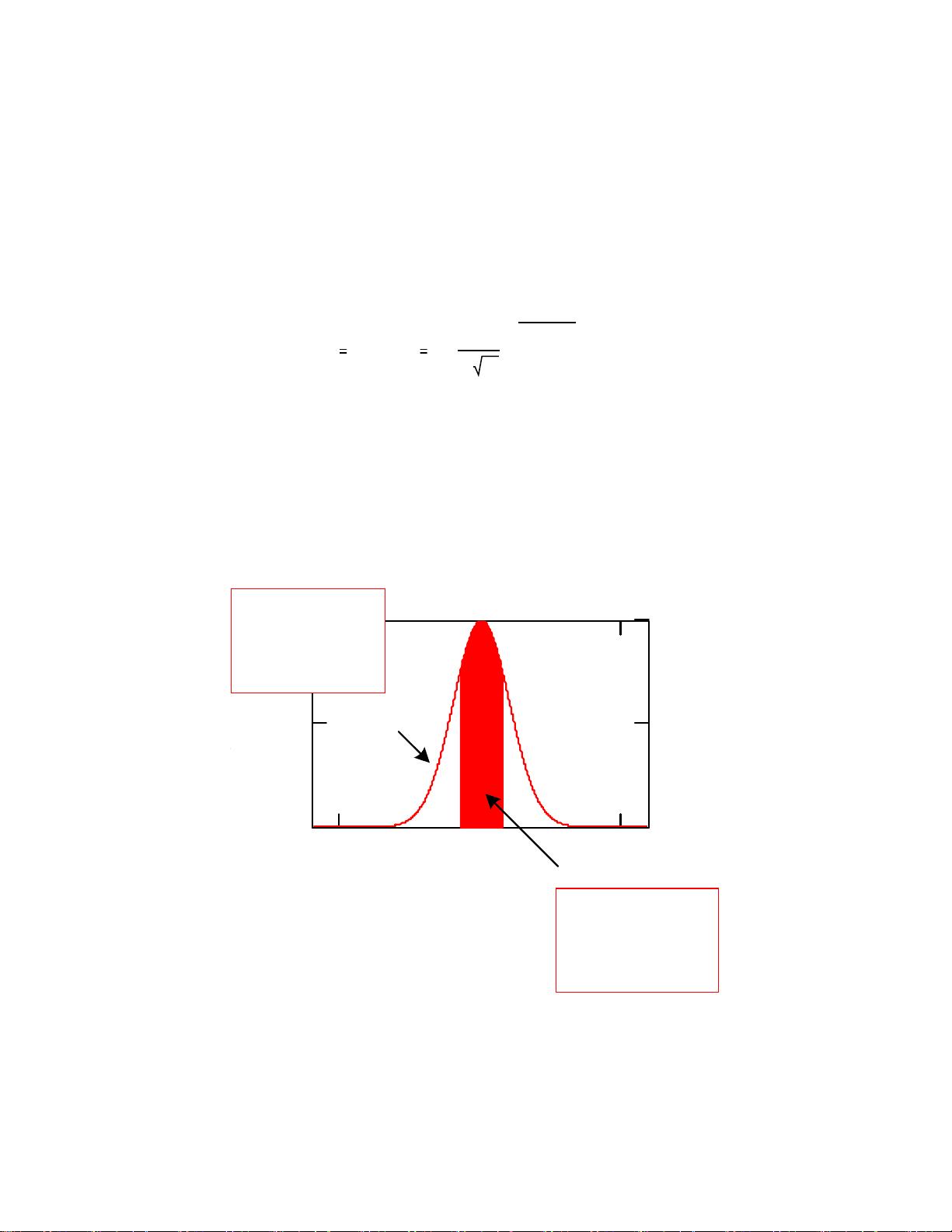
概率分布函数是概率密度函数的积分。根据该函数,我们可了解某事件在给定的时
间间隔内发生的概率(见方程式 1.3 与图 1.3)。举例来说,我们可以假定图 1.4 为
噪声概率分布函数,该函数告诉我们,在任意时间点上,在 1V 与 +1V 之间(即 (-
1, 1) 区间内)检测到噪声电压的概率为 30%。
Pa x< b<()
a
b
xfx()
⌠
⎮
⌡
d
a
b
x
1
σ 2π
⋅
e
x µ−()
2
−
2σ
2
⎡
⎢
⎢
⎣
⎤
⎥
⎥
⎦
⋅
⌠
⎮
⎮
⎮
⎮
⌡
d
Where
P(a < x < b) -- the probability that x will be in the interval (a, b)
x-- the random variable. In this case noise voltage.
µ
-- the mean value
σ
-- the standard deviation
方程式 1.3: 概率分布函数
50 5
0
0.2
0.4
x)
x
ab
f(x)
P(a<x<b)
Probability
Density
Function
Probability
Distribution
Function
图 1.3: 概率密度函数与概率分布函数
概率分布函数对我们将 RMS 热噪声电压转化为峰值对峰值噪声非常有用。请注
意,高斯分布曲线的尾部是无限延伸的,这就是说,任何噪声电压都是可能的。尽
管理论上确实如此,但就实际情况而言,极大的瞬时噪声电压发生的可能性不大。
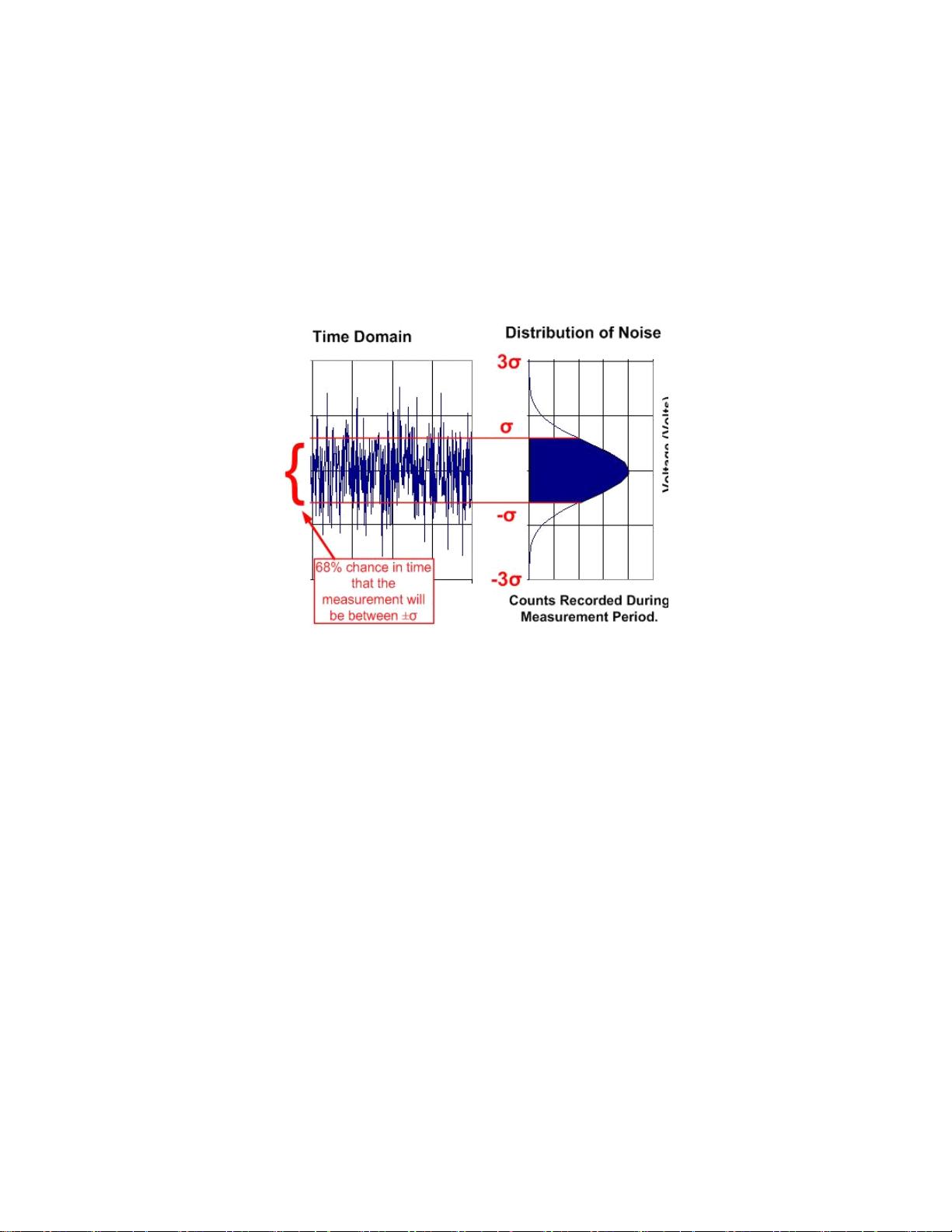
举例来说,我们检测到噪声电压在 -3σ 与 +3σ 之间的概率为 99.7 %。换言之,噪
声电压超出该范围的概率仅有 0.3 %。因此,我们通常将噪声信号的峰值估算为
±3σ(即 6σ)。请注意,也有些工程师将噪声的峰值估算为 6.6σ。人们对到底如何
估计这个数值没有定论。图 1.4 显示,68% 的噪声都会不超过 2σ。表 1.1 总结了测
量噪声电压时标准偏差与概率之间的关系。
图 1.4: 标准偏差与峰值噪声间的关系
剩余156页未读,继续阅读
资源评论

lukunn
- 粉丝: 0
- 资源: 9
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 基于微信小程序校园外卖系统-数据库课程设计全部资料+详细文档+高分项目.zip
- 基于图书馆系统,swing界面,基本数据库操作全部资料+详细文档+高分项目.zip
- 基于图书管理系统(数据库课程设计,原生PHP+Bootstrap+MySQL)全部资料+详细文档+高分项目.zip
- 基于学生信息管理系统 JAVA Mysql 数据库课程设计 简单界面全部资料+详细文档+高分项目.zip
- 基于学生教务信息管理系统:SQL SERVER数据库课程设计全部资料+详细文档+高分项目.zip
- 2024中国数字化年会演讲(脱敏)PPT汇总(9份).zip
- Java+Swing+Mysql实现图书管理系统.zip
- 充电桩通讯协议 CAN标准帧
- 2024年数据治理产业图谱3.0(高清大图).pdf
- Java+Swing+Mysql实现学生信息管理系统.zip
- 吊篮式油菜移栽机sw16可编辑全套技术资料100%好用.zip
- C3传奇3引擎+版本全套 免费分享
- 123swwdqdsqwdqd
- 钢筋滚丝机sw18可编辑全套技术资料100%好用.zip
- 滚筒线体及托盘下料设备sw17全套技术资料100%好用.zip
- 基于java+ssm+mysql的鲜花商城系统开题报告.doc
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功