Efficient Algorithms and Intractable Problems_ch5

preview
试读
29页
Efficient
Algorithms
Intractable
Problems
需积分: 0 0 下载量 126 浏览量 更新于2010-03-17 收藏 285KB PDF 举报
### 高效算法与难解问题：贪婪算法与最小生成树 #### 贪婪算法概览 在探讨高效算法与难解问题时，我们不可避免地会遇到贪婪算法这一类特殊的算法策略。这类算法通常通过一系列简单且直观的决策来构建解决方案。尽管这种短视的行为在某些计算任务中可能会导致灾难性的后果，但在很多情况下它却是最优的选择之一。 #### 贪婪算法的特点 贪婪算法的基本思想是在每个步骤中选择局部最优解，希望通过这种方式能够达到全局最优解。这种方法的优点在于其简单易实现，并且在某些特定的问题上能够获得非常好的效果。然而，它也存在明显的局限性——即当整体最优解不能通过一系列局部最优解来实现时，贪婪算法就可能无法达到最优解。 #### 最小生成树 一个经典的贪婪算法应用场景是求解最小生成树问题。假设我们需要连接一组计算机，使得它们之间可以通过特定的链接相互通信，同时希望这些链接的成本尽可能低。这可以抽象为一个图论问题，其中节点代表计算机，无向边表示潜在的链接，并且每条边都有一个与其成本相关的权重。 目标是最小化所有边的总权重，从而形成一个连接所有节点的树形结构。这样的树被称为**最小生成树**（Minimum Spanning Tree, MST）。 #### 最小生成树的形式定义 输入为一个无向图 \( G = (V, E) \)，其中 \( V \) 表示顶点集，\( E \) 表示边集；每条边有一个与之关联的权重 \( w_e \)。 输出为一棵树 \( T = (V, E') \)，其中 \( E' \subseteq E \)，且满足 \[ \text{weight}(T) = \sum_{e \in E'} w_e \] 是所有可能的树中最小的。 #### 性质分析 一个重要的观察是，最优解中的边集不能包含任何环路。这是因为，如果存在环路，则移除环路中的任意一条边都不会破坏连通性，但可以降低总成本。因此，最小生成树必然是一个没有环路的连通子图，即一棵树。 #### 构建最小生成树的贪婪方法 克鲁斯卡尔算法（Kruskal's Algorithm）是一种构建最小生成树的经典贪婪算法。该算法从一个空图开始，然后按照以下规则逐步添加边： 1. **初始化**：创建一个空集合用来存储最终的最小生成树的边集。 2. **排序**：将所有的边按照权重从小到大进行排序。 3. **遍历**：依次考虑每条边，对于当前考虑的边： - 如果这条边的两个端点不在同一个连通分量中，则将这条边加入到最小生成树的边集中。 - 否则，跳过这条边。 4. **结束**：当所有边都被考虑过后，得到的边集构成了一棵最小生成树。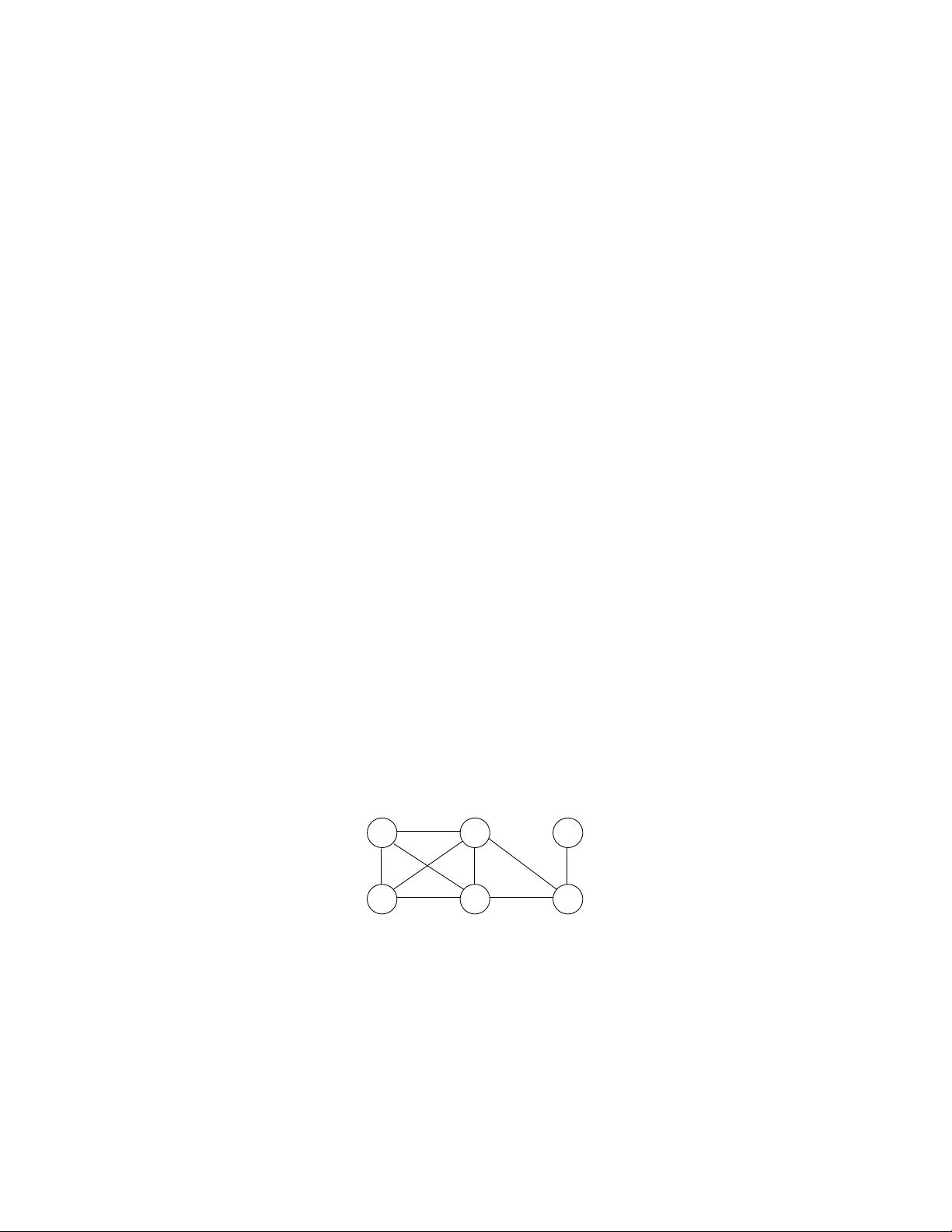 #### 克鲁斯卡尔算法的执行过程 以图示中的例子为例： - 图中的顶点为 A、B、C、D、E 和 F。 - 边及其权重分别为：(A, B) 1, (B, C) 2, (C, D) 4, (D, E) 4, (E, F) 5, (A, C) 4, (A, D) 4, (B, D) 3, (B, F) 6, (C, F) 4。 - 按照权重排序后依次考虑每条边。 最终形成的最小生成树如图所示，其总权重为 16。需要注意的是，这并不是唯一可能的最小生成树。例如，通过不同的选择顺序，也可以得到相同权重的其他最小生成树。 #### 结论 通过上述讨论可以看出，贪婪算法在解决最小生成树问题时是非常有效的。它不仅简单易于理解，而且在很多情况下都能够给出最优解。然而，在应用贪婪算法时也需要谨慎，因为它并不能保证在所有问题上都能找到全局最优解。
Chapter 5
Greedy algorithms
A game like chess can be won only by thinking ahead: a player who is focused entirely on
immediate advantage is easy to defeat. But in many other games, such as Scrabble, it is
possible to do quite well by simply making whichever move seems best at the moment and not
worrying too much about future consequences.
This sort of myopic behavior is easy and convenient, making it an attractive algorithmic
strategy. Greedy algorithms build up a solution piece by piece, always choosing the next
piece that offers the most obvious and immediate benefit. Although such an approach can be
disastrous for some computational tasks, there are many for which it is optimal. Our first
example is that of minimum spanning trees.
5.1 Minimum spanning trees
Suppose you are asked to network a collection of computers by linking selected pairs of them.
This translates into a graph problem in which nodes are computers, undirected edges are
potential links, and the goal is to pick enough of these edges that the nodes are connected.
But this is not all; each link also has a maintenance cost, reflected in that edge’s weight. What
is the cheapest possible network?
A
B
C
D
E
F
4
1
4
3
4
2
5
6
4
One immediate observation is that the optimal set of edges cannot contain a cycle, because
removing an edge from this cycle would reduce the cost without compromising connectivity:
Property 1
Removing a cycle edge cannot disconnect a graph.
So the solution must be connected and acyclic: undirected graphs of this kind are called
trees. The particular tree we want is the one with minimum total weight, known as the
minimum spanning tree. Here is its formal definition.
139
140
Algorithms
Input: An undirected graph G = (V, E); edge weights w
e
.
Output: A tree T = (V, E
0
), with E
0
⊆ E, that minimizes
weight(T ) =
X
e∈E
0
w
e
.
In the preceding example, the minimum spanning tree has a cost of 16:
A
B
C
D
E
F
1
4
2
5
4
However, this is not the only optimal solution. Can you spot another?
5.1.1 A greedy approach
Kruskal’s minimum spanning tree algorithm starts with the empty graph and then selects
edges from E according to the following rule.
Repeatedly add the next lightest edge that doesn’t produce a cycle.
In other words, it constructs the tree edge by edge and, apart from taking care to avoid cycles,
simply picks whichever edge is cheapest at the moment. This is a greedy algorithm: every
decision it makes is the one with the most obvious immediate advantage.
Figure 5.1 shows an example. We start with an empty graph and then attempt to add
edges in increasing order of weight (ties are broken arbitrarily):
B − C, C − D, B − D, C − F, D − F, E − F, A − D, A − B, C − E, A − C.
The first two succeed, but the third, B − D, would produce a cycle if added. So we ignore it
and move along. The final result is a tree with cost 14, the minimum possible.
The correctness of Kruskal’s method follows from a certain cut property, which is general
enough to also justify a whole slew of other minimum spanning tree algorithms.
Figure 5.1 The minimum spanning tree found by Kruskal’s algorithm.
B
A
6
5
3
4
2
F
D
C
E
5
4
1
2
4
B
A
F
D
C
E
S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani
141
Trees
A tree is an undirected graph that is connected and acyclic. Much of what makes trees so
useful is the simplicity of their structure. For instance,
Property 2
A tree on
n
nodes has
n − 1
edges.
This can be seen by building the tree one edge at a time, starting from an empty graph.
Initially each of the n nodes is disconnected from the others, in a connected component by
itself. As edges are added, these components merge. Since each edge unites two different
components, exactly n − 1 edges are added by the time the tree is fully formed.
In a little more detail: When a particular edge {u, v} comes up, we can be sure that u
and v lie in separate connected components, for otherwise there would already be a path
between them and this edge would create a cycle. Adding the edge then merges these two
components, thereby reducing the total number of connected components by one. Over the
course of this incremental process, the number of components decreases from n to one,
meaning that n − 1 edges must have been added along the way.
The converse is also true.
Property 3
Any connected, undirected graph
G = (V, E)
with
|E| = |V | − 1
is a tree.
We just need to show that G is acyclic. One way to do this is to run the following iterative
procedure on it: while the graph contains a cycle, remove one edge from this cycle. The
process terminates with some graph G
0
= (V, E
0
), E
0
⊆ E, which is acyclic and, by Property 1
(from page 139), is also connected. Therefore G
0
is a tree, whereupon |E
0
| = |V | − 1 by
Property 2. So E
0
= E, no edges were removed, and G was acyclic to start with.
In other words, we can tell whether a connected graph is a tree just by counting how
many edges it has. Here’s another characterization.
Property 4
An undirected graph is a tree if and only if there is a unique path between any
pair of nodes.
In a tree, any two nodes can only have one path between them; for if there were two
paths, the union of these paths would contain a cycle.
On the other hand, if a graph has a path between any two nodes, then it is connected. If
these paths are unique, then the graph is also acyclic (since a cycle has two paths between
any pair of nodes).
142
Algorithms
Figure 5.2 T ∪ {e}. The addition of e (dotted) to T (solid lines) produces a cycle. This cycle
must contain at least one other edge, shown here as e
0
, across the cut (S, V − S).
e
S
V − S
e
0
5.1.2 The cut property
Say that in the process of building a minimum spanning tree (MST), we have already chosen
some edges and are so far on the right track. Which edge should we add next? The following
lemma gives us a lot of flexibility in our choice.
Cut property
Suppose edges
X
are part of a minimum spanning tree of
G = (V, E)
. Pick any
subset of nodes
S
for which
X
does not cross between
S
and
V − S
, and let
e
be the lightest
edge across this partition. Then
X ∪ {e}
is part of some MST.
A cut is any partition of the vertices into two groups, S and V − S. What this property says
is that it is always safe to add the lightest edge across any cut (that is, between a vertex in S
and one in V − S), provided X has no edges across the cut.
Let’s see why this holds. Edges X are part of some MST T ; if the new edge e also happens
to be part of T , then there is nothing to prove. So assume e is not in T . We will construct a
different MST T
0
containing X ∪ {e} by altering T slightly, changing just one of its edges.
Add edge e to T . Since T is connected, it already has a path between the endpoints of e, so
adding e creates a cycle. This cycle must also have some other edge e
0
across the cut (S, V − S)
(Figure 8.3). If we now remove this edge, we are left with T
0
= T ∪ {e} − {e
0
}, which we will
show to be a tree. T
0
is connected by Property 1, since e
0
is a cycle edge. And it has the same
number of edges as T ; so by Properties 2 and 3, it is also a tree.
Moreover, T
0
is a minimum spanning tree. Compare its weight to that of T :
weight(T
0
) = weight(T ) + w(e) − w(e
0
).
Both e and e
0
cross between S and V − S, and e is specifically the lightest edge of this type.
Therefore w(e) ≤ w(e
0
), and weight(T
0
) ≤ weight(T ). Since T is an MST, it must be the case
that weight(T
0
) = weight(T ) and that T
0
is also an MST.
Figure 5.3 shows an example of the cut property. Which edge is e
0
?
S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani
143
Figure 5.3 The cut property at work. (a) An undirected graph. (b) Set X has three edges, and
is part of the MST T on the right. (c) If S = {A, B, C, D}, then one of the minimum-weight
edges across the cut (S, V − S) is e = {D, E}. X ∪ {e} is part of MST T
0
, shown on the right.
(a)
A
B
C
E
F
D
2
2
3
3
41
1
2
1
(b)
Edges X:
A
B
C
E
F
D
MST T :
A
B
C
E
F
D
(c)
The cut:
A
B
C
E
F
D
e
S
V − S
MST T
0
:
A
B
C
E
F
D
5.1.3 Kruskal’s algorithm
We are ready to justify Kruskal’s algorithm. At any given moment, the edges it has already
chosen form a partial solution, a collection of connected components each of which has a tree
structure. The next edge e to be added connects two of these components; call them T
1
and
T
2
. Since e is the lightest edge that doesn’t produce a cycle, it is certain to be the lightest edge
between T
1
and V − T
1
and therefore satisfies the cut property.
Now we fill in some implementation details. At each stage, the algorithm chooses an edge
to add to its current partial solution. To do so, it needs to test each candidate edge u − v to
see whether the endpoints u and v lie in different components; otherwise the edge produces a
cycle. And once an edge is chosen, the corresponding components need to be merged. What
kind of data structure supports such operations?
We will model the algorithm’s state as a collection of disjoint sets, each of which contains
the nodes of a particular component. Initially each node is in a component by itself:
makeset(x): create a singleton set containing just x.
We repeatedly test pairs of nodes to see if they belong to the same set.
find(x): to which set does x belong?

剩余28页未读，继续阅读

资源推荐
资源评论
luckyfancy
  • 粉丝: 0
  • 资源: 15
上传资源 快速赚钱
voice
center-task 前往需求广场，查看用户热搜

最新资源