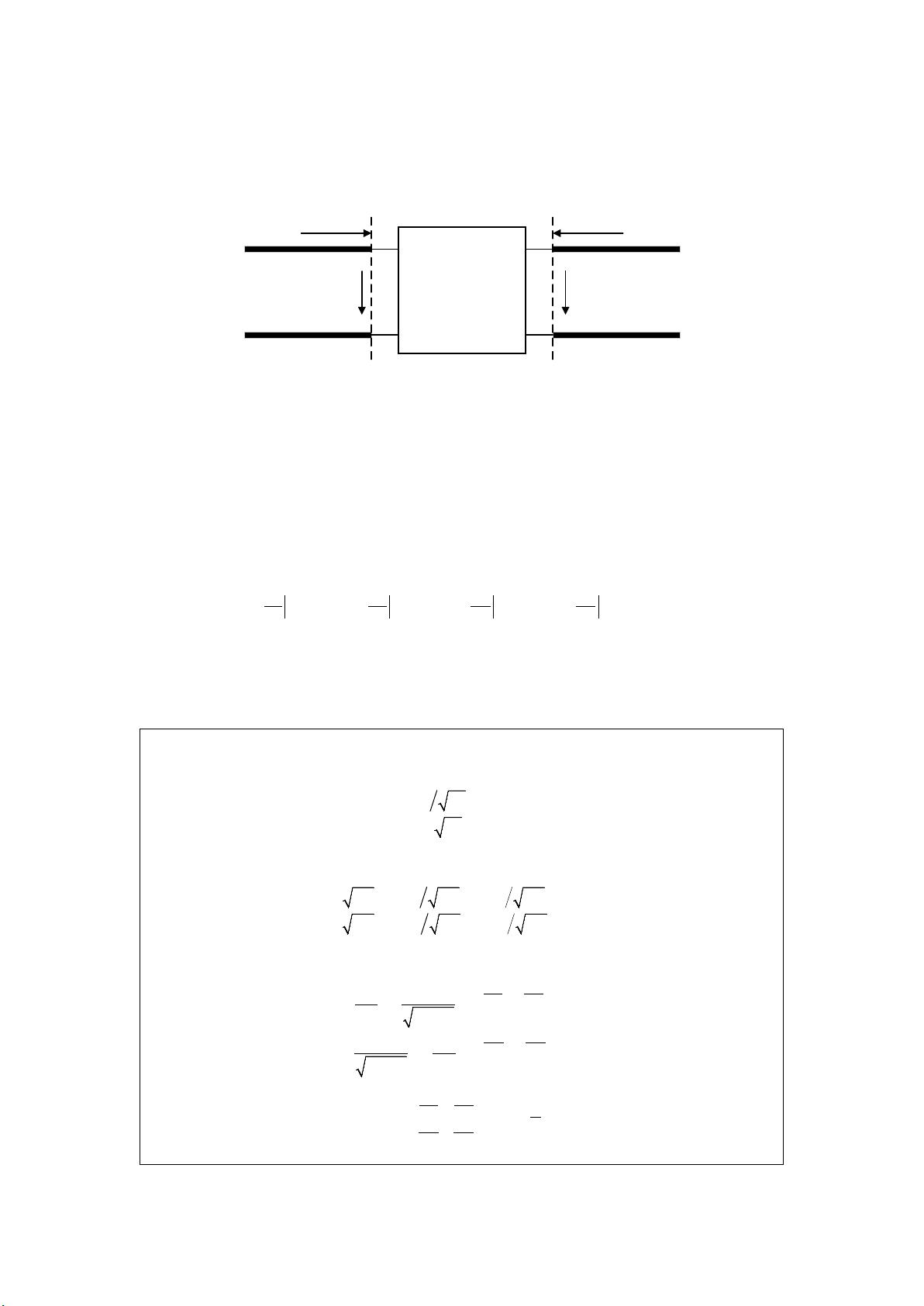
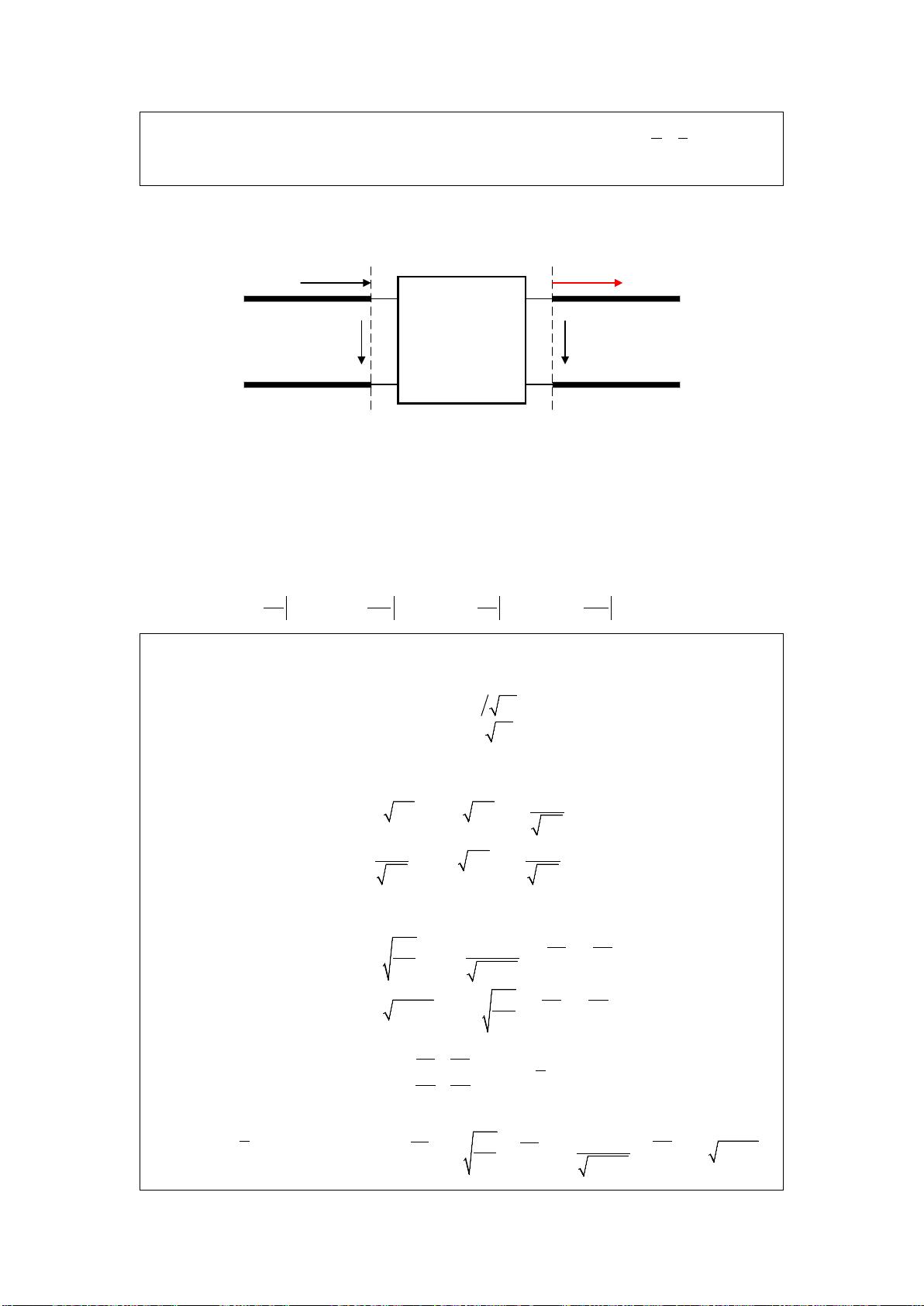
### 微波网络中的参数矩阵定义、推导及其转换
#### 一、Z矩阵（阻抗矩阵）
在微波工程领域，二端口网络是非常重要的组成部分。为了方便分析和计算，引入了不同的参数矩阵来描述这些网络的行为。首先介绍的是**Z矩阵**。
**定义：**
Z矩阵用于描述端口电压与端口电流之间的关系。对于一个二端口网络，假设其两个端口的电压分别为\(U_1\)和\(U_2\)，对应的电流分别为\(I_1\)和\(I_2\)，则可以定义Z矩阵如下：
\[
\begin{align*}
U_1 &= Z_{11}I_1 + Z_{12}I_2 \\
U_2 &= Z_{21}I_1 + Z_{22}I_2
\end{align*}
\]
或者用矩阵形式表示为：
\[
\begin{bmatrix}
U_1 \\
U_2
\end{bmatrix}
=
\begin{bmatrix}
Z_{11} & Z_{12} \\
Z_{21} & Z_{22}
\end{bmatrix}
\begin{bmatrix}
I_1 \\
I_2
\end{bmatrix}
\]
**特殊性质：**
- **对于互易网络**：\(Z_{12} = Z_{21}\)
- **对于对称网络**：\(Z_{11} = Z_{22}\)
- **对于无耗网络**：每个元素都可以表示为纯虚数，即\(Z_{ij} = jX_{ij}\)，其中\(X_{ij}\)为实数。
**归一化阻抗矩阵**：
为了进一步简化计算，通常会定义归一化的电压和电流，以及相应的归一化阻抗矩阵。设归一化电压和电流为\(u\)和\(i\)，则它们与未归一化的电压和电流之间的关系为：
\[
\begin{align*}
u &= \frac{U}{Z_0} \\
i &= \frac{I}{Z_0}
\end{align*}
\]
其中\(Z_0\)为参考阻抗。由此，我们可以得到归一化的Z矩阵为：
\[
\begin{bmatrix}
u_1 \\
u_2
\end{bmatrix}
=
\begin{bmatrix}
z_{11} & z_{12} \\
z_{21} & z_{22}
\end{bmatrix}
\begin{bmatrix}
i_1 \\
i_2
\end{bmatrix}
\]
这里的\(z_{ij}\)是归一化后的阻抗矩阵元素。
#### 二、Y矩阵（导纳矩阵）
**定义：**
Y矩阵是用来描述端口电流与端口电压之间的关系的。对于二端口网络，Y矩阵定义为：
\[
\begin{align*}
I_1 &= Y_{11}U_1 + Y_{12}U_2 \\
I_2 &= Y_{21}U_1 + Y_{22}U_2
\end{align*}
\]
或用矩阵形式表示为：
\[
\begin{bmatrix}
I_1 \\
I_2
\end{bmatrix}
=
\begin{bmatrix}
Y_{11} & Y_{12} \\
Y_{21} & Y_{22}
\end{bmatrix}
\begin{bmatrix}
U_1 \\
U_2
\end{bmatrix}
\]
**特殊性质：**
- **对于互易网络**：\(Y_{12} = Y_{21}\)
- **对于对称网络**：\(Y_{11} = Y_{22}\)
- **对于无耗网络**：每个元素都是纯虚数，即\(Y_{ij} = jB_{ij}\)，其中\(B_{ij}\)为实数。
**归一化导纳矩阵**：
同样地，可以定义归一化的电压和电流，并据此定义归一化的导纳矩阵。设归一化电压和电流为\(u\)和\(i\)，则有：
\[
\begin{align*}
u &= \frac{U}{Z_0} \\
i &= \frac{I}{Z_0}
\end{align*}
\]
归一化的Y矩阵为：
\[
\begin{bmatrix}
i_1 \\
i_2
\end{bmatrix}
=
\begin{bmatrix}
y_{11} & y_{12} \\
y_{21} & y_{22}
\end{bmatrix}
\begin{bmatrix}
u_1 \\
u_2
\end{bmatrix}
\]
这里的\(y_{ij}\)是归一化后的导纳矩阵元素。
#### 三、A矩阵（散射参数矩阵）
A矩阵主要用于描述网络内部的信号传输情况，尤其是信号在不同端口间的传输关系。它通过定义网络输入和输出端口的电压电流比来描述网络特性。A矩阵的定义如下：
\[
\begin{align*}
\begin{bmatrix}
U_1' \\
I_1'
\end{bmatrix}
&=
\begin{bmatrix}
A_{11} & A_{12} \\
A_{21} & A_{22}
\end{bmatrix}
\begin{bmatrix}
U_2 \\
-I_2
\end{bmatrix}
\end{align*}
\]
其中\(U_1'\)和\(I_1'\)分别表示网络输入端口的电压和电流，\(U_2\)和\(-I_2\)分别表示网络输出端口的电压和负电流。
**特殊性质：**
- **对于互易网络**：\(A_{12} = -A_{21}\)
#### 四、S矩阵（散射矩阵）
S矩阵是微波工程中最常用的参数之一，用来描述二端口网络的散射特性。它定义了网络输入端口和输出端口之间反射和透射的比率。S矩阵的定义如下：
\[
\begin{align*}
\begin{bmatrix}
b_1 \\
b_2
\end{bmatrix}
&=
\begin{bmatrix}
S_{11} & S_{12} \\
S_{21} & S_{22}
\end{bmatrix}
\begin{bmatrix}
a_1 \\
a_2
\end{bmatrix}
\end{align*}
\]
其中\(a_i\)和\(b_i\)分别表示入射波和反射波的幅度。
**特殊性质：**
- **对于互易网络**：\(S_{12} = S_{21}\)
#### 五、T矩阵（传输参数矩阵）
T矩阵，也称为传输参数矩阵，用于描述信号在二端口网络内部的传输特性。它可以直观地表示信号从一个端口到另一个端口的传输情况。T矩阵定义如下：
\[
\begin{align*}
\begin{bmatrix}
U_2 \\
I_2
\end{bmatrix}
&=
\begin{bmatrix}
T_{11} & T_{12} \\
T_{21} & T_{22}
\end{bmatrix}
\begin{bmatrix}
U_1 \\
I_1
\end{bmatrix}
\end{align*}
\]
**特殊性质：**
- **对于互易网络**：\(T_{11}T_{22} - T_{12}T_{21} = 1\)
### 参数矩阵之间的转换
不同参数矩阵之间可以通过特定的数学变换进行转换，以便于根据实际应用场景选择最适合的参数矩阵进行分析和设计。以下是一些基本的转换公式：
- **Z到Y**：
\[
\begin{bmatrix}
Y_{11} & Y_{12} \\
Y_{21} & Y_{22}
\end{bmatrix}
=
\begin{bmatrix}
Z_{11} & Z_{12} \\
Z_{21} & Z_{22}
\end{bmatrix}^{-1}
\]
- **Y到Z**：
\[
\begin{bmatrix}
Z_{11} & Z_{12} \\
Z_{21} & Z_{22}
\end{bmatrix}
=
\begin{bmatrix}
Y_{11} & Y_{12} \\
Y_{21} & Y_{22}
\end{bmatrix}^{-1}
\]
- **Z到S**：
\[
\begin{bmatrix}
S_{11} & S_{12} \\
S_{21} & S_{22}
\end{bmatrix}
=
\begin{bmatrix}
\frac{Z_{11}-Z_0}{Z_{11}+Z_0} & \frac{2Z_{12}}{Z_{11}+Z_{22}+Z_0} \\
\frac{2Z_{21}}{Z_{11}+Z_{22}+Z_0} & \frac{Z_{22}-Z_0}{Z_{22}+Z_0}
\end{bmatrix}
\]
- **S到Z**：
\[
\begin{bmatrix}
Z_{11} & Z_{12} \\
Z_{21} & Z_{22}
\end{bmatrix}
=
Z_0
\begin{bmatrix}
\frac{1+S_{11}}{1-S_{11}} & \frac{2S_{12}}{1-S_{11}S_{22}} \\
\frac{2S_{21}}{1-S_{11}S_{22}} & \frac{1+S_{22}}{1-S_{22}}
\end{bmatrix}
\]
通过上述定义和转换，可以灵活地在不同参数矩阵间进行切换，从而更好地理解微波网络的工作原理，并为其设计提供理论支持。
