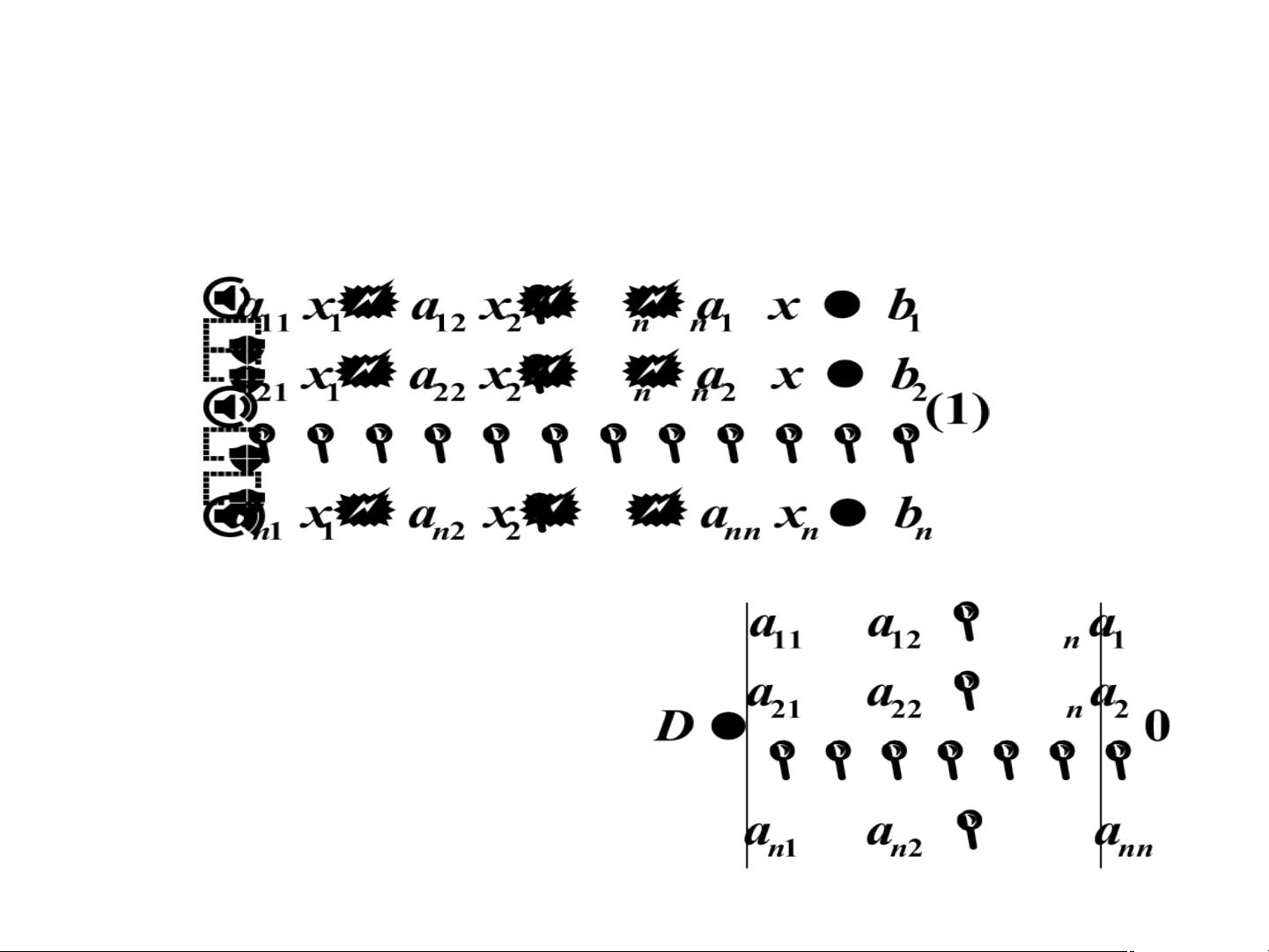
克拉默法则是一种求解线性方程组的方法,尤其适用于二元或多元线性方程组。当线性方程组的系数行列式不为零时,克拉默法则提供了求解方程组的一种直接途径。在描述中提到的定理表明,如果线性方程组的系数行列式\( D \neq 0 \),那么该方程组不仅有解,而且解是唯一的。
克拉默法则的具体表述如下:给定一个二元线性方程组:
\[ ax + by = e \]
\[ cx + dy = f \]
其中\( a, b, c, d, e, f \)是常数,\( x \)和\( y \)是未知数。系数行列式\( D \)定义为:
\[ D = \begin{vmatrix}
a & b \\
c & d \\
\end{vmatrix} = ad - bc \]
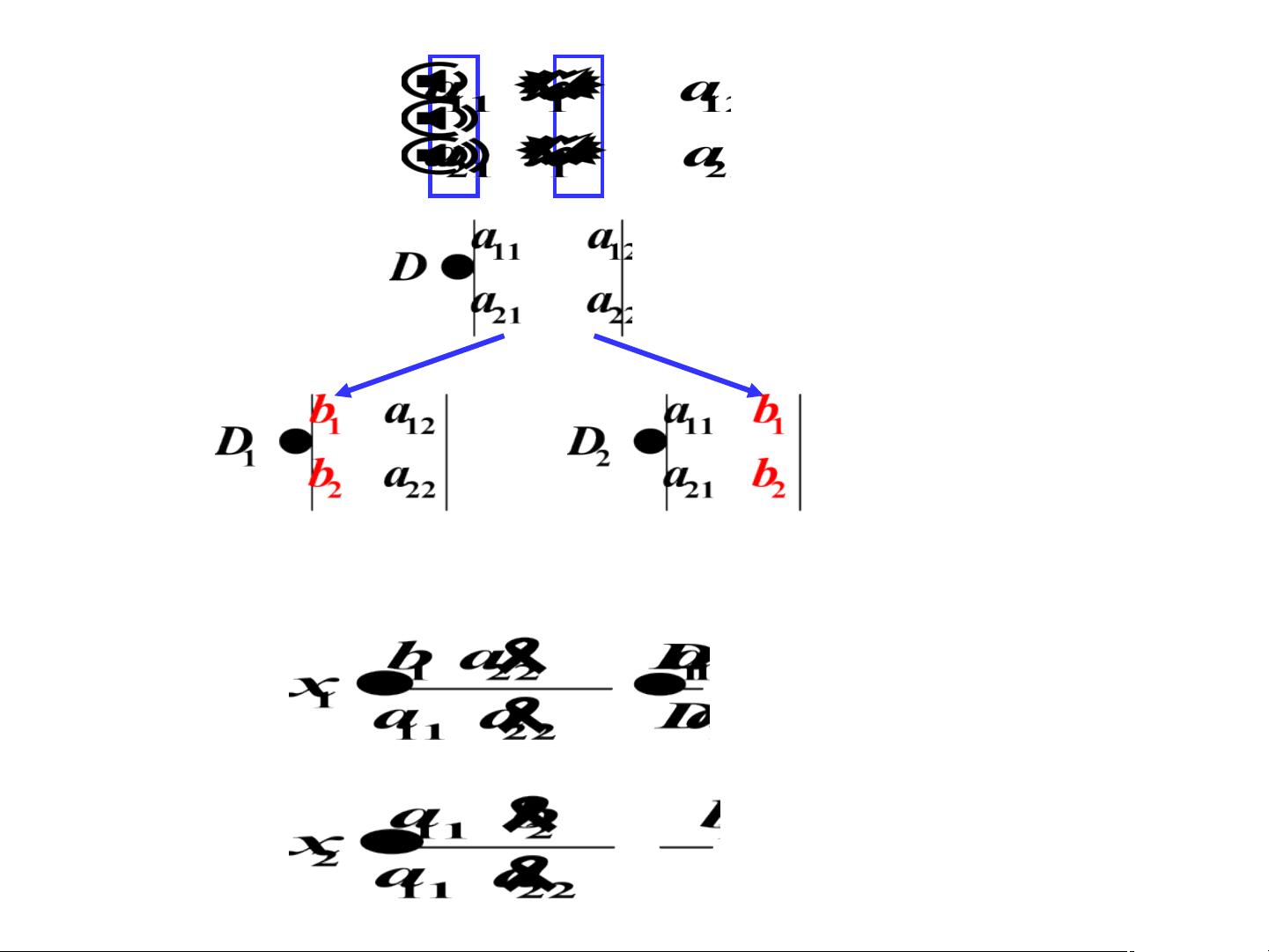
如果\( D \neq 0 \),那么可以构造两个新的行列式\( D_x \)和\( D_y \),它们分别是将原行列式的第\( i \)列替换为常数项后的结果,例如对于\( x \)的解,我们有:
\[ D_x = \begin{vmatrix}
e & b \\
f & d \\
\end{vmatrix} \]
同样,对于\( y \)的解,我们有:
\[ D_y = \begin{vmatrix}
a & e \\
c & f \\
\end{vmatrix} \]
根据克拉默法则,线性方程组的解\( x \)和\( y \)可以通过以下方式计算:
\[ x = \frac{D_x}{D}, \quad y = \frac{D_y}{D} \]
需要注意的是,克拉默法则并不适用于系数行列式为零的情况。当\( D = 0 \)时,方程组可能无解,也可能有无穷多个解。对于齐次线性方程组(所有常数项为零的方程组),如果系数行列式\( D \neq 0 \),则方程组仅有零解。相反,如果\( D = 0 \),齐次线性方程组可能有非零解。
总结一下,克拉默法则的核心要点:
1. 方程组的系数行列式不为零是应用克拉默法则的必要条件。
2. 当满足此条件时,方程组的解是唯一且可以通过行列式的代换直接计算。
3. 对于齐次线性方程组,系数行列式不为零意味着只有零解,而为零则可能存在非零解。
4. 当系数行列式为零时,不能使用克拉默法则,因为此时方程组可能无解或有无穷多解。
在解决实际问题时,克拉默法则提供了一种直接的计算方法,但其适用范围有限,不适用于系数行列式为零的情况,或在方程个数与未知数数量不相等的方程组中。在这些情况下,通常需要其他方法,如高斯消元法或矩阵求逆来解决。