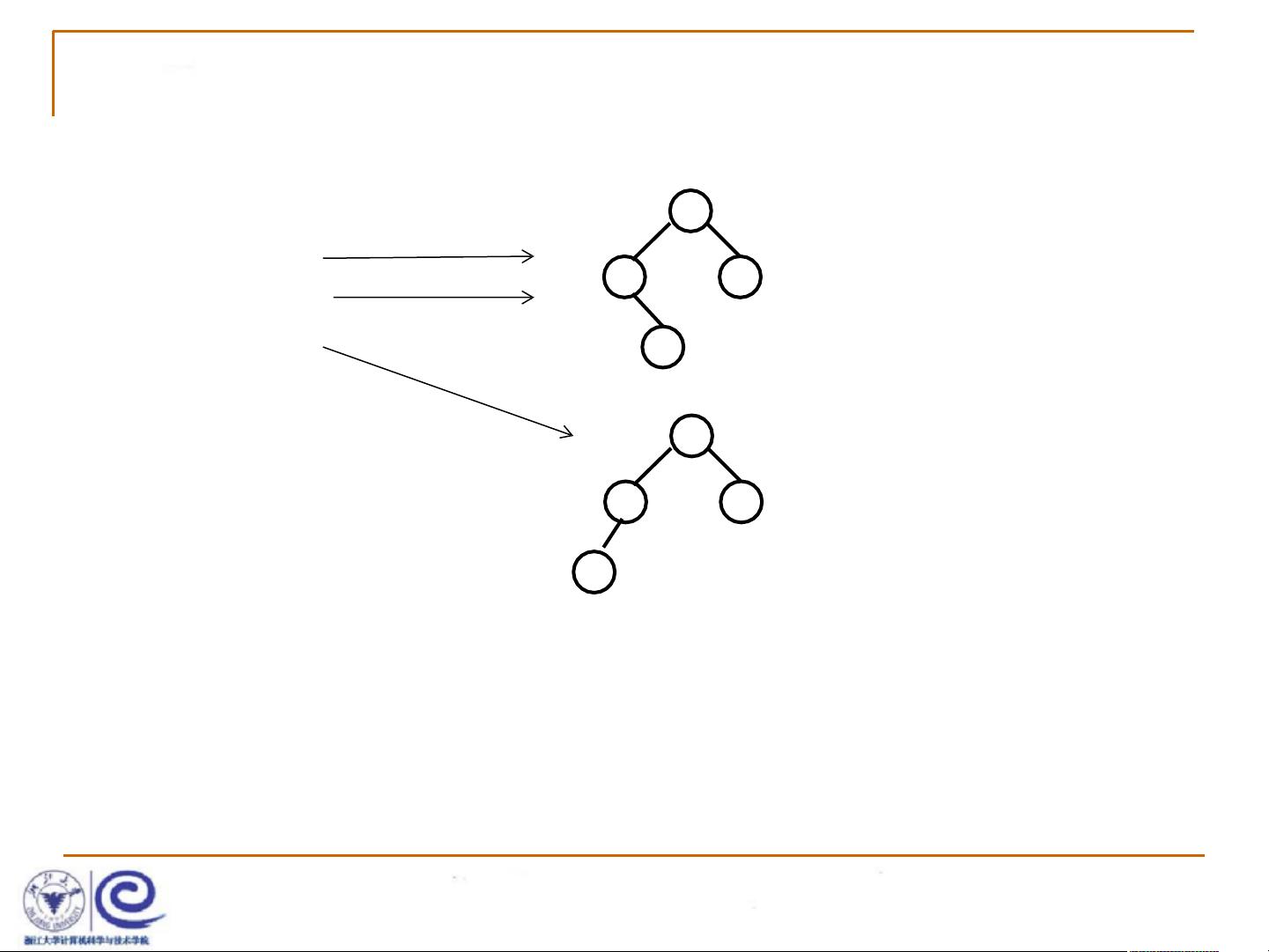
判断同一棵二叉搜索树
本资源旨在解决判断同一棵二叉搜索树问题,即给定多个插入序列,判断它们是否能生成一样的二叉搜索树。
知识点:
1. 二叉搜索树(Binary Search Tree,BST):是一种特殊的二叉树,每个节点的值大于或等于左子树中的所有节点值,小于或等于右子树中的所有节点值。
2. 插入序列:是指将一系列数字插入到一个空的二叉搜索树中,生成一个二叉搜索树。
3. 判断同一棵二叉搜索树:是指给定多个插入序列,判断它们是否能生成一样的二叉搜索树。
4. 解决思路:
1. 分别建两棵搜索树的判别方法:分别根据两个序列生成两棵二叉搜索树,然后判断这两棵树是否一样。
2. 不建树的判别方法:不生成二叉搜索树,而是直接判断两个序列是否能生成一样的二叉搜索树。
3. 建一棵树,再判别其他序列是否与该树一致:生成一棵二叉搜索树,然后判断其他序列是否能生成一样的二叉搜索树。
5. 程序框架:
```c
int main(){
int N, L, i;
Tree T;
scanf("%d", &N);
while (N) {
scanf("%d", &L);
T = MakeTree(N);
for (i=0; i<L; i++) {
if (Judge(T, N))
printf("Yes\n");
else
printf("No\n");
ResetT(T);
}
FreeTree(T);
scanf("%d", &N);
}
return 0;
}
```
6. 主要函数:
1. 读数据建搜索树T:MakeTree函数用于读取输入数据,生成一棵二叉搜索树。
2. 判别一序列是否与T构成一样的搜索树:Judge函数用于判断一个序列是否能生成一样的二叉搜索树。
7. 如何建搜索树:
```c
Tree MakeTree( int N ){
Tree T;
int i, V;
scanf("%d", &V);
T = NewNode(V);
for (i=1; i<N; i++) {
scanf("%d", &V);
T = Insert(T, V);
}
return T;
}
```
8. 如何判别:
```c
int check ( Tree T, int V ){
if ( T->flag ) {
if ( V<T->v )
return check(T->Left, V);
else if ( V>T->v )
return check(T->Right, V);
else
return 0;
}else {
if ( V==T->v ) {
T->flag = 1;
return 1;
}else
return 0;
}
}
```
9. 判别函数:
```c
int Judge( Tree T, int N ){
int i, V, flag = 0;
scanf("%d", &V);
if ( V!=T->v )
return 0;
else
T->flag = 1;
for (i=1; i<N; i++) {
scanf("%d", &V);
if (!check(T, V) )
return 0;
}
return 1;
}
```
本资源旨在解决判断同一棵二叉搜索树问题,通过分析问题的需求,设计了解决思路和主要函数,提供了详细的代码实现。