蒙特卡洛算法入门

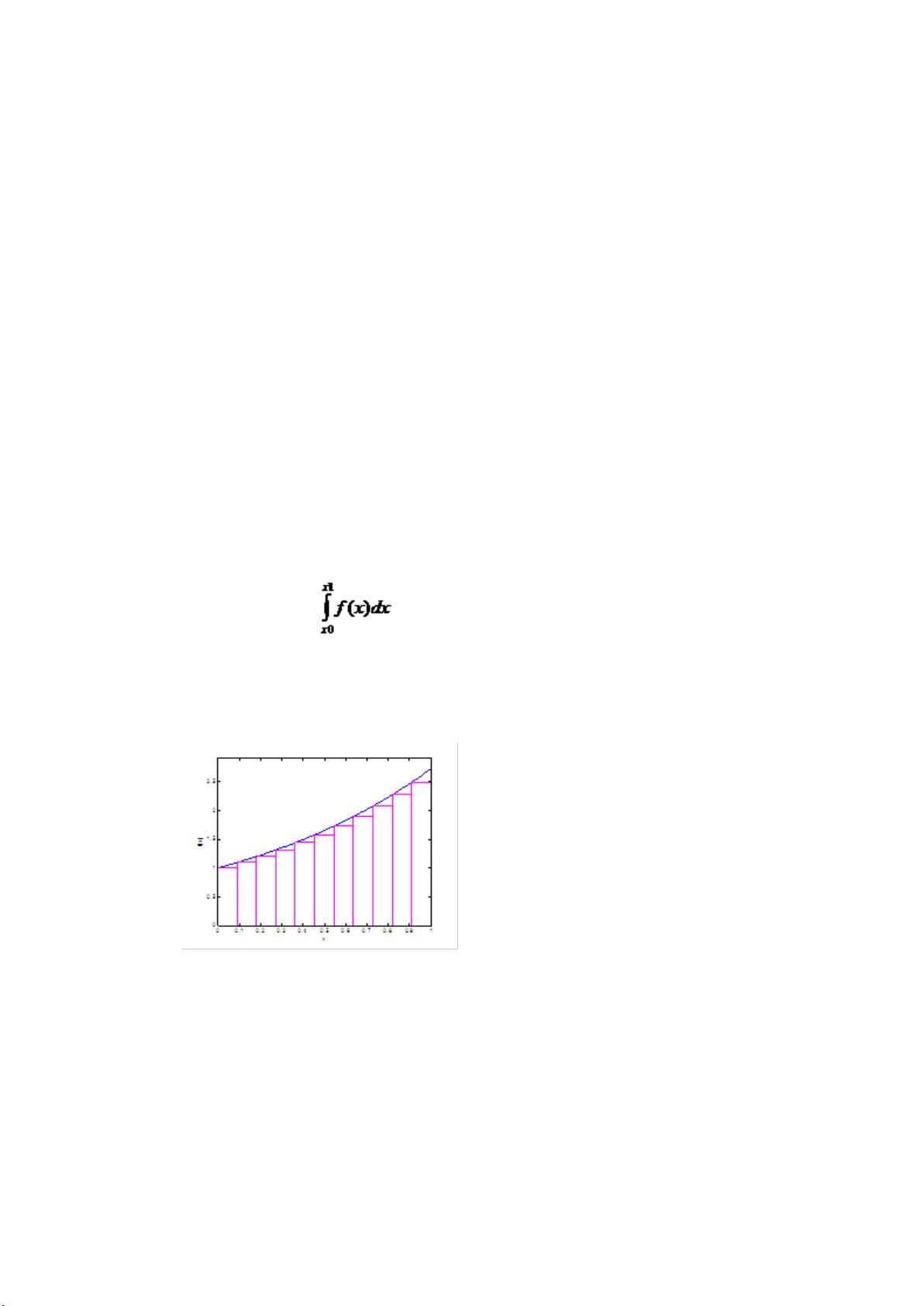
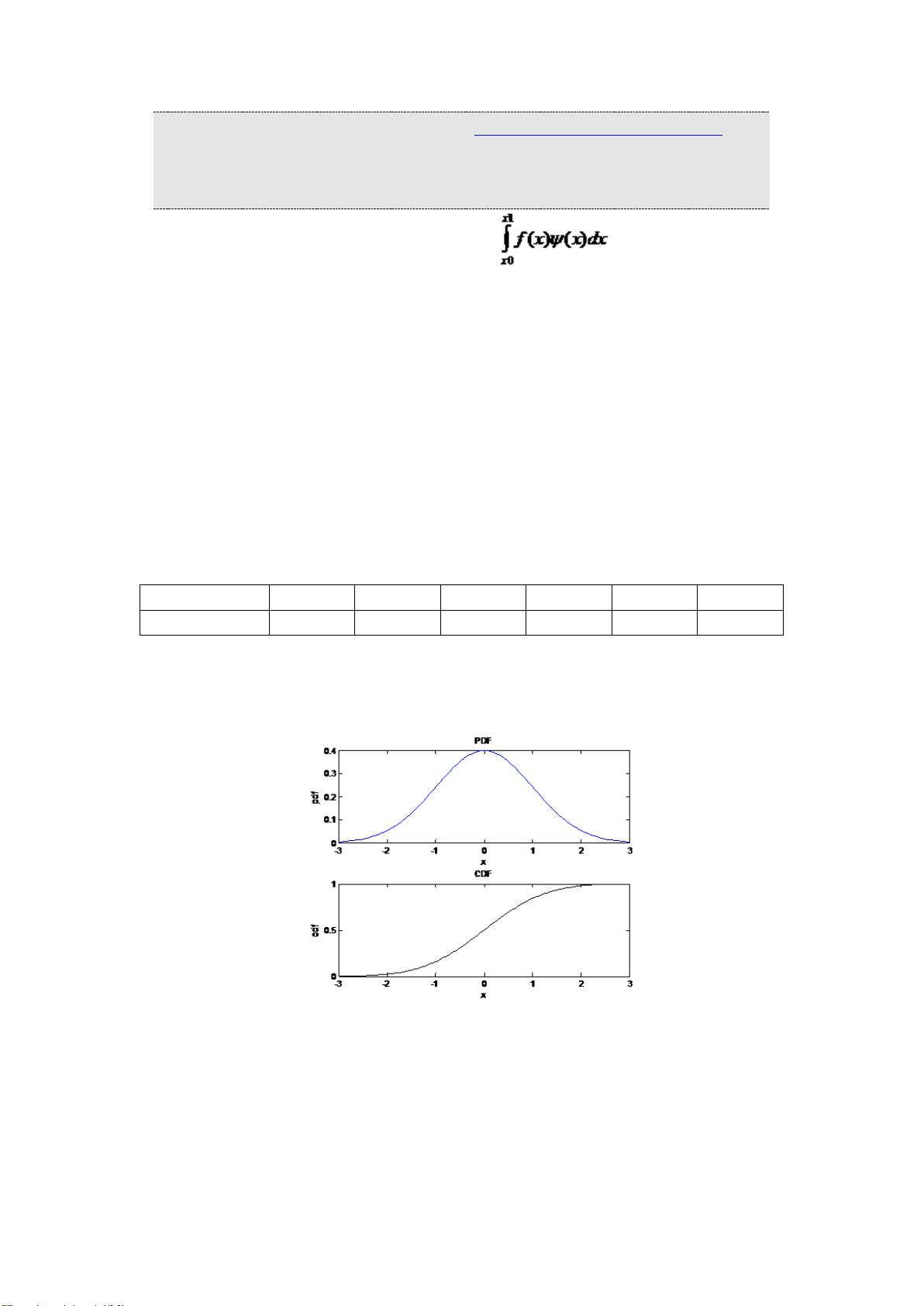
蒙特卡洛算法是一种基于随机抽样和概率统计的数值计算方法，其历史可以追溯到18世纪末，布丰投针试验，这是一种利用随机投掷针来计算圆周率π的方法。20世纪40年代，在美国原子弹计划中，该方法被用来模拟中子的行为，该项目命名为蒙特卡洛，此后该方法名称沿用至今。蒙特卡洛算法与普通的模拟仿真（Simulation）有所区别，在蒙特卡洛算法中，尽管中间计算过程依赖于随机数，但最终结果是确定的。 蒙特卡洛方法最常用的应用领域之一是数值积分计算。传统的数值积分方法通过将积分区间划分为许多小段，然后利用这些小段上的函数值来近似计算总面积。但当函数过于复杂以至于无法求出其原函数时，就需要用数值积分方法进行近似计算。蒙特卡洛数值积分方法利用随机抽样技术来估算积分值，即通过在定义域内随机抽取一些点的函数值，然后累加这些值并计算平均数来近似定积分的值。随着抽取的点数增多，根据大数定律，估算值会越来越接近真实值。 在金融领域，蒙特卡洛方法经常用于计算欧式期权的价格。由于期权的价值依赖于未来可能的价格，而这一价格具有一定的不确定性，通常假设它遵循正态分布或其他概率分布。通过在可能的价格区间内进行大量随机抽样，可以估计期权的期望收益，进而估算期权价值。 此外，蒙特卡洛方法还可以用于随机最优化问题。在最优化问题中，我们希望找到某些函数的最大值或最小值。在随机最优化中，如模拟退火或进化策略等算法，我们可以在函数的定义域内随机选择多个点，然后从中挑选出最优值。例如，若要找到函数的最大值，我们可以从函数的定义域内随机选取若干点，然后比较这些点函数值的大小，取最大的那个函数值作为近似的最大值。这类问题在金融产品定价以外的领域同样存在，但由于在金融中不是特别常用，课程内容没有详细介绍随机最优化方法。 蒙特卡洛方法的一般步骤包括： 1. 根据概率分布生成随机数x，并计算函数f(x)的值。 2. 对所有生成的f(x)值进行累加，并计算平均值。 3. 达到预设的停止条件后终止计算。停止条件可以是生成足够数量的随机数，或计算结果的误差在可接受范围内。 4. 对计算结果进行误差分析，给出点估计的波动程度和区间估计。误差分析是蒙特卡洛方法的一个重要环节，它需要证明结果的收敛性，并计算理论方差。 使用蒙特卡洛算法需要注意的问题包括： - 蒙特卡洛模拟的收敛速度相对较慢，需要大量的随机样本才能获得较为精确的近似值。 - 误差分析必须严格进行，以确保结果的可靠性和精度。 - 蒙特卡洛算法适用的场景通常是那些问题难以用解析方式求解，或者解析解很难获得的情况。 通过应用蒙特卡洛算法，我们可以处理许多涉及随机过程的复杂问题，在数学、物理、工程、金融等领域都有广泛的应用。在实际应用中，为了提高效率和精度，可能需要对算法进行一些改进或与其他数值方法结合使用。