没有合适的资源?快使用搜索试试~ 我知道了~
Support Vector Machines
需积分: 9 4 下载量 115 浏览量
2015-05-31
23:56:56
上传
评论
收藏 187KB PDF 举报
温馨提示
这套笔记介绍了支持向量机(SVM)学习— 算法。支持向量机是最好的(很多人认为是最好的) “现成”的监督学习算法。对支持向量机的故事,我们会 首先要谈的利润与大数据分离的思想 “缺口”。接下来,我们将谈论的最佳间隔分类器,这将导致 我们为拉格朗日对偶题外话。我们也会看到仁,这给 一种应用支持向量机的效率非常高维(例如无限— 维)的特征空间,最后,我们将关闭的故事 SMO算法,给出了支持向量机的高效实现。
资源推荐
资源详情
资源评论

CS229 Lecture notes
Andrew Ng
Part V
Support Vector Machines
This set of notes presents the Support Vector Machine (SVM) learning al-
gorithm. SVMs are among the best (and many believe are indeed the best)
“off-the-shelf” sup ervised learning algorithm. To tell the SVM story, we’ll
need to first talk about margins and the idea of separating data with a large
“gap.” Next, we’ll talk about the optimal margin classifier, which will lead
us into a digression on L agrange duality. We’ll also see kernels, which give
a way t o apply SVMs efficiently in very hig h dimensional (such as infinite-
dimensional) feature spaces, and finally, we’ll close off the story with the
SMO algorithm, which gives an efficient implementation of SVMs.
1 Margins: Intuition
We’ll start our story on SVMs by talking about margins. This section will
give the intuitions about margins and about the “ confidence” of our predic-
tions; these ideas will be made formal in Section 3.
Consider logistic regression, where the probability p(y = 1|x; θ) is mod-
eled by h
θ
(x) = g(θ
T
x). We would then predict “1” on an input x if and
only if h
θ
(x) ≥ 0.5, or equivalently, if and only if θ
T
x ≥ 0. Consider a
positive training example (y = 1 ) . The lar ger θ
T
x is, the larger also is
h
θ
(x) = p(y = 1|x; w, b), and thus a lso the higher our degree of “confidence”
that the label is 1. Thus, informally we can think of our prediction as being
a very confident one that y = 1 if θ
T
x ≫ 0. Similarly, we think of logistic
regression as making a very confident prediction of y = 0, if θ
T
x ≪ 0. Given
a training set, again informally it seems that we’d have found a good fit to
the training data if we can find θ so that θ
T
x
(i)
≫ 0 whenever y
(i)
= 1, and
1
2
θ
T
x
(i)
≪ 0 whenever y
(i)
= 0, since this would reflect a very confident ( and
correct) set of classifications for all the training examples. This seems to be
a nice goal to aim for, and we’ll soon formalize this idea using the notion of
functional margins.
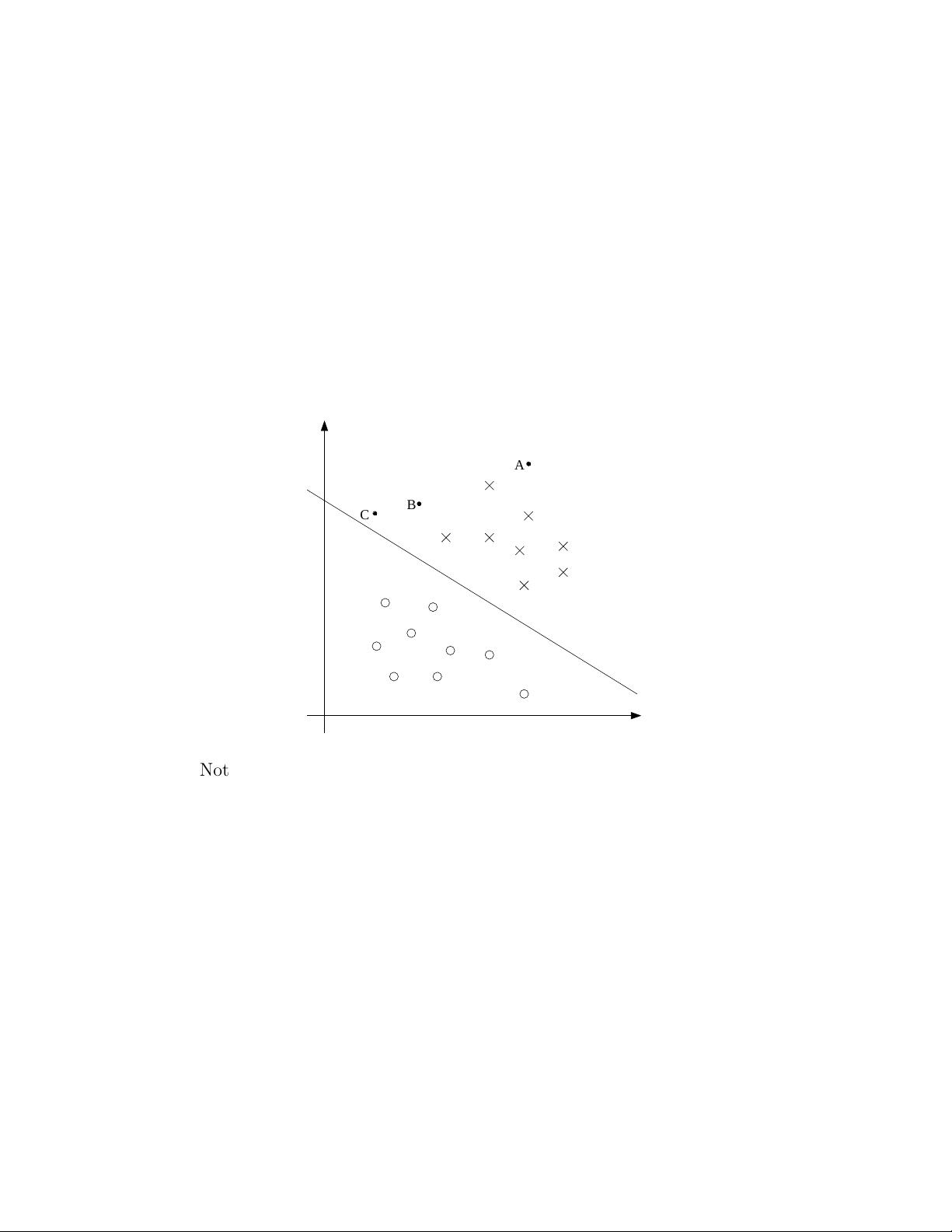
For a different type of int uition, consider the following figure, in which x’s
represent positive training examples, o’s denote negative training examples,
a decision boundary (this is the line given by the equation θ
T
x = 0, and
is also called the separating hyperplane) is also shown, and three point s
have also been labeled A, B and C.
01
01
01
B
A
C
Notice that the point A is very far from the decision boundary. If we are
asked to make a prediction for the value of y at A, it seems we should be
quite confident that y = 1 there. Conversely, the po int C is very close to
the decision boundary, and while it’s on the side of the decision boundary
on which we would predict y = 1, it seems likely that just a small change to
the decision boundary could easily have caused our prediction to be y = 0.
Hence, we’re much more confident about our prediction at A than at C. The
point B lies in-between these two cases, and more broadly, we see that if
a point is far from t he separating hyperplane, then we may be significantly
more confident in our predictions. Again, inf ormally we think it’d be nice if,
given a training set, we manage to find a decision boundary that allows us
to make all correct and confident (meaning far from the decision boundary)
predictions on the training examples. We’ll formalize this later using t he
notion of geometric margins.

3
2 Notation
To make our discussion of SVMs easier, we’ll first need to introduce a new
notation for talking about classification. We will be considering a linear
classifier for a binary classification problem with labels y and features x.
From now, we’ll use y ∈ {−1, 1} (instead of {0, 1}) to denote the class labels.
Also, rather than parameterizing our linear classifier with the vect or θ, we
will use parameters w, b, and write our classifier as
h
w,b
(x) = g(w
T
x + b).
Here, g(z) = 1 if z ≥ 0, and g(z) = −1 otherwise. This “w, b” notation
allows us to explicitly t r eat the intercept term b separately from the other
parameters. (We also drop the convention we ha d previously of letting x
0
= 1
be an extra coordinate in the input feature vector.) Thus, b takes the role of
what was previously θ
0
, a nd w takes the role of [θ
1
. . . θ
n
]
T
.
Note also that, from our definition of g above, our classifier will directly
predict either 1 or −1 (cf. the perceptron algorithm), without first going
through the intermediate step of estimating the probability of y being 1
(which was what logistic regression did).
3 Function al and geometri c margins
Let’s formalize the notions of the functional and geometric margins. Given a
training example (x
(i)
, y
(i)
), we define the functional margin of (w, b) with
respect to the training example
ˆγ
(i)
= y
(i)
(w
T
x + b).
Note that if y
(i)
= 1, then for the functional margin to be large (i.e., for
our prediction to be confident and correct), we need w
T
x + b to be a large
positive number. Conver sely, if y
(i)
= −1, then for the functional margin
to be larg e, we need w
T
x + b to be a larg e negative number. Moreover, if
y
(i)
(w
T
x + b) > 0, then our prediction on this example is correct. (Check
this yourself.) Hence, a la rge functional ma r gin represents a confident and a
correct prediction.
For a linear classifier with the cho ice of g given above (taking values in
{−1, 1}), there’s one property of the functional margin that ma kes it not a
very good measure of confidence, however. Given our choice of g, we note that
if we replace w with 2w and b with 2b, then since g(w
T
x+b) = g(2w
T
x+2b),
4
this would not change h
w,b
(x) at all. I.e., g, and hence also h
w,b
(x), depends
only on the sign, but not on the magnitude, of w
T
x + b. However, replacing
(w, b) with (2w, 2b) also results in multiplying our functional margin by a
factor of 2. Thus, it seems that by exploiting our freedom to scale w and b,
we can make the functional margin arbitrarily large without really changing
anything meaningful. Intuitively, it might therefore make sense to impose
some sort of normalization condition such as that ||w||
2
= 1; i.e., we might
replace (w, b) with (w/||w||
2
, b/||w||
2
), and instead consider the functional
margin of (w/||w||
2
, b/||w||
2
). We’ll come back to this later.
Given a training set S = {( x
(i)
, y
(i)
); i = 1, . . . , m}, we also define the
function margin of (w, b) with respect to S to be the smallest of the functional
margins of t he individual training examples. Denoted by ˆγ, this can therefore
be written:
ˆγ = min
i=1,...,m
ˆγ
(i)
.
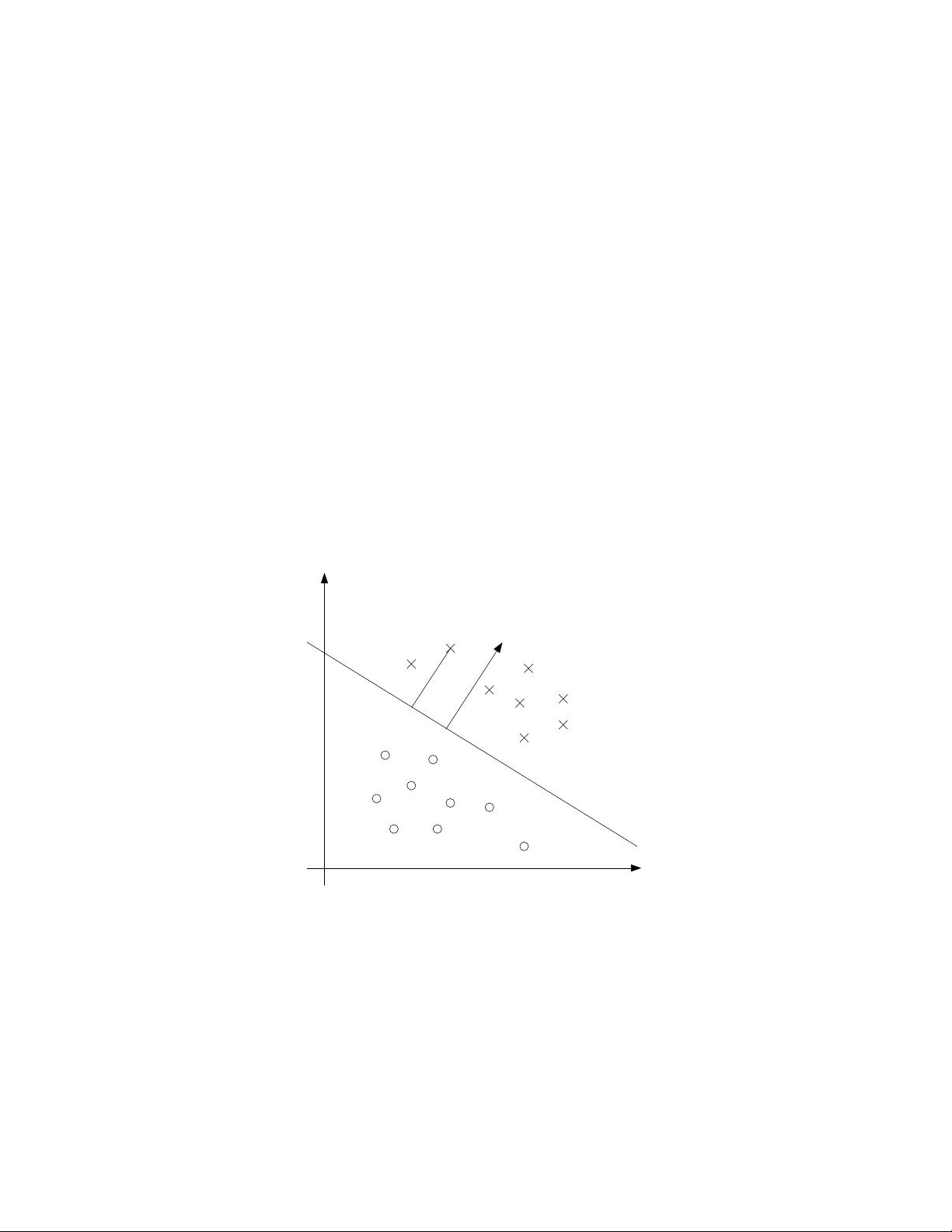
Next, let’s talk about geometric margins. Consider t he picture below:
wA
γ
B
(i)
The decision boundary corresponding to (w, b) is shown, along with the
vector w. Note that w is orthogonal (at 90
◦
) to the separating hyperplane.
(You should convince your self that this must be the case.) Consider the
point at A, which represents the input x
(i)
of some training example with
label y
(i)
= 1. Its distance to the decision boundary, γ
(i)
, is given by the line
segment AB.
How can we find the value of γ
(i)
? Well, w/||w|| is a unit-length vector
pointing in the same direction as w. Since A represents x
(i)
, we therefore
剩余24页未读,继续阅读
资源评论

lhr18716032695
- 粉丝: 0
- 资源: 1
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- Magica Cloth 2 V 2.13布料模拟插件
- 基于SpringBoot的在线考试系统源代码全套技术资料.zip
- 运行在PostgreSQL中的AdventureWorks示例数据库
- 最新女神大秀直播间打赏视频付费观看网站源码 自带直播数据
- 客户购物 (最新趋势) 数据集
- 配电网优化模型matlab 考虑可转移负荷、中断负荷以及储能、分布式能源的33节点系统优化模型,采用改进麻雀搜索算法,以IEEE33节点为例,以风电运维成本、网损成本等为目标,得到系统优化结果,一共有
- MATLAB代码:基于条件风险价值的合作型Stackerlberg博弈微网动态定价与优化调度 关键词:微网优化调度 条件风险价值 合作博弈 纳什谈判 参考文档:A cooperative Stack
- 述职报告PPT模板及样例文章
- MATLAB代码:基于分布式优化的多产消者非合作博弈能量共享 关键词:分布式优化 产消者 非合作博弈 能量共享 仿真平台: matlab 主要内容:为了使光伏用户群内各经济主体能实现有序的电能交易
- 学生抑郁数据集-可以用于分析学生的心理健康趋势
- CRUISE纯电动车双电机四驱仿真模型,基于simulink DLL联合仿真模型,实现前后电机效率最优及稳定性分配 关于模型: 1.策略是用64位软件编译的,如果模型运行不了请将软件切成64位 切
- Android程序开发初级教程WORD文档doc格式最新版本
- cruise混动仿真,P2并联混动仿真模型,Cruise混动仿真模型,可实现并联混动汽车动力性经济性仿真 关于模型 1.模型是基于cruise simulink搭建的base模型,策略模型基于MAT
- HCIP 复习内容实验 ia
- BGP路由协议模拟器,网络路由条目实时监控
- MATLAB代码:含多种需求响应及电动汽车的微网 电厂日前优化调度 关键词:需求响应 空调负荷 电动汽车 微网优化调度 电厂调度 仿真平台:MATLAB+CPLEX 主要内容:代码主要做的是一
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功