17J_LocalizationofsoundsourcesinroboticsAreview_麦克风阵列声源测向入门综述.pdf资源-CSDN文库

需积分: 9 60 浏览量 2019-09-01 08:39:44 上传评论 1 收藏 1.36MB PDF 举报

### 声源定位在机器人技术中的应用综述 #### 概述本文献综述主要探讨了声源定位（Sound Source Localization,简称SSL）在机器人领域的应用与进展。声源定位是通过声学信号自动估计声音来源位置的技术，对于机器人而言，这项技术至关重要，它不仅能够帮助机器人定位说话人的位置，还能够在没有视觉辅助的情况下识别和定位环境中的声音事件。该文献深入分析了SSL在机器人平台上的应用，并概述了SSL技术的发展历程、分类、评估方法及其面临的挑战。 #### 声源定位技术的历史与演变声源定位技术最初起源于军事领域，用于检测和定位远处的声音信号，例如炮火或敌机的声音。随着技术的进步和需求的变化，声源定位逐渐被应用于民用领域，特别是在机器人技术中发挥着重要作用。文献回顾了声源定位技术从早期发展至今的过程，包括各种算法和技术的演进，以及这些技术如何逐步适应于不同的机器人平台。 #### SSL技术分类文章中提到了几种常见的声源定位技术，并对其进行了详细的分类： 1. **基于方向到达（Direction of Arrival, DOA）的方法**：这种方法利用麦克风阵列接收的声音信号之间的相位差或时间差来确定声源的方向。 2. **基于距离估计算法**：这类技术通常涉及到多普勒效应等原理，通过测量声波传播的时间或者频率变化来计算声源与麦克风之间的距离。 3. **跟踪算法**：除了静态声源定位外，还有一些技术专注于动态声源的追踪。这些算法通常结合了机器学习和计算机视觉技术，以便更准确地预测和跟踪移动声源的位置。 #### SSL问题的不同方面声源定位问题不仅仅局限于简单的方向或距离估计，还包括了一系列复杂的问题，如噪声抑制、回声消除、多声源分离等。这些问题对实际应用构成了挑战，同时也促进了技术的发展。文献中详细介绍了这些不同方面的内容，并讨论了它们如何相互作用以提供更精确的定位结果。 #### SSL性能评估方法为了确保声源定位系统的有效性，研究人员开发了多种评估方法。这些方法通常包括实验设计、性能指标定义及测试环境设置等。文献中列举了一些常用的评估标准，比如定位精度、响应时间和鲁棒性等，并探讨了它们在不同应用场景下的适用性。 #### 当前挑战与未来研究方向尽管声源定位技术已经取得了显著进步，但仍存在许多未解决的问题和挑战，如在嘈杂环境中提高定位准确性、降低系统复杂度等。文献最后部分讨论了当前面临的一些挑战，并提出了一些潜在的研究方向，旨在推动声源定位技术在未来的发展。 #### 结论声源定位技术在机器人领域具有广泛的应用前景，从改善人机交互到增强机器人的感知能力，都是其重要的应用场景。通过对现有技术和研究成果的综合分析，本文为读者提供了关于声源定位在机器人中应用的全面理解，并为未来的科研工作指明了方向。

资源推荐

资源详情

资源评论

Robotics and Autonomous Systems 96 (2017) 184–210

Contents lists available at ScienceDirect

Robotics and Autonomous Systems

journal homepage: www.elsevier.com/locate/robot

Localization of sound sources in robotics: A review

Caleb Rascon *, Ivan Meza

Instituto de Investigaciones en Matematicas Aplicadas y en Sistemas, Universidad Nacional Autonoma de Mexico, Circuito Escolar S/N, Mexico 04510,

Mexico

h i g h l i g h t s

• A highly detailed survey of sound source localization (SSL) used over robotic platforms.

• Classification of SSL techniques and description of the SSL problem.

• Description of the diverse facets of the SSL problem.

• Survey of the evaluation methodologies used to measure SSL performance in robotics.

• Discussion of current SSL challenges and research questions.

a r t i c l e i n f o

Article history:

Received 18 August 2016

Received in revised form 24 June 2017

Accepted 21 July 2017

Available online 5 August 2017

Keywords:

Robot audition

Sound source localization

Direction-of-arrival

Distance estimation

Tracking

a b s t r a c t

Sound source localization (SSL) in a robotic platform has been essential in the overall scheme of robot

audition. It allows a robot to locate a sound source by sound alone. It has an important impact on

other robot audition modules, such as source separation, and it enriches human–robot interaction by

complementing the robot’s perceptual capabilities. The main objective of this review is to thoroughly

map the current state of the SSL field for the reader and provide a starting point to SSL in robotics. To

this effect, we present: the evolution and historical context of SSL in robotics; an extensive review and

classification of SSL techniques and popular tracking methodologies; different facets of SSL as well as its

state-of-the-art; evaluation methodologies used for SSL; and a set of challenges and research motivations.

(http://creativecommons.org/licenses/by/4.0/).

1. Introduction

The goal of sound source localization (SSL) is to automatically

estimate the position of sound sources. In robotics, this function-

ality is useful in several situations, for instance: to locate a human

speaker in a waiter-type task, in a rescue scenario with no visual

contact, or to map an unknown acoustic environment. Its perfor-

mance is of paramount influence to the rest of a robot audition

system since its estimations are frequently used in subsequent

processing stages such as sound source separation, sound source

classification and automatic speech recognition.

There are two components of a source position that can be

estimated as part of SSL (in polar coordinates):

• Direction-of-arrival estimation (which can be in 1 or 2 di-

mensions)

• Distance estimation.

Corresponding author.

E-mail addresses: caleb.rascon@iimas.unam.mx (C. Rascon),

ivanvladimir@turing.iimas.unam.mx (I. Meza).

SSL in real-life scenarios needs to take into account that more

than one sound source might be active in the environment. There-

fore it is also necessary to estimate the position of multiple simul-

taneous sound sources. In addition, both the robot and the sound

source are mobile, so it is important to track its position through

time.

SSL has been substantially pushed forward by the robotics com-

munity by refining traditional techniques such as: single direction-

of-arrival (DOA) estimation, learning-based approaches (such as

neural network and manifold learning), beamforming-based ap-

proaches, subspace methods, source clustering through time and

tracking techniques such as Kalman filters and particle filtering.

While implementing these techniques onto robotics platforms,

several facets relevant to SSL in robots have been made evident

including: number and type of microphones used, number and

mobility of sources, robustness against noise and reverberation,

type of array geometry to be employed, type of robotic platforms

to build upon, etc.

As it is shown in this review, the SSL field in robotics is quite

mature, proof of which are the recent surveys in this topic. For

instance, [1,2] present a survey on binaural robot audition, [3]

offers a general survey of SSL in Chinese, [4] presents some SSL

http://dx.doi.org/10.1016/j.robot.2017.07.011

红色下划线：重要观点句

绿色高亮；关键词

黄色高亮：不认识的单词

C. Rascon, I. Meza / Robotics and Autonomous Systems 96 (2017) 184–210 185

works based on binaural techniques and multiple-microphone

arrays, and [5] presents an overview of the robot audition field

as a whole. The aim of this work is to review the literature of

SSL implemented over any type of robot, such as service, rescue,

swarm, industrial, etc. We also review efforts that are targeted for

an implementation in a robotic platform, even if they were not

actually implemented in one. In addition, we review resources for

SSL training or evaluation, including some that were not collected

from a robotic perspective but could be applied to a robotic task.

Finally, we incorporate research that uses only one microphone for

SSL that, although not applied in a robotic platform, we believe has

an interesting potential for the SSL robotic field.

In this work we present: the evolution of the field (Section 2);

a definition of the SSL problem (Section 3); a classification of tech-

niques used in SSL within the context of robot audition (Section 4);

an overview of popular tracking techniques used for SSL (Sec-

tion 5); several facets that describe the areas that SSL techniques

are tackling (Section 6); a review of different evaluation methods

that are currently being used for measuring the performance of SSL

techniques (Section 7); and an insight on potentially interesting

challenges for the community (Section 8). Finally, we highlight

several motivations for future research questions in the robot

audition community (Section 9).

2. The evolution of SSL

The surge of SSL in robotics is relatively new. To our knowledge,

it started in 1989 with the robot Squirt, which was the first robot to

have a SSL module [6,7]. Squirt was a tiny robot with two compet-

ing behaviors: hiding in a dark place and locating a sound source.

The idea of using SSL as a behavior to drive interaction in a robot

was later explored by Brook’s own research team and it culminated

with a SSL system for the Cog robot [8–11]. In the meantime,

several Japanese researchers started to investigate the potential

of SSL in a robot as well. In 1993, Takanashi et al. explored an

anthropomorphic auditory system for a robot [12,13] (as described

by [10]). This research was followed by notable advances in the

field: Chiye robot [14], RWIB12-based robot [15–18], Jijo-2 [19,20],

Robita [21] and Hadalay [22]. This first generation of robots tackled

difficult scenarios such as human–robot interaction, integrating

a complete auditory system (source separation feeding speech

recognition), active localization, dealing with mobile sources and

capture systems, and by exploring different methodologies for

robust SSL.

At the turn of the 20th century, the binaural sub-field of robot

audition started to become an important research effort, including

SSL. Although robots from the first generation were technically

binaural (e.g., Squirt, COG, Chiye, Hadalay), it is with the arrival of

the SIG robot [23] that the field of binaural robot audition started

to generate interest. SIG was built to promote audition as a basic

skill for robots and was presented as an experimental platform for

the RoboCup Humanoid Challenge 2000 [24]. This resulted in SIG

becoming popular for researching robot perception. Binaural robot

audition has been followed by other research teams and progress

in the field has been constant [25–36].

During the 2000s, an important rift occurred in terms of the

research motivations in the robot audition field, specifically in SSL

techniques. Binaural audition cemented itself by the motivation

to imitate nature: using only two ears/microphones. On the other

hand, there was the motivation to increase performance (detailed

in Section 4.3), which pushed for the use of more microphones.

This opened the door for source localization techniques that use

a high amount of sensors (such as MUSIC and beamformers) to

carry out SSL in a robot. Subsequently, the facets of the SSL problem

were broadened, which yielded a wide variety of solutions from the

robot audition community.

Fig. 1. The complete data pipeline of an end-to-end SSL methodology.

Throughout its history, a central goal for robots with a SSL

system has been to support interaction with humans. In the first

generations, an important contribution was to face the user, since

it indicates that the robot is paying attention. One of the first

robots to carry out this attention-based interaction was the Chiye

robot [14] which has made its way into recent products such

as the Paro robot [37]. Further on, SSL has been used in more

complex settings in which other skills intertwine together to reach

a specific goal, such as: playing the Marco-Polo game, acting as a

waiter, taking assistance and finding its user when it visually lost

him/her [38]; logging and detecting the origin of certain sounds

while interacting with a caregiver [39]; playing a reduced version

of hide and seek in which hand detection and SSL are used to guide

the game [40]; providing visual clues from the sound sources as a

complement of a telepresence scenario [41]; and directing a trivia-

style game [42]. Given the evolution of SSL in robots, we are certain

that the complexity of the scenarios will keep growing. In fact,

we foresee that the challenges to come will definitely be more

demanding (see Section 8 for further discussion).

3. Definition of the sound source localization problem

Sound source localization (SSL) tackles the issue of estimating

the position of a source via audio data alone. This generally involves

several stages of data processing. Its pipeline is summarized in

Fig. 1.

Since this pipeline receives the data directly from the micro-

phones and provides a SSL estimation, we consider a methodology

that carries this out as end-to-end. Features are first extracted from

the input signals. Then, a feature-to-location mapping is carried

out, which usually relies on a sound propagation model. These

three phases are referenced as such in the explanation of each

methodology and their relevant variations in Section 4.

In this section a brief overview of these three phases is pre-

sented for ease of reference in the later detailed explanations.

3.1. Propagation models

The sound propagation model is proposed depending on: the

positioning of the microphones, as there may be an object between

them; the robotic application, as the user may be very close or far

away from the microphone array; and the room characteristics,

as they define how sound is reflected from the environment. In

addition, the propagation model generally dictates the type of

features to be used.

The most popular propagation model used is the free-field/far-

field model, which assumes the following:

• Free field: The sound that is originated from each source

reaches each microphone via a single, direct path. This

186 C. Rascon, I. Meza / Robotics and Autonomous Systems 96 (2017) 184–210

means that there are no objects between the sources and

the microphones and that there are no objects between the

microphones. In addition, it is assumed that there are no

reflections from the environment (i.e., no reverberation).

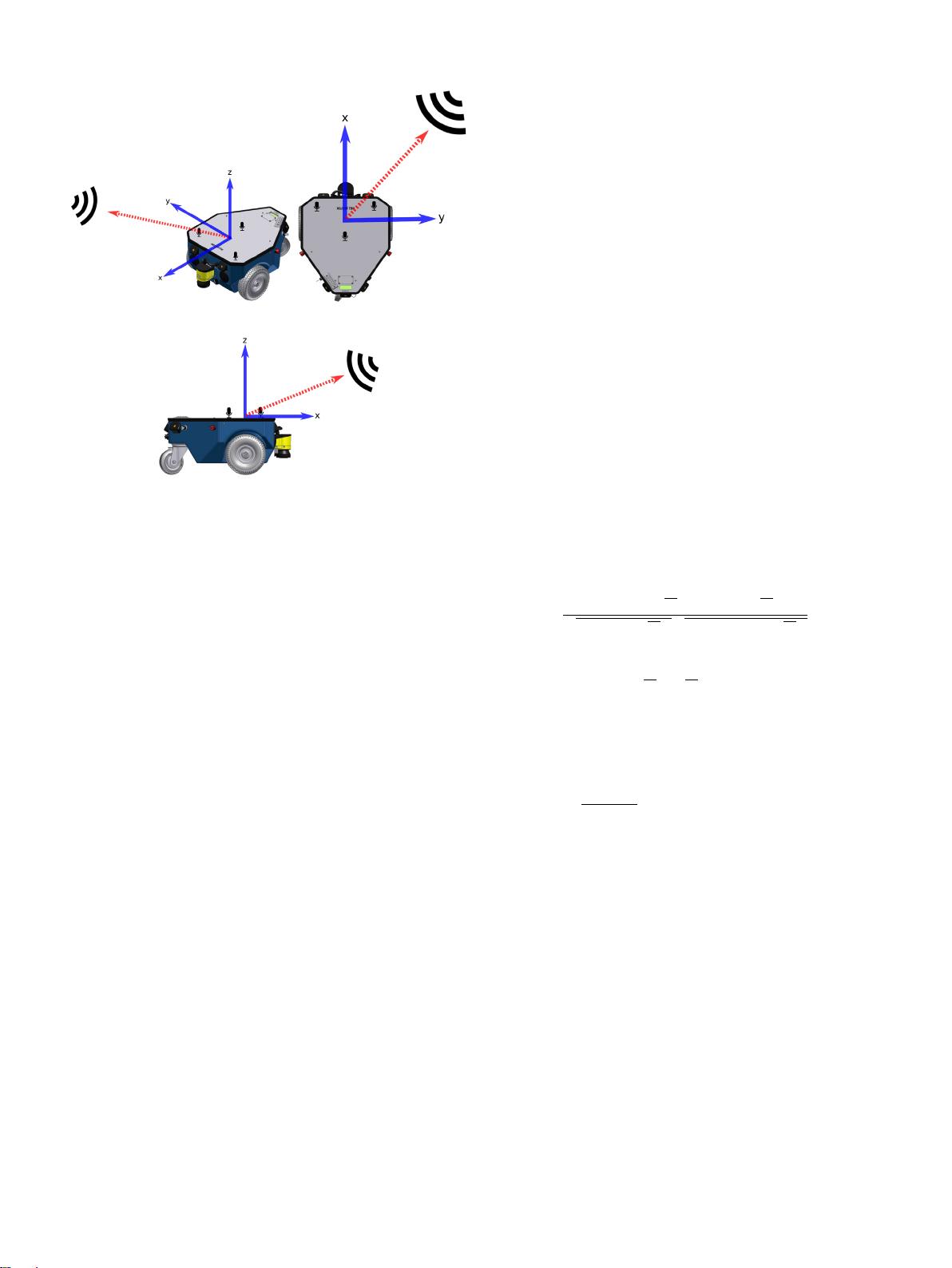
• Far field: The relation between the inter-microphone dis-

tance and the distance of the sound source to the micro-

phone array is such that the sound wave can be considered

as being planar.

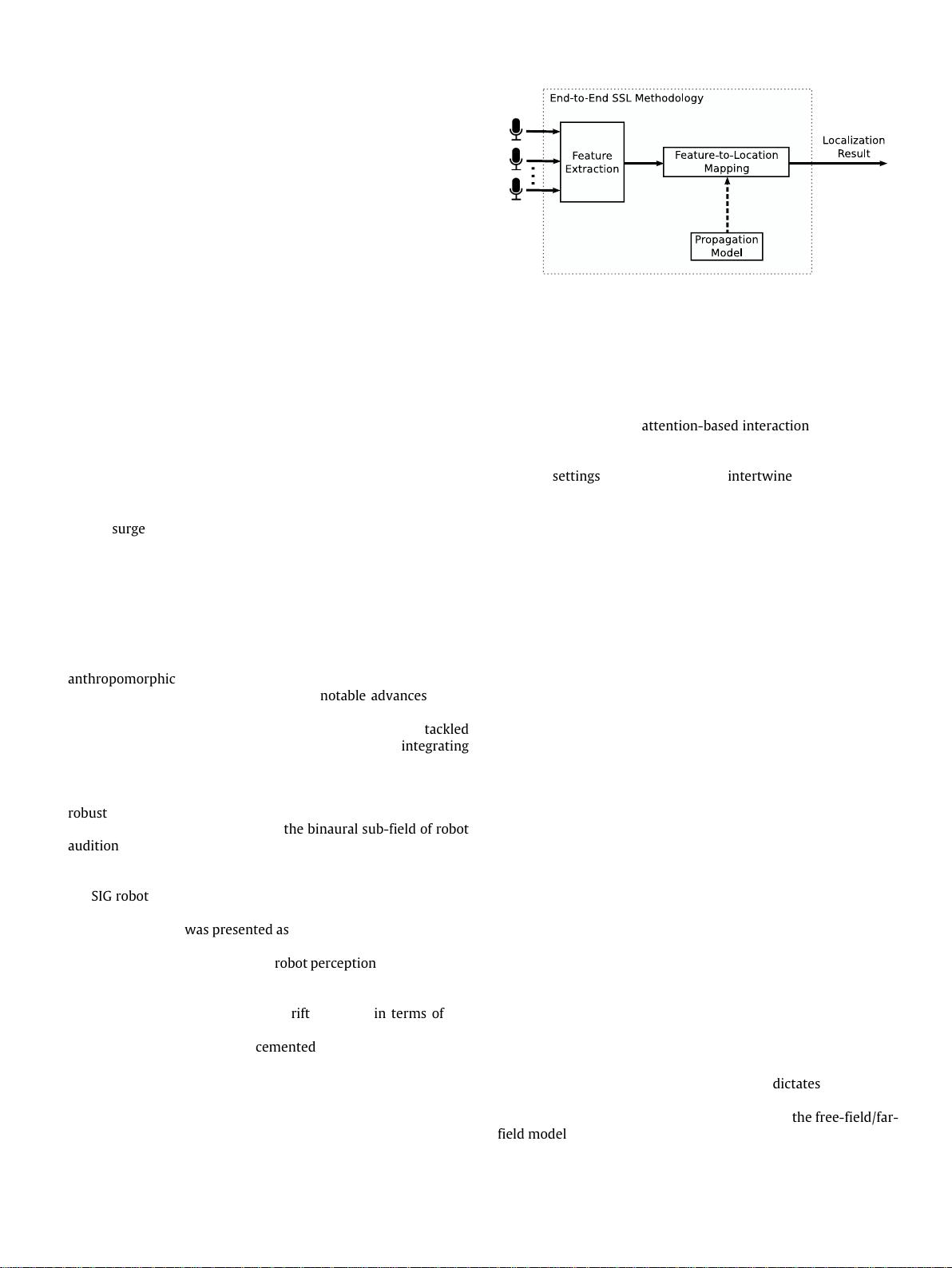
The second assumption greatly simplifies the mapping proce-

dure between feature and location, as discussed in Section 4.1.

There are other type of propagation models that are relevant

in SSL in robotics. The Woodworth–Schlosberg spherical head

model [43, pp. 349–361] has been used extensively in binaural

arrays placed on robotic heads [23,44] and is explained in Sec-

tion 4.2. The near-field model [45] assumes that the user can be

near the microphone array, which requires to consider the sound

wave as being circular. There are a few robotic applications that use

the near-field model, such as [46], however it is not as commonly

used as the far-field model. In fact, there are approaches that

use a modified far-field model successfully in near-field circum-

stances [47] or that modify the methodology design to consider

the near-field case [48]. Nevertheless, as presented in [48], a far-

field model directly used in near-field circumstances can decrease

the SSL performance considerably. In addition, there are cases

in which the propagation model is learned, such as the neural-

network-based approaches in [49,50], manifold learning [33,51],

linear regression [52] and as part of a multi-modal fusion [11,21].

3.2. Features

There are several acoustic features used throughout the re-

viewed methodologies. In this section, we provide a brief overview

of the most popular:

Time difference of arrival (TDOA). It is the time-difference be-

tween two captured signals. In 2-microphone arrays (binaural

arrays) that use external pinnae, this feature is also sometimes

called the inter-aural time difference (ITD). There are several

ways of calculating it, such as measuring the time difference be-

tween the moments of zero-level-crossings of the signals [18] or

between the onset times calculated from each signal [6,7,14,17].

Another way to calculate the TDOA is by assuming the sound

source signal is narrowband. Let us denote the phase difference

of two signals at frequency f as 1ϕ

. If f

is the frequency with

the highest energy, the TDOA for narrowband signals (which

is equivalent to the inter-microphone phase difference, or IPD)

can be obtained by

1ϕ

2πf

[23]. However, the most popular way

of calculating the TDOA as of this writing is based on cross-

correlation techniques, which are explained in detail in Sec-

tion 4.1.

Inter-microphone intensity difference (IID). It is the difference

of energy between two signals at a given time. This feature,

when extracted from time-domain signals, can be useful to

determine if the source is in the right, left or front of a

2-microphone array. To provide greater resolution, a many-

microphone array is required [53] or a learning-based mapping

procedure can be used [10]. The frequency-domain version

of IID is the inter-microphone level difference (ILD) that is

provided as the difference spectrum between the two short-

time-frequency-transformed captured signals. This feature is

also often used in conjunction with a learning-based mapping

procedure [35].

A similar feature to the ILD are the set of differences of the

outputs of a set of filters spaced logarithmically in the frequency

domain (known as a filter bank). These set of features have

shown more robustness against noise than the IID [9], while

employing a feature vector with less dimensions than the ILD.

In [54], the ILD is calculated in the overtone domain. A

frequency f

is an overtone of another f when f

= rf (given that

r ∈ [2, 3, 4, . . .]) and their magnitudes are highly correlated

through time. This approach has the potential of being more

robust against interferences, since the correlation between the

frequencies implies they belong to the same source.

Spectral notches. When using external pinnae

or inner-ear

canals, there is a slight asymmetry between the microphone

signals. Because of this, the result of their subtraction presents

a reduction or amplification in certain frequencies, which de-

pend on the direction of a sound source. These notches can

be mapped against the direction of the sound source by ex-

perimentation [52]. However, because small changes to the

external pinnae may hinder the results from these observations,

it is advisable to use learning-based mapping when using these

features [49].

Binaural/spectral cues. It is a popular term to refer to the feature

set that is composed by the IPD and the ILD in conjunction. This

feature set is often used with learning-based mapping [50,51].

They are often extracted on an onset to reduce the effect of

reverberation [55]. It has been shown in practice that temporal

smoothing of this feature set makes the resulting mapping more

robust against moderate reverberation [56].

Besides these features, there are others that are also highly used,

such as the MUSIC pseudo-spectrum and the beamformer steered-

response. However, their application is bound to specific end-to-

end methodologies. Because of this, their detailed explanation is

given in Section 4.

3.3. Mapping procedures

A mapping procedure for SSL is expected to map a given ex-

tracted feature to a location. A typical manner to carry this out

is by applying directly the propagation model, such as the free-

field/far-field model or the Woodworth–Schlosberg spherical head

model, both discussed in Section 3.1. However, there are some

type of features (especially those used for multiple-source-location

estimation) which require an exploration or optimization of the

SSL solution space. A common approach is to carry out a grid-

search, in which a mapping function is applied throughout the SSL

space and the function output is recorded for each tested sound

source location. This produces a solution spectrum in which peaks

(or local maximums) are regarded as the SSL solutions. This is the

most used type of mapping procedure for multiple-source-location

estimation. Two important examples are the subspace orthogonal-

ity feature of MUSIC and the steered-response of a delay-and-sum

beamformer. These are detailed further in Section 4.3.

There are types of mapping procedures other than grid-search.

Their main focus is to train the mapping function based on

recorded data of sources with known locations. As a result, the

mapping function that was learned implicitly encodes the prop-

agation model. In this survey, this type of mapping procedures are

referred to as learning-based mapping. These are based in differ-

ent training methodologies, such as neural networks [11,21,49],

locally-linear regression [57], manifold learning [33,51], etc. Fur-

ther details are given of each mapping procedure in the relevant

branches of the methodology classification presented in Section 4.

External ears.

这块主要列

举了几种用

来计算到达

时间差的方

法

C. Rascon, I. Meza / Robotics and Autonomous Systems 96 (2017) 184–210 187

(a) Full frame of reference. (b) Azimuth (top view).

Fig. 2. Graphical representation of the most used frame of reference. Based on the

CAD views of the Neobotix MP-500 mobile robot [58].

4. Classification of sound source localization end-to-end

methodologies

As mentioned before, the location of a sound source is usually

considered as being composed of two parts: (1) the direction of

arrival (DOA) of the source and (2) the distance of the source to the

microphone array. The frame of reference that is used by most (if

not all) of the reviewed works is exemplified in Fig. 2, which shows

a robot mounted with a 3-microphone array.

As it can be seen, the center of the microphone array is generally

considered as the origin. The azimuth plane (presented in Fig. 2b) is

parallel to the horizon of the physical world and the elevation plane

(presented in Fig. 2c) is orthogonal to it. This is the terminology and

frame of reference used throughout the survey.

In this section, a classification of end-to-end methodologies

used for SSL by the robotics community is presented. Because of

the two-part composition of a sound source location, a type of

divide-and-conquer philosophy of SSL has become popular: the

estimation of the DOA and the distance is carried out separately.

And, in most cases, the DOA is usually the only part of the loca-

tion reported. Given this popularity, this section mostly reviews

methodologies that estimate the DOA of the sound source. How-

ever, important advances in distance estimation have been made,

which warrants their own branch.

The presented classification is summarized as follows:

• 1-dimensional single direction-of-arrival estimation. In

this branch, techniques that estimate the DOA in the az-

imuth plane of a single source are described.

• 2-dimensional single direction-of-arrival estimation. In

this branch, techniques that estimate the DOA in both the

azimuth and the elevation plane of a single source are de-

scribed.

• Multiple direction-of-arrival estimation. In this branch,

techniques that estimate the DOA of multiple sources are

described. These are mostly in the azimuth plane, but the

process of how to generalize them into both planes is also

described. This branch is further divided into three sub-

branches:

– Beamforming-based. Those that carry out spatial filter-

ing towards several DOA candidates.

– Subspace methods. Those that take advantage of the

differentiation between signal and noise subspaces.

– Source clustering through time. Those that carry out sin-

gle DOA estimation throughout various time windows

and provide a multiple-DOA solution by clustering

these results.

• Distance estimation. In this branch, techniques that esti-

mate the distance of the sound source to the microphone

array are described.

The full list of the 188 reviewed works has been made available

through an Excel file that is part of the additional external material

that comes with this writing.

4.1. 1-dimensional single direction-of-arrival estimation

There are many works whose objective is to locate and track one

sound source in the environment. A very commonly used feature

to achieve this objective is the time-difference-of-arrival (TDOA)

between a pair of sensors or microphones. The most popular way to

estimate the TDOA as of this writing is based on calculating a cross-

correlation vector (CCV ) between two captured signals. One of the

simplest way to calculate CCV is based on the Pearson correlation

factor, as presented in Eq. (1):

CCV [τ] =



[t] − x

)(x

[t − τ ] − x

)





[t] − x

)





[t − τ ] − x

)

(1)

where x

and x

are the two discrete signals being compared; τ is

the point at which x

is being linearly shifted and the correlation

is being calculated; and x

and x

are the mean values of x

and x

respectively. The TDOA of the sound source (τ

) is the τ value that

maximizes CCV . As mentioned before, the free-field/far-field prop-

agation model is the most commonly used (presented in Eq. (2))

and it provides a simple feature-to-location mapping between τ

and the DOA of the source (θ

= arcsin



sound

· τ

sample

· d



(2)

where V

sound

is the speed of sound (∼343 m/s); f

sample

is the sam-

pling frequency in Hz; d is the distance between microphones in

meters; and τ

is the TDOA of the sound source in number of sam-

ples. To simplify SSL in real-life environments, the microphones are

positioned such that the imaginary line between them is parallel

to the azimuth plane, resulting in θ

being the DOA in that plane.

If elevation is required, the microphone pair can be positioned

such that they cross the elevation plane. However, only the DOA

in the plane of the microphone array is able to be estimated by this

methodology.

Estimating the TDOA via CCV can be very sensitive to reverber-

ations and other noise sources [59, pp. 213–215]. In these cases,

correlation values are ‘‘spread’’ into other TDOAs [60], resulting in

wide hills of correlation as well as TDOA estimation errors [61]. To

counter this, a similar correlation vector can be calculated by an

alternative approach. A frequency-domain-based cross-correlator

(CC

) [62] is presented in Eq. (3):

[f ] = X

[f ]X

[f ]

∗

(3)

where X

and X

are the Fourier transforms of x

and x

of Eq. (1)

respectively; the {.}

∗

operator stands for the complex conjugate

188 C. Rascon, I. Meza / Robotics and Autonomous Systems 96 (2017) 184–210

operation; and CC

is a frequency-domain-based cross-correlator.

It is important to state that the resulting F

−1

(CC

) presents the cor-

relation information in a different manner than CCV . However, the

peaks in F

−1

(CC

) are found in the same places of high correlation

as in CCV in the range of −τ

max

≤ τ ≤ τ

max

, where τ

max

is the

maximum value of τ that can physically occur.

By performing this operation in the frequency domain, a

weighting function ψ[f ] can be applied as in Eq. (4), which is

known as generalized cross-correlation (GCC) [60]:

GCC

[f ] = ψ[f ]X

[f ]X

[f ]

∗

. (4)

ψ[f ] varies depending on the objective of the correlation vector.

If ψ[f ] = 1, the resulting F

−1

(GCC

) equates to F

−1

(CC

) which

suffers from sensitivity to reverberation, similar to CCV calculated

by Eq. (1). Therefore, it is of interest that Dirac delta functions

appear in the correlation vector only in places of high correla-

tion. Since the Fourier transform of a Dirac delta function has all

frequency magnitudes at 1, normalizing the magnitudes in GCC

forces the presence of approximations of Dirac delta functions in

places of high correlation. To normalize these magnitudes, ψ [f ] is

equated to the inverse of the magnitude of the signal multiplica-

tion, as in Eq. (5):

ψ[f ] =

[f ]X

[f ]

∗

. (5)

By applying ψ[f ] in Eq. (4), the phase information is left intact in

GCC

, thus ψ[f ] of Eq. (5) is known as the phase transform (PHAT ).

The generalized cross-correlation with phase transform [60] (GCC-

PHAT) is presented in Eq. (6):

PHAT

[f ] =

[f ]X

[f ]

∗

[f ]X

[f ]

∗

. (6)

Carrying out this normalization is equivalent to ‘‘whitening’’

the input signals, since all frequencies have a magnitude of 1. This

has been shown to produce a ‘‘spikier’’ crosspower spectrum [63].

Because of this, interfering sources produced by either actual

sound sources or environmental reflections (i.e., reverberation)

tend to also ‘‘appear’’ as other peaks in the correlation vector. This

offsets their effect on the correlation calculations in other TDOAs,

which is not the case with the Pearson-based method described by

Eq. (1). This provides GCC-PHAT robustness against reverberation,

as shown via simulation in [61]. It also provides robustness against

interfering sources in high signal-to-interference ratio (SIR) cir-

cumstances, as shown in a multiple source scenario in [64].

The PHAT weighting function is typically applied uniformly

throughout the frequency bins which introduces sensitivity to

broadband noise sources. To counter this, the PHAT weighting

function can be modified such that additional weights are set

depending on the ‘‘noisiness’’ of the frequency bins. Good examples

of this are presented in [47,65,66], where an additional weight-

ing term is added to the PHAT weighting function based on the

frequency bin SNR, providing robustness against noise. However,

applying non-zero weights to the frequency bin may produce noise

leaking into other frequencies. To avoid this, an evolution of this

approach is presented in [67], where a hard binary mask is applied

instead. Meaning, only binary weights are added to the PHAT

weighting function: 1 if the SNR is above a certain threshold, 0

otherwise. Unfortunately, using these hard masks results in leaks

in the DOA estimation with unwanted dominant peaks. This issue

is countered in [68], where a transition mask is used between noise

and speech windows.

Which happens when the sound source is placed in the imaginary line that

crosses both microphones. That is to say, when θ = 90

◦

. Thus, it is calculated as

max

sample

·d

sound

sin(90

◦

It is important to mention that these masking methods require

on-line noise estimation to calculate the narrowband SNRs for each

frequency. An alternative to this is to create a binary mask that only

nullifies the frequency bins outside the frequency range used by

the type of source the application calls for. In the case of [69], the

authors aimed to track only speech sources, thus all frequency bins

outside the frequency range of voice were nullified.

GCC-PHAT is probably the most commonly used TDOA estima-

tion technique for single direction-of-arrival estimation in robot

audition because of its robustness and its ease of implementation.

For example, in [70,71], GCC-PHAT is used to carry out an acoustic

map of the environment via an exploration carried out by a robot.

Other works that use GCC-PHAT as part of their sound source

localization systems for service robots can be found in [28,72–76].

Interestingly, the appearance of peaks in PHAT bins other

than the one representing the signal of interest may constitute

other sources which are assumed as interfering. Because of this,

some proposals use PHAT as a simple way to estimate multiple

directions-of-arrival [64,77]. However, even with the changes to

ψ[f ] to make it applicable, the appearance of peaks is dependent

on the ratio of power between the multiple sources [64]. As far as

we know, this variation of the GCC-PHAT technique has not been

applied in the context of robot audition.

As mentioned before, the free-field/far-field propagation model

is the most commonly used for single-DOA estimation, however

other sound propagation models can be used for 1-dimensional

single-DOA estimation. In [78], a spherical head is assumed to be

positioned between the microphones. For this purpose, the authors

use the Woodworth–Schlosberg head model [43, pp. 349-361],

shown in Eq. (7):

τ (θ ) =

sound

(θ + sin(θ )) (7)

where d/2 represents the radius of the head. Two propagation

paths are then observed: one that propagates through the front of

the head and another that propagates through the back. Although

using the front propagation path should be enough for TDOA esti-

mation, the back propagation path interferes with this estimation.

To counter this, a multipath interference compensation factor is

used. The resulting propagation model is presented in Eq. (8):

τ (θ ) =

sound

(θ + sin(θ )) +

sound

(sign(θ)π − 2θ)

sin(θ)

(8)

where sign(θ ) is described in Eq. (9):

sign(θ) =



−1, θ < 0

1, θ ≥ 0

(9)

In [65], an addition to the propagation model in Eq. (8) is

made to consider an attenuation factor β

(typically set to 0.1, as

suggested by the authors) as presented in Eq. (10):

τ (θ ) =

sound

(θ + sin(θ ))

sound

(sign(θ)π − 2θ)

sin(θ)

. (10)

In [44], the authors reached the same models presented in

Eqs. (2) and (7) from the point of view of auditory epipolar ge-

ometry (AEG) [23]. Epipolar geometry is popularly used in stereo

computer vision to physically localize features extracted from two

images simultaneously captured from two cameras with known

locations [79]. The revision to AEG (RAEG) made in [44] is analo-

gous to the Fourier transform of the model presented in Eq. (7). The

authors applied the following grid-search mapping to carry out 1-

D SSL: (1) using RAEG, a set of inter-microphone phase differences

(IPD

) are calculated for each possible f and DOA; (2) an



IPD

estimated from the incoming signals in the selected f ’s; and (3)

剩余26页未读，继续阅读

评论收藏

内容反馈

潮浪之巅

粉丝: 4w+
资源: 1

17J_Localization of sound sources in robotics A review_麦克风阵列声源测向...

最新资源

17J_Localization of sound sources in robotics A review_麦克风阵列声源测向...

论文研究-基于麦克风阵列和虚拟仪器的声源定位.pdf

论文研究-基于麦克风阵列的声源定位聚焦算法研究 .pdf

基于麦克风阵列的声源定位方法研究_王钊.caj

毕业设计基于麦克风阵列的声源定位技术

localization-of-sound-source.zip_localization_sound localization

ＲＯＳ定位功能包：ｒｏｂｏｔ＿ｌｏｃａｌｉｚａｔｉｏｎ

robot_localization_localization_雷达定位ekf_环境建图_ROS_ros小车建图_

使用robot_localization 实现传感器融合 的深入分步教程_设计_文档_相关文件_下载

LS_Localization_localization_最小二乘法_

论文研究-移动机器人空间声源目标定位.pdf

本科毕业设计完成版-基于matlab实现的麦克风阵列下互相关函数分类的声源定位算法研究+模型+源代码+文档说明

论文研究-用于麦克风阵列的阵元筛选方法研究 .pdf

机器人的声源定位——基于NAO机器人

分布式麦克风阵列的声源定位.docx

（matlab）GCC-PHAT方法处理线性麦克风阵列声源定位。

sound-source-localization.zip_The Program_localization_sound loc

imu_gps_localization代码注释版.zip

一种分布式双麦克风线阵声源定位方法.pdf

wifi_localization_WiFi数据集_室内定位_WiFi室内定位_

毕业设计基于matlab麦克风阵列的TDOA-SRP的声源定位功能仿真算法源码+项目说明.zip

针对头佩式麦克风阵列的声源定位算法研究

毕业设计 基于麦克风阵列的声源定位系统.zip

基于压缩感知的麦克风阵列声源定位算法

wireless localization_localization_tentvts_无线网络定位克拉美罗_定位克拉美罗_

dw.rar_sound localization_声源_声源定位_声源定位’_声音 定位

hdl_global_localization

PythonRobotics a Python code collection of robotics algorithms.pdf

最新资源

使用robot_localization 实现传感器融合的深入分步教程_设计_文档_相关文件_下载

毕业设计基于麦克风阵列的声源定位系统.zip

dw.rar_sound localization_声源_声源定位_声源定位’_声音定位