数据结构习题答案(刘小晶等主编)

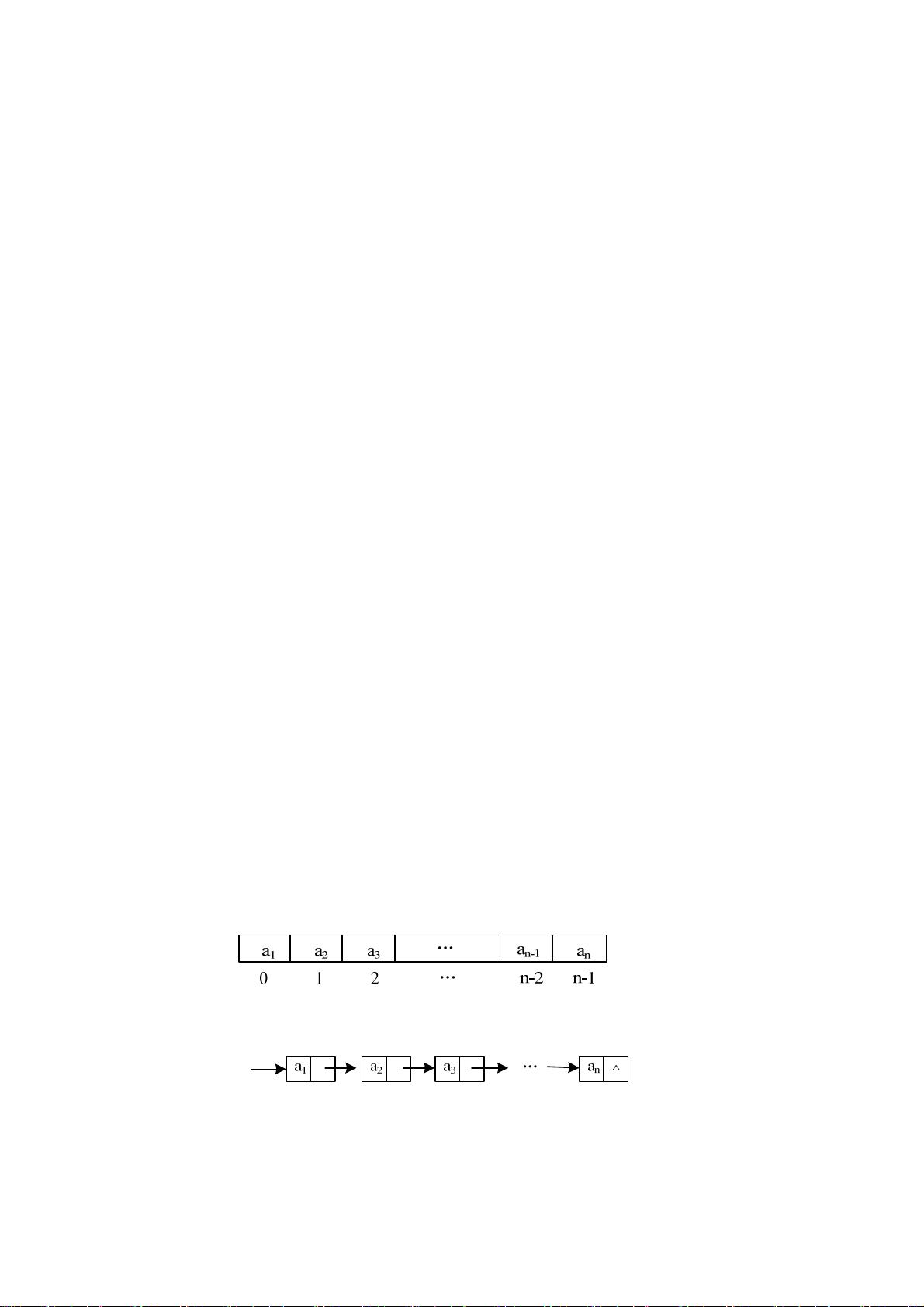
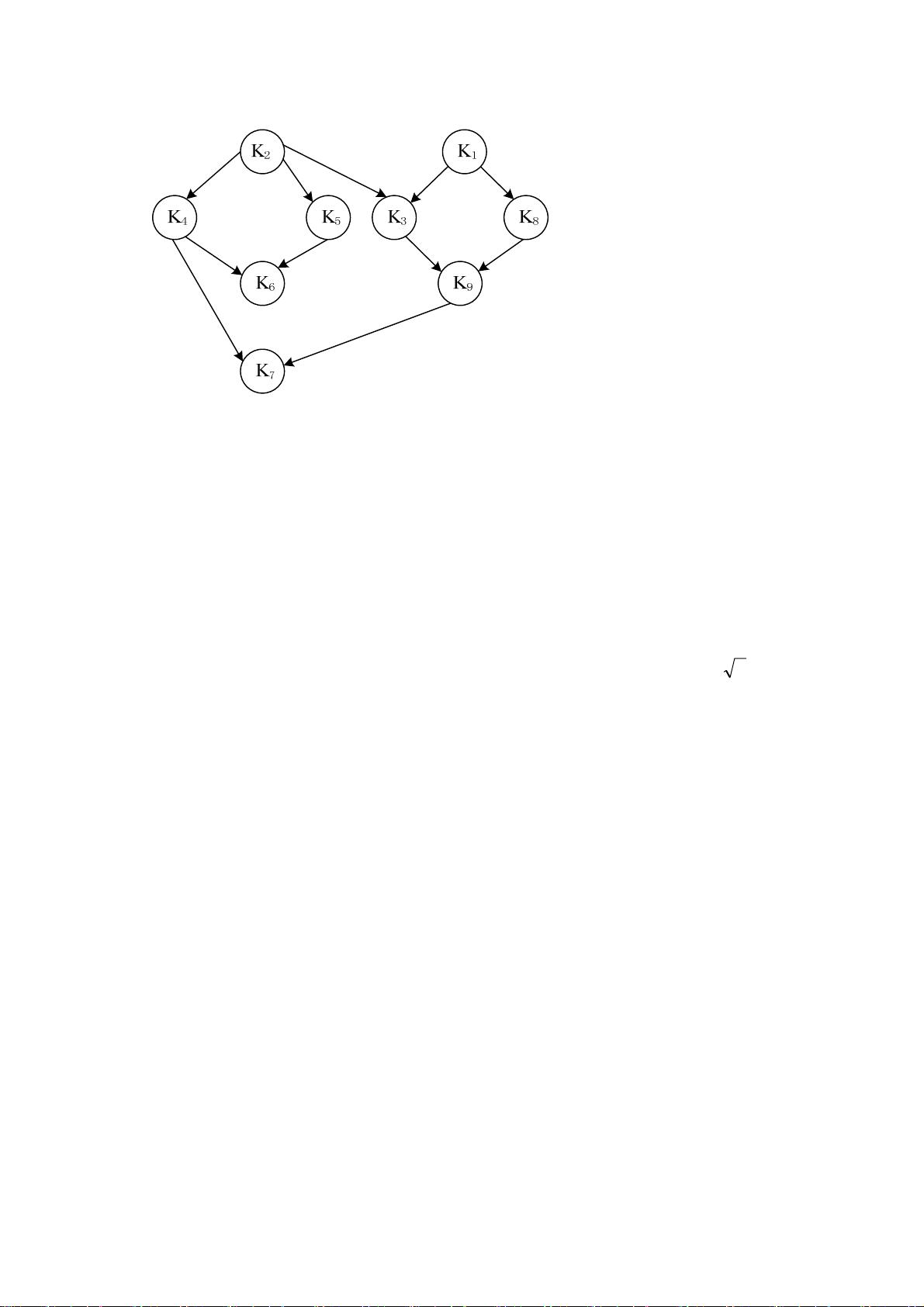
### 数据结构习题答案解析 #### 一、概念题解析 **1. 试述下列各组概念：** - **⑴数据、数据元素、数据项** - **数据**: 泛指客观事物的属性、数量、位置及其相互关系等可以被识别的符号。 - **数据元素**: 在计算机科学中，数据的基本单位，在计算机内存中通常作为一个整体进行考虑和处理。 - **数据项**: 组成数据元素的、具有独立含义的、不可分割的最小单位。 - **⑵数据结构、数据的逻辑结构、数据的存储结构** - **数据结构**: 数据组织的形式或数据之间的相互联系，它是带有结构特性的数据元素的集合。 - **数据的逻辑结构**: 数据元素之间的逻辑关系，与数据的实际存储方式无关。 - **数据的存储结构**: 数据结构在计算机中的表示方法，也称为物理结构，具体表现为数据元素在计算机中的存储方式。 - **⑶数据类型、数据操作** - **数据类型**: 数据的种类，用于定义数据的性质和类型，如整数、浮点数、字符等。 - **数据操作**: 对数据执行的操作，如插入、删除、查找等。 - **⑷算法、算法的时间复杂度、算法的空间复杂度** - **算法**: 解决特定问题的一系列明确、有限步骤的指令集。 - **算法的时间复杂度**: 描述算法运行时间与输入规模之间的增长关系。 - **算法的空间复杂度**: 描述算法运行过程中临时占用存储空间大小的变化。 **2. 试述数据结构研究的3个方面的内容。** - **数据的逻辑结构**: 定义数据元素之间的逻辑关系，例如线性结构、树形结构、图结构等。 - **数据的存储结构**: 指数据在计算机内部的存储方式，包括顺序存储结构和链式存储结构等。 - **数据的运算（操作）**: 对数据执行的具体操作，如插入、删除、查找等。 **3. 试述集合、线性结构、树型结构和图型结构四种常用数据结构的特性。** - **集合结构**: 集合中的元素之间除了属于同一个集合外没有其他关系，它们之间的关系是松散的。 - **线性结构**: 数据元素之间存在一对一的关系，如数组、链表等。 - **树形结构**: 数据元素之间存在一对多的关系，如二叉树、多叉树等。 - **图形结构**: 数据元素之间存在多对多的关系，如图结构中的顶点通过边相互连接。 **4. 设有数据的逻辑结构的二元组定义形式为B=(D,R)，其中D={a1,a2,…,an}，R={<ai,ai+1>|i=1,2,…，n-1}，请画出此逻辑结构对应的顺序存储结构和链式存储结构的示意图。** - **顺序存储结构**: 可以将数据元素依次存储在一个连续的内存区域中，如数组。 - **链式存储结构**: 每个数据元素不仅包含自身的值，还包含指向下一个数据元素的指针，形成链表。 **5. 设一个数据结构的逻辑结构如图1.9所示，请写出它的二元组定义形式。** - **二元组定义形式**: B=(D,R)，其中D为数据元素的集合，R为数据元素之间的关系集合。 **6. 设有函数f(n)=3n²-n+4，请证明f(n)=O(n²)。** - **证明**: 根据大O符号的定义，存在常数c和n₀，使得对于所有的n ≥ n₀，|f(n)| ≤ c|g(n)|。这里c=6，n₀=1，因此对于所有n≥1，0 ≤ 3n²-n+4 ≤ 6n²恒成立，满足f(n)=O(n²)的条件。 **7. 请比较下列函数的增长率，并按增长率递增的顺序排列下列函数。** - 排列顺序: 1/log₂n < 2¹⁰⁰ < log₂(log₂n) < log₂n < n^(1/2) < n^(2/3) < n < nlog₂n < n^(3/2) < nlog₂n < (4/3)^n < (3/2)^n < n! < n^n - **解释**: 增长率从小到大排序，考虑各种基本的增长函数（如对数、多项式、指数和阶乘）的增长速度差异。 **8. 试确定下列程序段中有标记符号“*”的语句行的语句频度（其中n为正整数)。** - **解析**: - **⑴i=1;k=0; while(i<=n-1)**: 语句频度为n-1。 - **⑵i=1;k=0; do{...} while(i<=n-1)**: 语句频度为n-1（当n>1时），n=1时频度为1。 - **⑶i=1;k=0; while(i<=n-1)**: 语句频度为n-1。 - **⑷k=0; for(i=1;i<=n;i++){...}**: 语句频度为n(n+1)/2。 - **⑸i=1;j=0; while(i+j<=n)**: 语句频度为n。 - **⑹x=n;y=0; while(x>=(y+1)*(y+1))**: 语句频度约为√n。 - **⑺x=91;y=100; while(y>0)**: 语句频度为1100。 - **⑻a=1;m=1; while(a<n)**: 语句频度为log₃n。 **二、算法设计题解析** **1. 有一个包括100个数据元素的数组，每个数据元素的值都是实数，试编写一个求最大数据元素的值及其下标的算法，并分析算法的时间复杂度。** - **算法代码**: ```java void findMax(double[] a) { double max = a[0]; // 初始化最大值为数组中的第一个元素 int index = 0; // 最大值的下标 for (int i = 1; i < a.length; i++) { if (max < a[i]) { max = a[i]; index = i; } } System.out.println("最大的实数为：" + max + "\n其在数组中的下标为：" + index); } ``` - **时间复杂度分析**: - 该算法的时间复杂度为O(n)，其中n为数组的长度。这是因为算法中有一个线性循环来遍历数组的所有元素，找到最大值及其下标。在这个过程中，循环体内的操作是固定的，不依赖于数组的大小，因此整体时间复杂度为O(n)。 通过以上解析，我们可以看出，数据结构课程的学习重点在于理解各种数据结构的特点以及如何有效地利用这些结构来解决问题。同时，对于算法的设计和分析也是至关重要的，这有助于我们选择合适的解决方案并评估其效率。