The Divide-and-Conquer Strategy

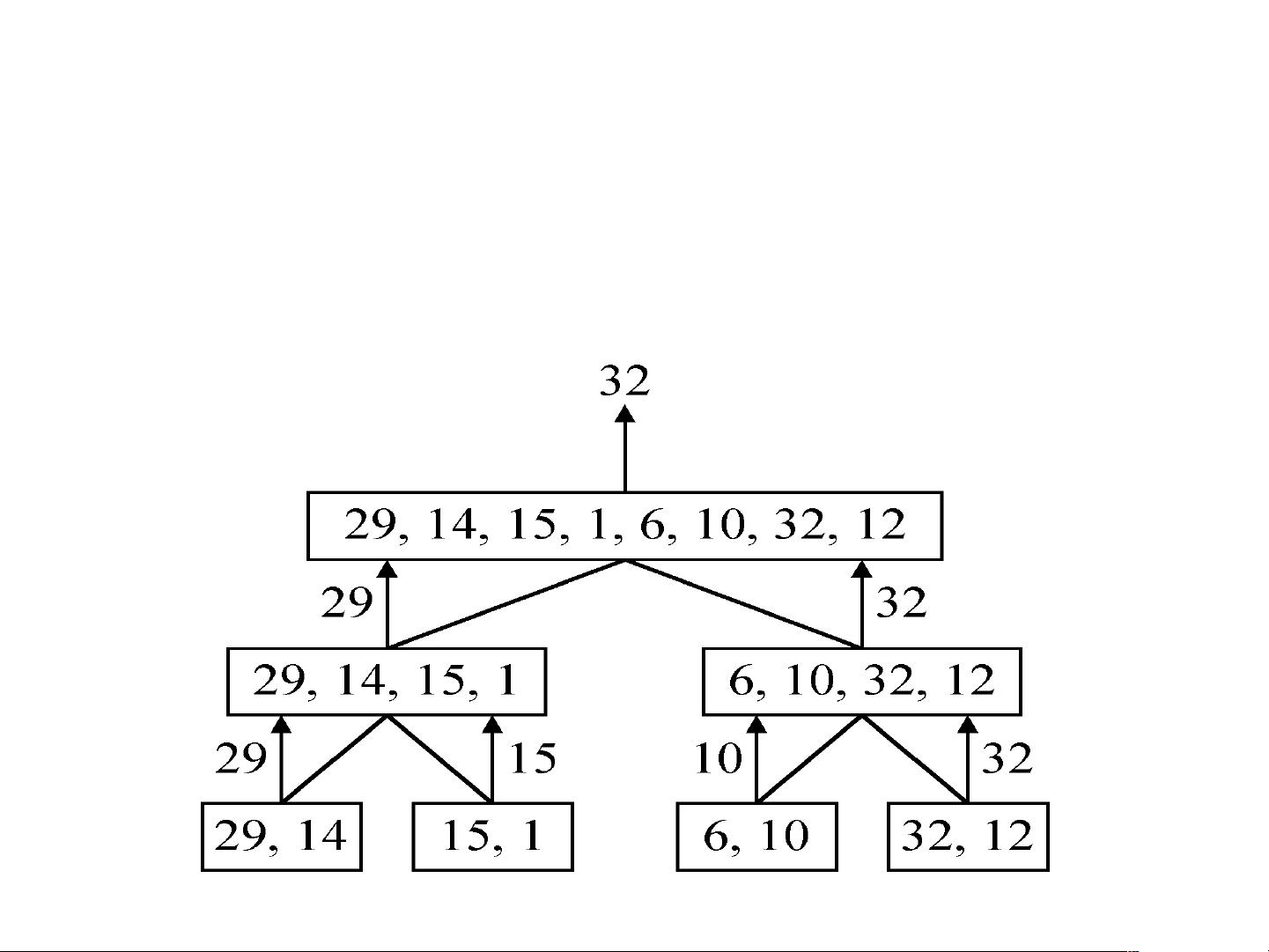
《分治策略》 分治策略是算法设计中一种重要的思想，它将一个复杂的问题分解成两个或更多的相同或相似的子问题，直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这种方法常用于解决大规模问题，能够有效地降低问题的复杂度。 以寻找一组数中的最大值为例，这是一个非常基础的分治问题。当数据量n较小，可以直接比较找出最大值。若n较大，则可以将集合S分为两半，分别递归地寻找左右两半的最大值，然后比较两者得到整体的最大值。计算时间复杂度，假设n为2的k次幂，我们可以得到递推关系式T(n) = 2T(n/2) + 1，并通过求和得出T(n) = n-1，这意味着在最坏情况下，我们需要比较n-1次来找到最大值。 一般化的分治算法包括三个步骤：判断问题规模是否小到可以直接解决；如果规模较大，将原问题分解为两个规模相等的子问题，并递归地应用算法解决；合并子问题的解以得到原问题的解。例如，二分查找、快速排序和归并排序都是分治策略的经典应用。其中，二分查找的时间复杂度为O(log n)，快速排序和归并排序的时间复杂度为O(n log n)。 2D最大值查找问题是一个更复杂的实例。在这个问题中，我们寻找那些不被其他点在X轴和Y轴上都超越的点。直接的方法是逐对比较所有点，时间复杂度为O(n^2)。然而，通过分治策略，我们可以先将点集S沿着X轴划分成两个相等大小的集合SL和SR，再分别递归地找寻这两个子集的最大值。然后，取SR集合中y坐标最大的点，去除SL中y坐标小于这个值的所有最大点。这样，整个算法的时间复杂度降为O(n log n)。 另一个与之相关的问题是最近点对问题，即给定一组n个点，找出其中距离最近的两点。这也是一种可以利用分治策略优化的复杂问题，通过空间划分和递归处理，可以有效地降低计算复杂度。 分治策略是解决问题的有效工具，尤其在处理大规模数据时，它通过分解问题、递归求解和合并结果，能显著提高算法的效率。在实际编程和算法设计中，理解和掌握分治策略对于解决复杂问题具有重要意义。