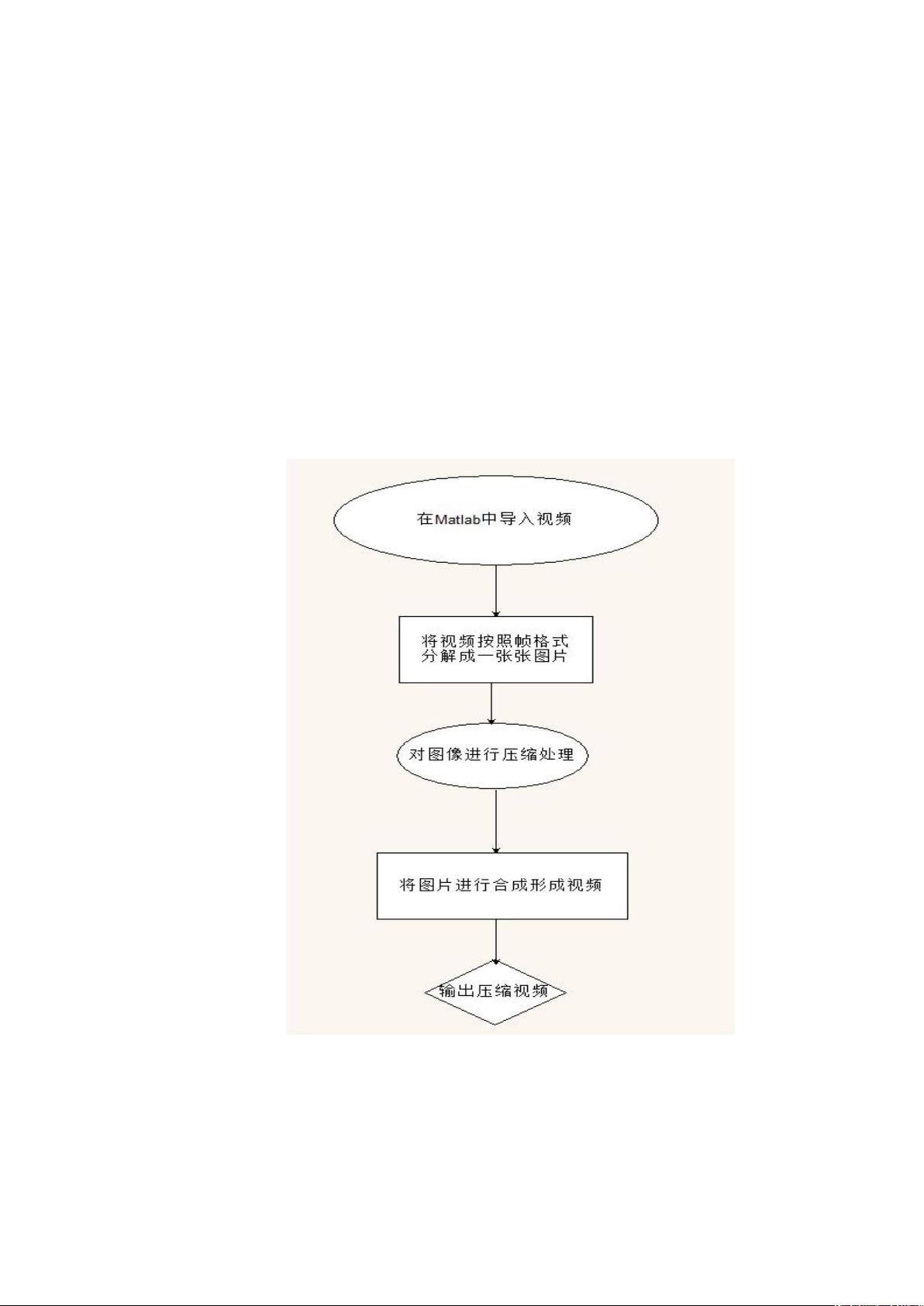
一.设计思路及框架
我们知道视频其实是由一帧一帧的图片按照一定延迟组合而成的,视频的
清晰度与容量大小取决于帧图片的分辨率以及延迟的流畅度。所以我们要对视
频进行压缩,就要对其帧图片进行压缩,也就是我们常见的图像压缩。要进行
图像压缩,首先要把视频中的帧抽取出来,在对一个个帧进行图像压缩处理,
最后将处理过的帧按照以前规律进行组合,最终形成压缩处理的视频。大体流
程图如下:
二.基于 Matlab 设计主要原理:
1.导入视频:
因为我们对于视频处理的平台是 Matlab,所以选取的视频需要符合 Matlab

标准。其中 Matlab 比较适用于导入 AVI 格式的视频,其中所用到的函数就是
[lename,pathname,leindex]=uigeile('1.avi');其中 uigeile 表示导入相应的视频
文件。同时,我们可以调用 aviinfo 函数,通过它可以知道 avi 视频的信息。在
cmd 中输入指令可以得到:
obj =
Filename: 'C:\Program
Files\MATLAB\R2010b\bin\1.avi'
FileSize: 26270720
FileModDate: '27-三月-2007 15:11:02'
NumFrames: 114
FramesPerSecond: 15
Width: 320
Height: 240
ImageType: 'truecolor'
VideoCompression: 'none'
Quality: 0
NumColormapEntries: 0
其中 NumFrames 表示视频帧数,我们选择的视频是 114 帧。我选择的是
Matlab 自带的 AVI 视频,选择它主要因为一下几点。第一,它是 Matlab 自带的,
兼容性好,不会出现导入错误的情况。第二,它时长很短,只有 8 秒,所以产
生的图片帧不多,只有 114 帧,因此在进行图片处理的时候比较方便。第三,
它虽然比较短,但它仍然有 25M 的容量,因此在压缩时变化还是比较明显,方
便我们观察。
2.视频成帧
因为视频是由一个个帧组成的,所以任何一个视频都可以分解成一个个帧 。
在 Matlab 上,借由它本身的函数,我们可以很容易地对它进行拆分,主要采用
了先前 aviinfo 函数,获取了 AVI 视频的大量信息,包括帧。然后通过 imwrite 函
数对这些帧进行输出。因为有 114 帧,所以采用 for 循环,从 1 到 114 一次进行

输出。具体代码如下:
len=obj.NumFrames;
for k=1:len
readerobj(k)=aviread(obj.Filename,k); %¶ÁÈëaviÎļþµÄµÚkÖ¡
image=readerobj(k).cdata;
imwrite(image,strcat(int2str(k),'.bmp'),'bmp');
end
3.图片压缩技术
几大主要图像压缩算法
(1)傅里叶变化:
傅里叶变换是线性系统分析的一个有力工具,它将图像从空域变换到
频域,从而很容易地了解到图像各空间频域成分,从而进行相应的处理。傅里
叶变换应用十分广泛,如图像特征提取、空间频率域滤波、图像恢复、纹理分
析等。ä
如果一个周期为 T 的函数在[-T/2,T/2]上满足狄利克雷条件,则函数在[-T/2,T/2]上
可以展开成傅里叶级数。ä
可见,傅里叶级数清楚地表明了一个周期信号由哪些频率分量组成及其所占的
比重,从而有利于对周期信号进行分析和处理。ä
根据周期信号的这个特点,可以把傅里叶级数的概念推广到非周期信号上,这
就引出了傅里叶变换。
(2)离散余弦变换的原理
离散余弦变换(DCT for Discrete Cosine Transform)是与傅里叶变换相关的一种
变换,它类似于离散傅里叶变换(DFT for Discrete Fourier Transform),但是只使用
实数。离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换,这个离
散傅里叶变换是对一个实偶函数进行的(因为一个实偶函数的傅里叶变换仍然是

一个实偶函数),在有些变形里面需要将输入或者输出的位置移动半个单位(DCT
有 8 种标准类型,其中 4 种是常见的)。ääää最常用的一种离散余弦变换的类型是
下面给出的第二种类型,通常我们所说的离散余弦变换指的就是这种。它的逆,
也就是下面给出的第三种类型,通常相应的被称为"反离散余弦变换","逆离散
余弦变换"或者"IDCT"。ä
有两个相关的变换,一个是离散正弦变换(DST for Discrete Sine Transform),它
相当于一个长度大概是它两倍的实奇函数的离散傅里叶变换;另一个是改进的
离散余弦变换(MDCT for Modied Discrete Cosine Transform),它相当于对交叠的数
据进行离散余弦变换。ä
这一技术可以应用到彩色图像上。彩色图像有像素组成,这些像素具有
RGB 彩色值。每个像素都带有 x,y 坐标,对每种原色使用 8x8 或者 16x16 矩阵。
在灰度图像中像素具有灰度值,它的 x,y 坐标由灰色的幅度组成。为了在 JPEG
中压缩灰度图像,每个像素被翻译为亮度或灰度值。为了压缩 RGB 彩色图像,
这项工作必须进行三遍,因为 JPEG 分别得处理每个颜色成分,R 成分第一个被
压缩,然后是 G 成分,最后是 B 成分。而一个 8x8 矩阵的 64 个值,每个值都带
有各自的 x,y 坐标,这样我们就有了一个像素的三维表示法,称作控件表达式
或空间域。通过 DCT 变换,空间表达式就转化为频谱表达式或频率域。从而到
达了数据压缩的目的。ä
DCT 式目前最佳的图像变换,它有很多优点。DCT 是正交变换,它可以将
8x8 图像空间表达式转换为频率域,只需要用少量的数据点表示图像;DCT 产生
的系数很容易被量化,因此能获得好的块压缩;DCT 算法的性能很好,它有快
速算法,如采用快速傅立叶变换可以进行高效的运算,因此它在硬件和软件中
都容易实现;而且 DCT 算法是对称的,所以利用逆 DCT 算法可以用来解压缩图
像。ä为什么采用 8x8 的图像块,其原因是由于计算量和像素之间关系的数量,
许多研究表明,在 15 或 20 个像素之后,像素间的相关性开始下降。就是说,
一列相似的像素通常会持续 15 到 20 个像素那么长,在此之后,像素就会改变
幅度水平(或反向)。ä
模拟图像经采样后成为离散化的亮度值然后分成一个个宏块,而一个宏块有分
成 8x8 大小的块,可以用一个矩阵来表示这个块。
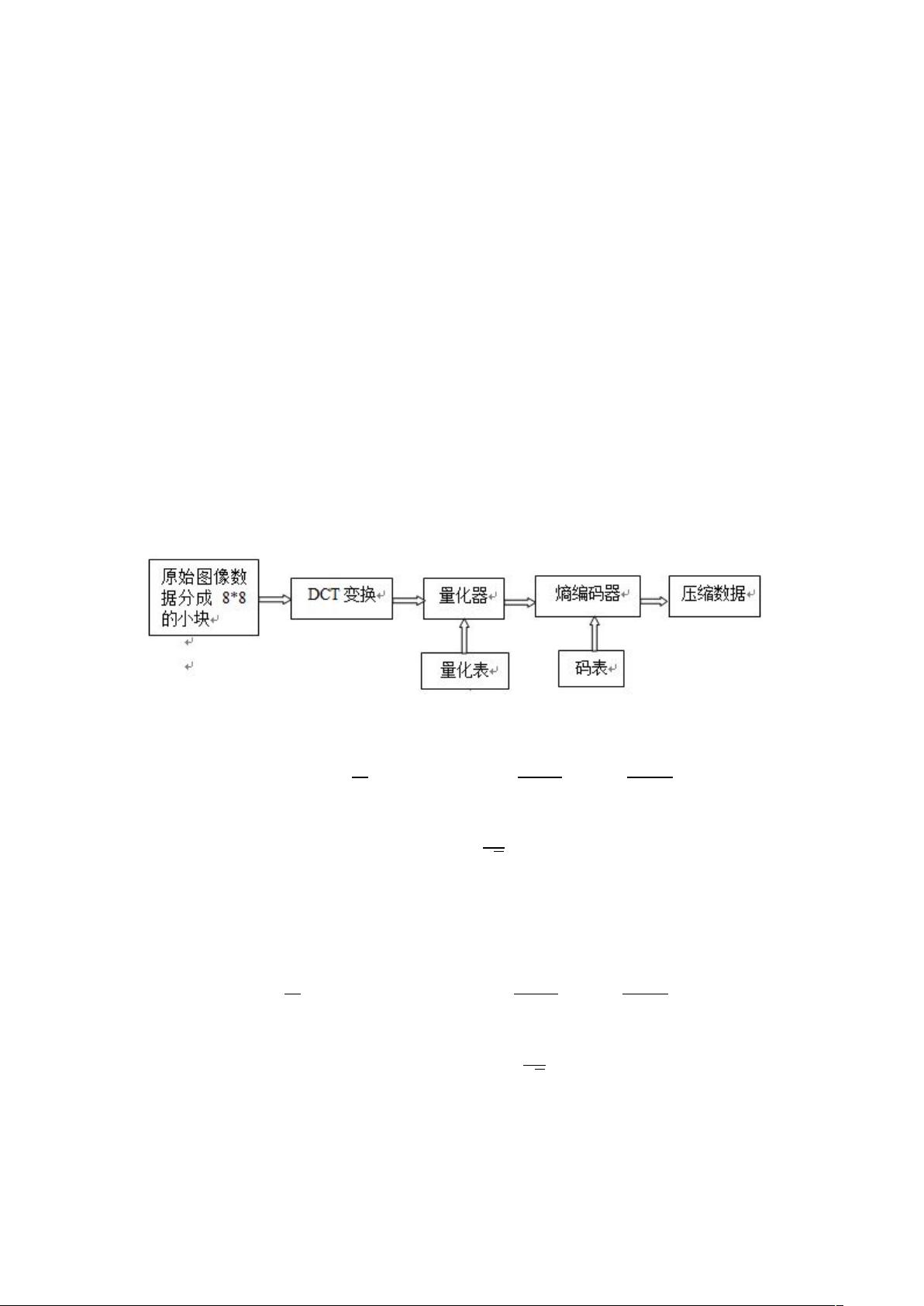
基于 DCT 的 JPEG 图像压缩编码理论算法ä基于 DCT 编码的 JPEG 编码压缩过
程框图,如图所示:
二维离散余弦正变换公式为
F
(
u , v
)
=c
(
u
)
c
(
v
)
2
N
∑
x =0
N−1
∑
y=0
N−1
f
(
x , y
)
cos
(
2 x+1
2 N
uπ
)
cos
(
2 y +1
2 N
vπ
)
x , y ,u , v=0,1 ,⋯, N−1
。
c (u)=c (v )=
{
1
√
2
u=0 , v=0
1 其它
二维离散余弦逆变换公式为
f
(
x , y
)
=
2
N
∑
u=0
N −1
∑
v =0
N−1
c
(
u
)
c
(
v
)
F
(
u , v
)
cos
(
2 x+1
2 N
uπ
)
cos
(
2 y +1
2 N
vπ
)
x , y ,u , v=0,1 ,⋯, N−1
。
c (u)=c (v )=
{
1
√
2
u=0 , v=0
1 其它
ä
JPEG 采用的是 8×8 大小的子块的二维离散余弦变换。在编码器的输入端,把原

















