数学模型第三版答案(详细版)
根据给定文件的信息,我们可以提炼出以下几个主要的知识点: ### 数学模型中委员会席位分配的方法 #### 1. 按比例分配方法 - **原理**:首先根据每个宿舍人数占总人数的比例来初步分配席位,剩余的小数部分按照大小顺序依次给予额外的席位。 - **应用**:假设学校共有1000名学生,分别住在A、B、C三个宿舍,人数分别为235、333和432人。若需要选举10人组成委员会,则首先按比例分配席位。 - **计算公式**: \[ p_i = \frac{人口_i}{总人口}, q_i = \left\lfloor p_i \times N \right\rfloor + \text{小数部分排序后的排名} \] 其中,\(N\)表示委员会席位总数;\(\left\lfloor x \right\rfloor\)表示向下取整。 - **具体步骤**: - 计算每个宿舍所占的比例:\(p_1 = 0.235, p_2 = 0.333, p_3 = 0.432\) - 计算初步分配的席位数:\(n_1 = 2, n_2 = 3, n_3 = 4\) - 将剩余的小数部分按大小排序,并依次分配剩余的席位:最终结果为A宿舍2席、B宿舍3席、C宿舍5席。 #### 2. Q值方法 - **原理**:类似于按比例分配方法,但最后一席位的分配基于“Q值”进行决定。Q值计算公式为:\(Q_i = \frac{人口_i}{(席位_i + 1)}\),其中\(席位_i\)为该宿舍已分配的席位数。 - **具体步骤**: - 前9个席位的分配与按比例分配方法相同。 - 第10个席位通过比较各宿舍的Q值确定归属。在此案例中,C宿舍的Q值最大,因此第10个席位分配给C宿舍。 #### 3. d'Hondt方法 - **原理**:采用逐步降低标准的方式分配席位。首先计算每个宿舍人数除以1至当前分配席位数的序列,然后选取商最大的前\(N\)个数值对应的宿舍分配席位。 - **具体步骤**: - 计算每个宿舍人数除以1至当前分配席位数的序列。 - 选取最大的10个数值,对应的宿舍即为分配席位的宿舍。 - 最终结果与Q值方法相同,即A宿舍2席、B宿舍3席、C宿舍5席。 ### 数学建模实例分析 #### 1. 录像带记数器读数与时间的关系 - **问题描述**:建立录像带记数器读数\(n\)与转过时间\(t\)的数学模型。 - **解决思路**:根据题目条件,可以设定录像带转过的长度与时间的关系,并利用微积分求解。 - **数学模型**: - 设录像带记数器读数为\(n\)时,录像带转过时间为\(t\)。 - 考虑\(t\)到\(t+\Delta t\)时间内录像带缠绕在右轮盘上的长度,得出\(d(n)=2\pi k(r+wn)d(t)\),其中\(k\)、\(r\)、\(w\)均为常数。 - 对上式两边进行积分,得出\(n\)与\(t\)之间的关系式。 - 结果为\(n = \sqrt{\frac{v^2t^2}{\pi^2} + \frac{k^2r^2}{w^2}} - \frac{kr}{w}\)。 #### 2. 风车获得功率与参数的关系 - **问题描述**:确定风车获得的功率\(P\)与速度\(v\)、迎风面积\(S\)、空气密度\(\rho\)的关系。 - **解决思路**:利用量纲分析法,通过量纲的一致性推导出未知量之间的函数关系。 - **数学模型**: - 设\(P = f(v, S, \rho)\)。 - 通过量纲分析,得出\(P\)与\(v\)、\(S\)、\(\rho\)之间的确切函数形式为\(P = C\rho Sv^3\),其中\(C\)为无量纲常数。 #### 3. 雨滴速度与参数的关系 - **问题描述**:给出雨滴速度\(v\)与空气密度\(\rho\)、粘滞系数\(\mu\)和重力加速度\(g\)之间的关系。 - **解决思路**:同样采用量纲分析法。 - **数学模型**: - 设\(v = f(\rho, \mu, g)\)。 - 通过量纲分析,得出\(v\)与\(\rho\)、\(\mu\)、\(g\)之间的确切函数形式为\(v = C\sqrt{\frac{g}{\mu/\rho}}\),其中\(C\)为无量纲常数。



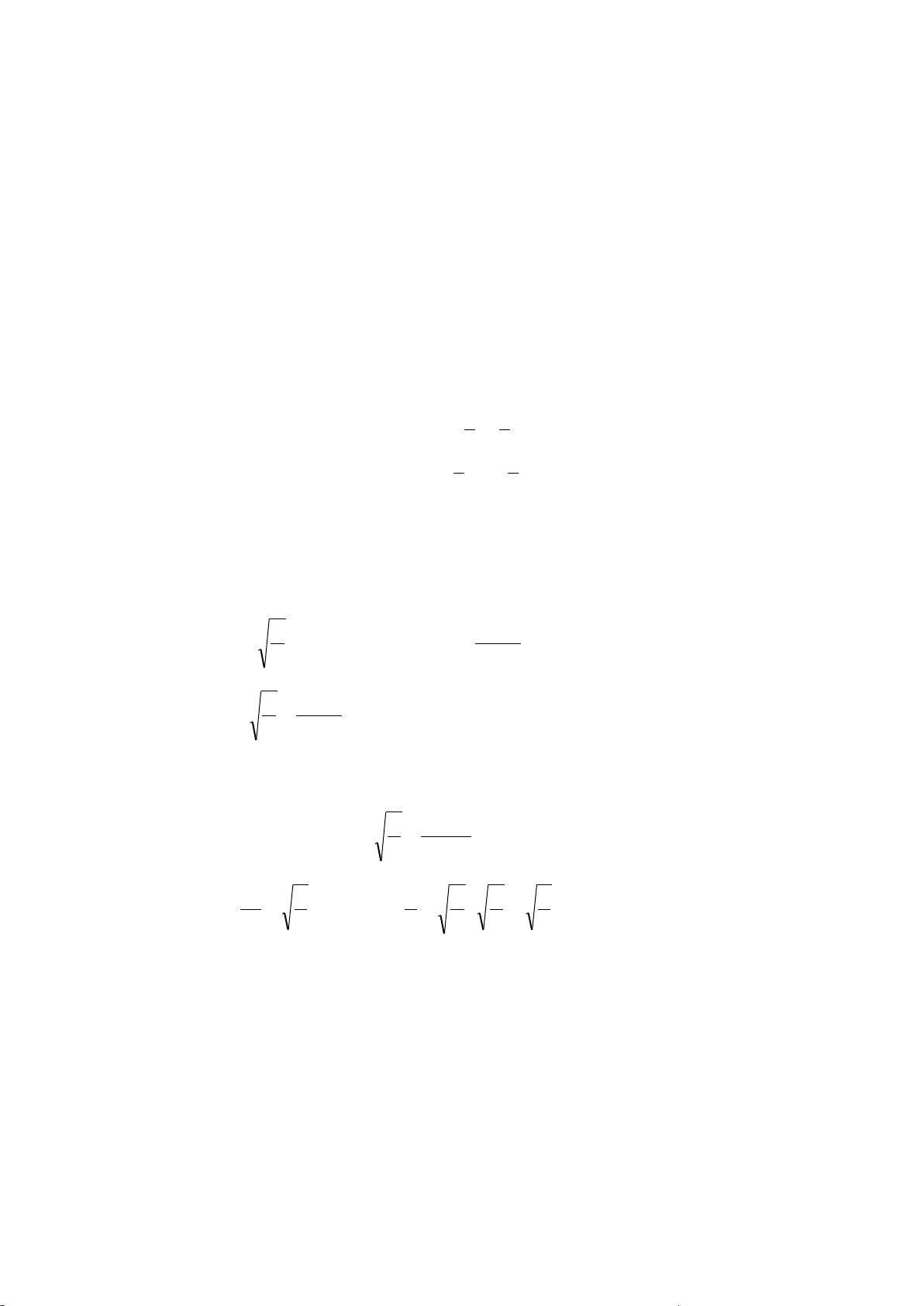
剩余57页未读,继续阅读

 yyxjy19922013-10-11非常好用!
yyxjy19922013-10-11非常好用! fayekia2012-11-14不是想要的。。不是某个教材的配套答案。。应该是某个作业题吧。。
fayekia2012-11-14不是想要的。。不是某个教材的配套答案。。应该是某个作业题吧。。
- 粉丝: 0
- 资源: 2
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- 动手学深度学习,沐神版配套代码,所有代码均可在jupyter中运行,内附有极为详尽的代码注释
- qaxbrowser-1.1.32574.52.exe (奇安信浏览器windows安装包)
- C#编写modbus tcp客户端读取modbus tcp服务器数据
- 某房地产瑞六补环境部分代码
- 基于Matlab实现无刷直流电机仿真(模型+说明文档).rar
- AllSort(直接插入排序,希尔排序,选择排序,堆排序,冒泡排序,快速排序,归并排序)
- 模拟qsort,改造冒泡排序使其能排序任意数据类型,即日常练习
- carsim+simulink联合仿真实现变道 包含路径规划算法+mpc轨迹跟踪算法 可选simulink版本和c++版本算法 可以适用于弯道道路,弯道车道保持,弯道变道 carsim内规划轨迹可视化
- 数组经典习题之顺序排序和二分查找和冒泡排序
- 永磁同步电机神经网络自抗扰控制,附带编程涉及到的公式文档,方便理解,模型顺利运行,效果好,位置电流双闭环采用二阶自抗扰控制,永磁同步电机三闭环控制,神经网络控制,自抗扰中状态扩张观测器与神经网络结合


 信息提交成功
信息提交成功