小波变换教程

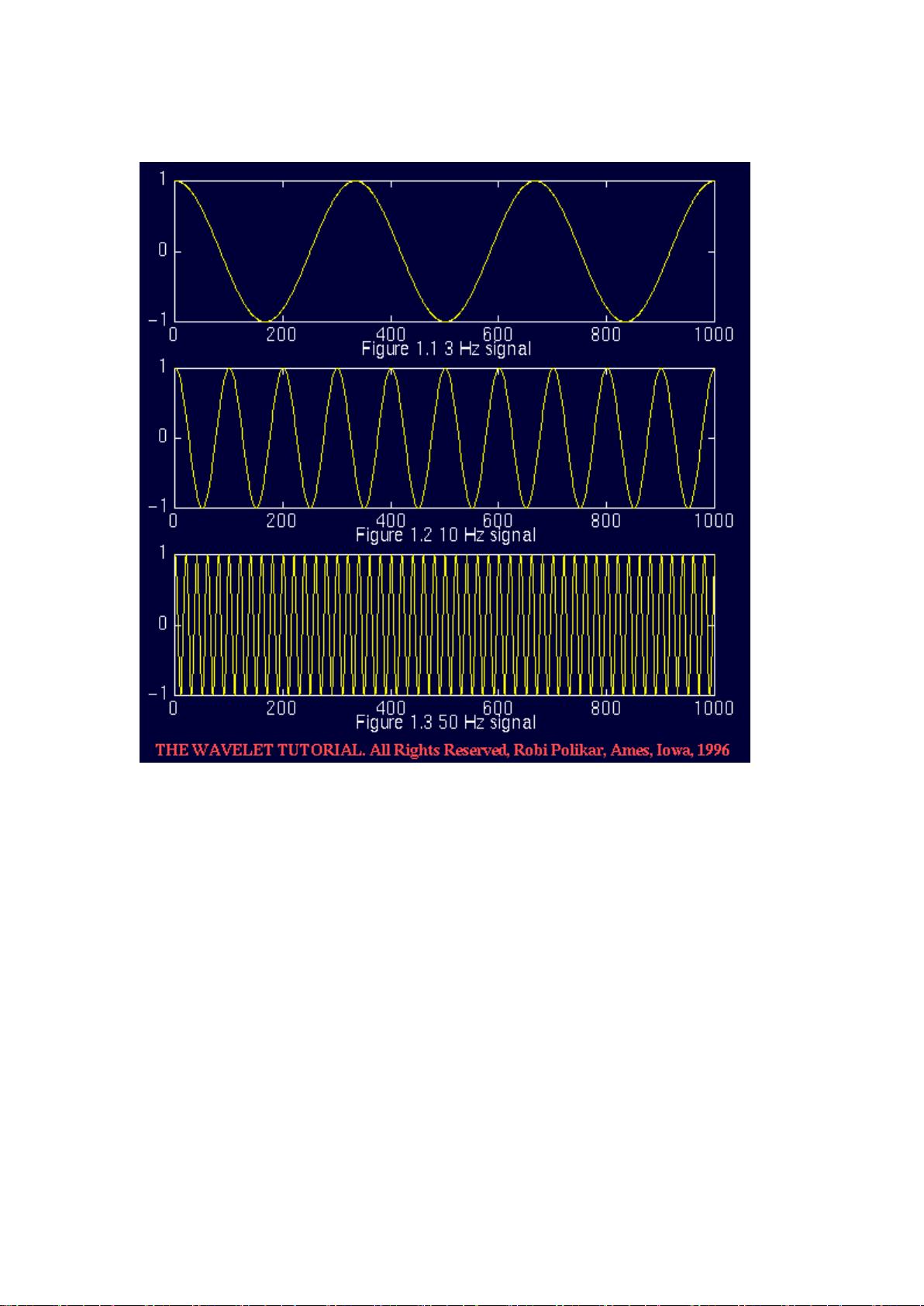
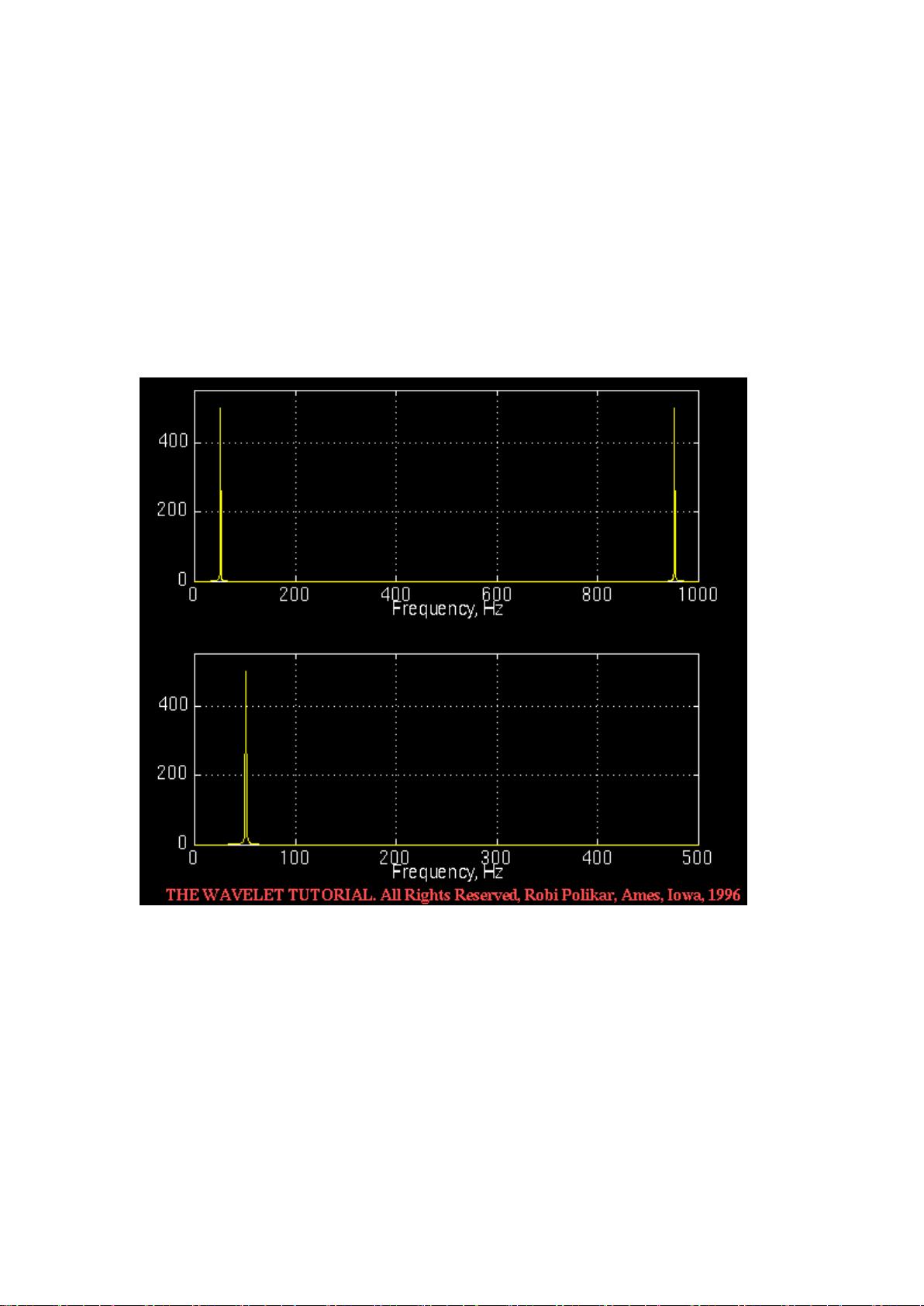
小波变换教程的知识点 小波变换是一种数学变换技术，主要用于信号处理领域。该技术与传统变换方法如傅立叶变换存在较大差异，其在时频两域上都具有良好的局部化特性，这使得它能够分析非平稳信号。以下为小波变换的主要知识点： 1. 小波变换原理 小波变换的原理是将一个函数或信号分解成一系列的小波函数的叠加。这些小波函数都是由一个母小波函数通过平移和缩放获得的。小波变换的目的是提取信号的局部特征，使得对信号的时间和频率特征可以同时获得很好的分辨率。 2. 连续小波变换（CWT） 连续小波变换是小波变换的一种形式，它通过连续变化的尺度因子和平移因子对信号进行分析。它能提供关于信号的局部时频特性，适用于对信号进行精细的时频分析。 3. 离散小波变换（DWT） 离散小波变换是对连续小波变换进行采样而得，它以离散的方式对信号进行分析。由于其计算效率高，常用于数据压缩和信号去噪等领域。 4. 二进制小波变换（也称为多分辨率分析） 二进制小波变换是一种特殊的离散小波变换，它通过二进制尺度因子和平移因子对信号进行分析。二进制小波变换与滤波器组紧密相关，常用于图像处理和特征提取。 5. 小波变换与傅立叶变换的比较 虽然傅立叶变换是分析信号频率的有效方法，但它在处理非平稳信号时存在局限性。小波变换的出现，弥补了这一不足，使得我们可以在不同的尺度上分析信号的时频特性。 6. 小波变换的应用 小波变换在信号处理领域有着广泛的应用。比如，它可以用于信号去噪、数据压缩、信号特征提取、图像处理等领域。在医学领域，小波变换可以用来分析心电图等生物信号，帮助医生更好地诊断病情。 7. 小波变换的数学基础 小波变换涉及到的数学知识包括傅立叶变换、积分变换、线性代数等。掌握这些数学知识，对于理解小波变换的原理和应用有着至关重要的作用。 小波变换是现代信号处理技术中一个非常重要的工具。它不仅能对信号进行更细致的分析，还为科研人员和工程师提供了一种新的视角来处理复杂信号。由于其良好的局部化特性，小波变换已经成为非线性和非平稳信号分析的重要方法。 小波变换教程的编写者是一位初学者，他撰写这篇教程的目的是为了让更多的初学者可以理解和应用小波变换。虽然小波变换在数学上有着复杂的理论基础，但在工程应用中，并不一定需要了解所有的理论细节。因此，教程主要关注小波变换的基本原理和应用，而未涉及深入的理论证明。如果读者对某些理论细节感兴趣，可以进一步参考文献或书籍进行学习。