spartan 3E starter kit FPGA开发板 实验二

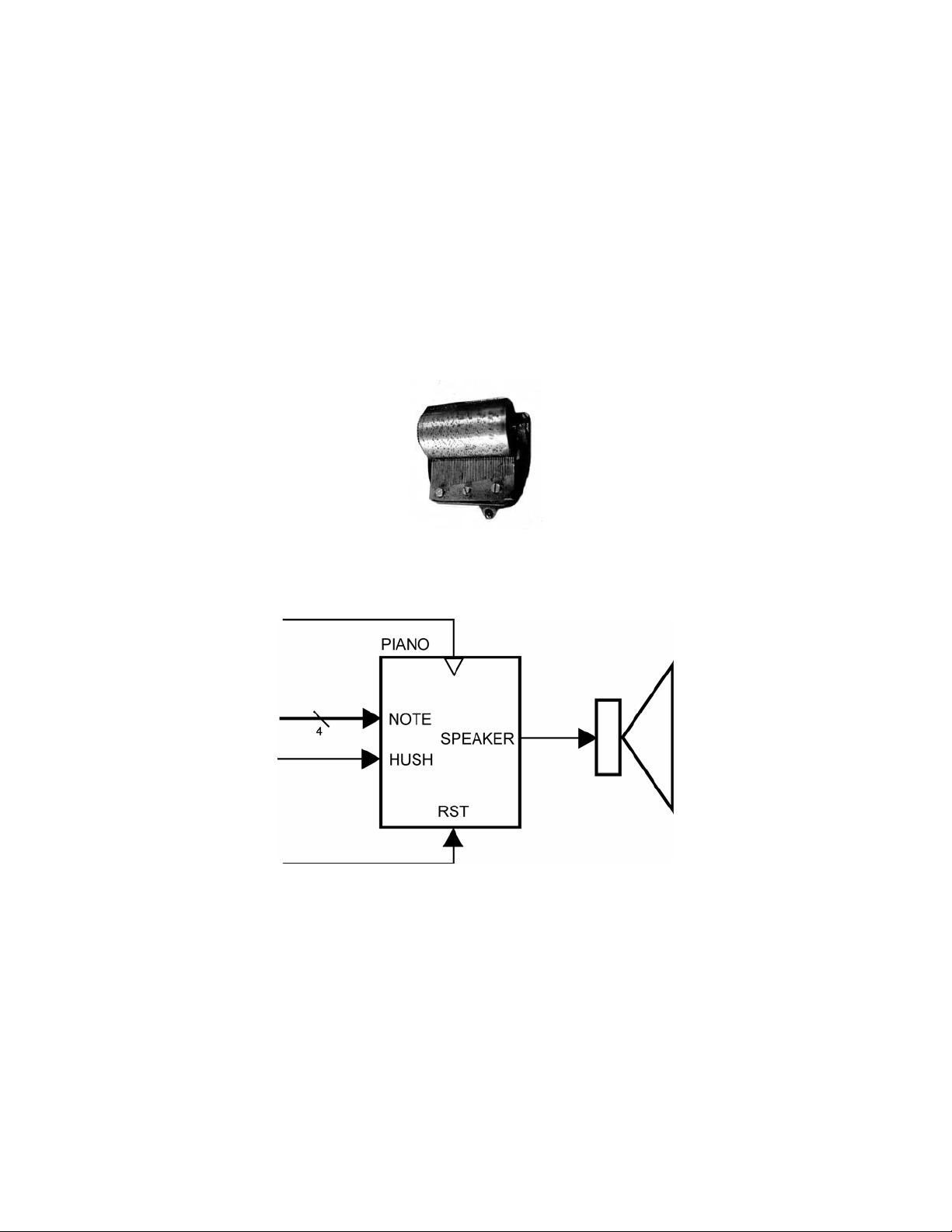
### Spartan 3E Starter Kit FPGA开发板实验二：基于用户输入生成特定频率的方波 #### 实验背景与目标 本实验是针对San Jose State University电气工程系EE178课程设计的一个实验室作业，旨在通过Spartan 3E Starter Kit FPGA开发板，帮助学生深入理解数字逻辑设计的基础概念，并通过实际操作掌握简单的逻辑电路设计方法。学生在完成实验后，将能够设计并实现一个基于用户输入信号来产生特定频率方波的电路模块。 #### 实验目的 1. **熟悉基本构建单元**：通过实验加深对触发器（flip-flops）、计数器（counters）和多路选择器（multiplexers）等基本数字逻辑组件的理解。 2. **实现特定功能的电路**：设计并实现一个能够根据用户输入信号产生不同频率方波的电路。 3. **知识产权积累**：通过本实验所设计的电路可以作为未来的知识产权，为后续更复杂的设计提供基础模块。 #### 实验模块描述与需求 - **不允许使用的组件**：设计中不得使用锁存器（latches）。 - **时钟与复位信号**：仅允许使用一块时钟和一个异步复位信号。时钟信号必须是来自开发板振荡器提供的50MHz时钟信号。 - **输入信号**： - `clk`：50MHz时钟信号。 - `rst`：复位信号。 - `note[3:0]`：四比特输入用于选择16种不同的音调。 - `hush`：停止音频输出信号，使输出静音。 - **输出信号**： - `speaker`：音频输出信号，用于驱动扬声器输出特定频率的方波。 - **模块行为要求**： - 当`hush`信号有效低时，输出的方波应该停止翻转，但输出值不变。 - 复位信号`rst`不仅能禁止输出信号的翻转，还能将输出信号强制回到一个已知的初始状态。 - 根据`note[3:0]`输入的不同值，输出特定频率的方波。 #### 设计过程 1. **确定频率范围**：首先需要确定用户可选的16种音调对应的频率范围，这需要根据具体的音乐理论和音高标准进行计算。 2. **设计频率控制逻辑**：基于选定的频率范围，设计一个逻辑电路，该电路能够根据`note[3:0]`的输入值输出对应频率的方波。 3. **实现复位逻辑**：设计一个复位逻辑电路，当复位信号`rst`有效时，该电路能够使输出信号`speaker`返回到一个已知的状态，并停止方波的翻转。 4. **实现静音逻辑**：设计一个静音逻辑电路，当`hush`信号有效时，该电路能够禁止方波的翻转，但保持输出值不变。 5. **综合与测试**：利用FPGA开发软件完成电路的综合与布局布线，并通过模拟测试验证电路的功能是否符合预期。 6. **调试与优化**：根据测试结果对设计进行必要的调整和优化，确保电路的稳定性和可靠性。 通过以上步骤，学生不仅能够深入了解数字逻辑设计的基本原理和技术，还能够在实践中锻炼自己的逻辑思维能力和问题解决能力，为将来从事更复杂的电子系统设计打下坚实的基础。