h
(0)
A
h
(3)
h
(1)
A
B
h
(2)
B
C
C
h
(3)
C
h
(0)
h
(2)
B
B
h
(1)
A
A
C
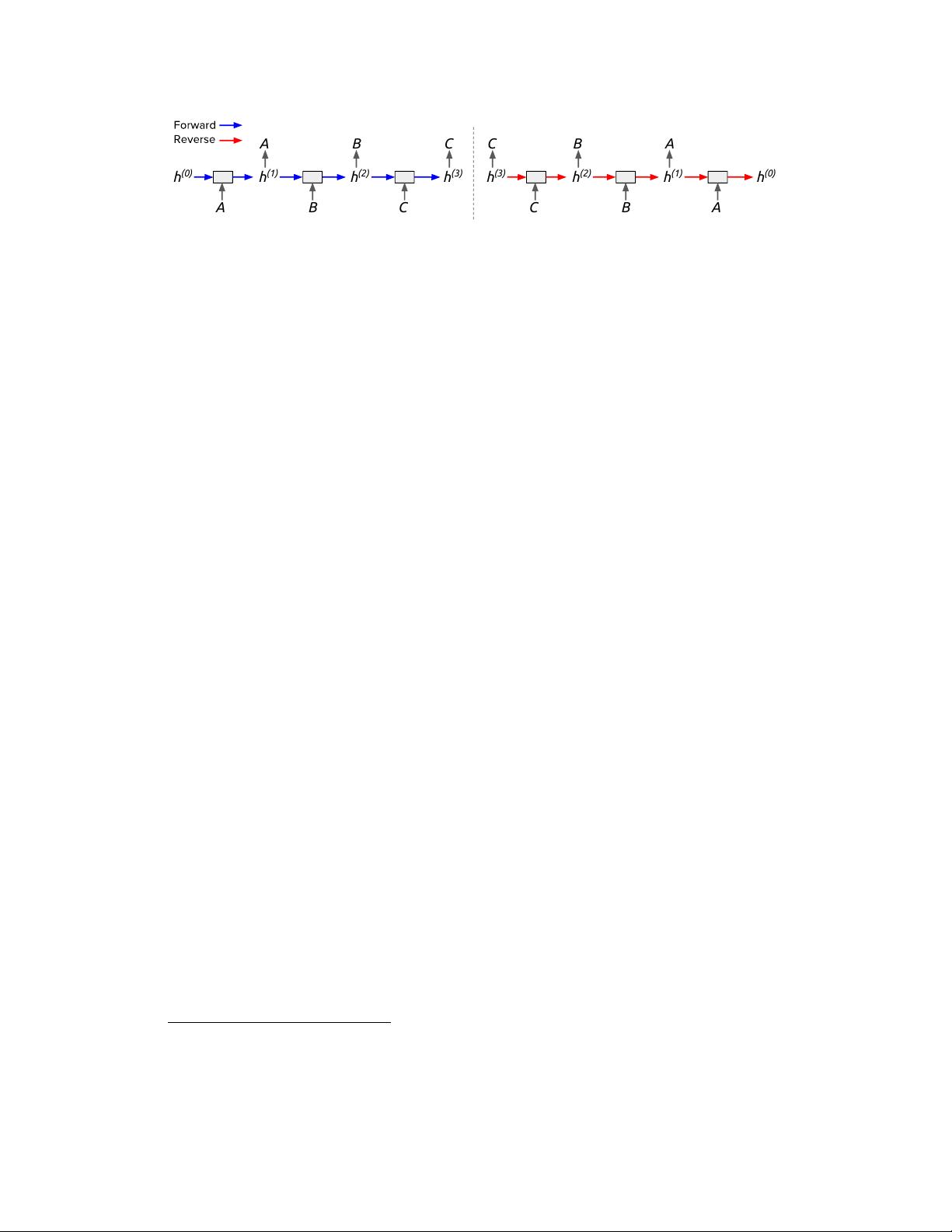
Figure 1: Unrolling the reverse computation of an exactly reversible model on the repeat task yields a sequence-
to-sequence computation.
Left:
The repeat task itself, where the model repeats each input token.
Right:
Unrolling the reversal. The model effectively uses the final hidden state to reconstruct all input tokens, implying
that the entire input sequence must be stored in the final hidden state.
4 Impossibility of No Forgetting
We have shown reversible RNNs in finite precision can be constructed by ensuring that no information
is discarded. We were unable to find such an architecture that achieved acceptable performance on
tasks such as language modeling
3
. This is consistent with prior work which found forgetting to be
crucial to LSTM performance [
23
,
24
]. In this section, we argue that this results from a fundamental
limitation of no-forgetting reversible models: if none of the hidden state can be forgotten, then the
hidden state at any given timestep must contain enough information to reconstruct all previous hidden
states. Thus, any information stored in the hidden state at one timestep must remain present at all
future timesteps to ensure exact reconstruction, overwhelming the storage capacity of the model.
We make this intuition concrete by considering an elementary sequence learning task, the repeat task.
In this task, an RNN is given a sequence of discrete tokens and must simply repeat each token at the
subsequent timestep. This task is trivially solvable by ordinary RNN models with only a handful of
hidden units, since it doesn’t require modeling long-distance dependencies. But consider how an
exactly reversible model would perform the repeat task. Unrolling the reverse computation, as shown
in Figure 1, reveals a sequence-to-sequence computation in which the encoder and decoder weights
are tied. The encoder takes in the tokens and produces a final hidden state. The decoder uses this
final hidden state to produce the input sequence in reverse sequential order.
Notice the relationship to another sequence learning task, the memorization task, used as part of
a curriculum learning strategy by Zaremba and Sutskever
[25]
. After an RNN observes an entire
sequence of input tokens, it is required to output the input sequence in reverse order. As shown in
Figure 1, the memorization task for an ordinary RNN reduces to the repeat task for an NF-RevRNN.
Hence, if the memorization task requires a hidden representation size that grows with the sequence
length, then so does the repeat task for NF-RevRNNs.
We confirmed experimentally that NF-RevGRU and NF-RevLSM networks with limited capacity
were unable to solve the repeat task
4
. Interestingly, the NF-RevGRU was able to memorize input
sequences using considerably fewer hidden units than the ordinary GRU or LSTM, suggesting it may
be a useful architecture for tasks requiring memorization. Consistent with the results on the repeat
task, the NF-RevGRU and NF-RevLSTM were unable to match the performance of even vanilla
RNNs on word-level language modeling on the Penn TreeBank dataset [14].
5 Reversibility with Forgetting
The impossibility of zero forgetting leads us to explore the second possibility to achieve reversibility:
storing information lost from the hidden state during the forward computation, then restoring it in the
reverse computation. Initially, we investigated discrete forgetting, in which only an integral number
of bits are allowed to be forgotten. This leads to a simple implementation: if
n
bits are forgotten in
the forwards pass, we can store these
n
bits on a stack, to be popped off and restored to the hidden
state during reconstruction. However, restricting our model to forget only an integral number of
bits led to a substantial drop in performance compared to baseline models
5
. For the remainder of
3
We discuss our failed attempts in Appendix A.
4
We include full results and details in Appendix B. The argument presented applies to idealized RNNs able
to implement any hidden-to-hidden transition and whose hidden units can store 32 bits each. We chose to use
the LSTM and the NF-RevGRU as approximations to these idealized models since they performed best at their
respective tasks.
5
Algorithmic details and experimental results for discrete forgetting are given in Appendix D.
4






 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功