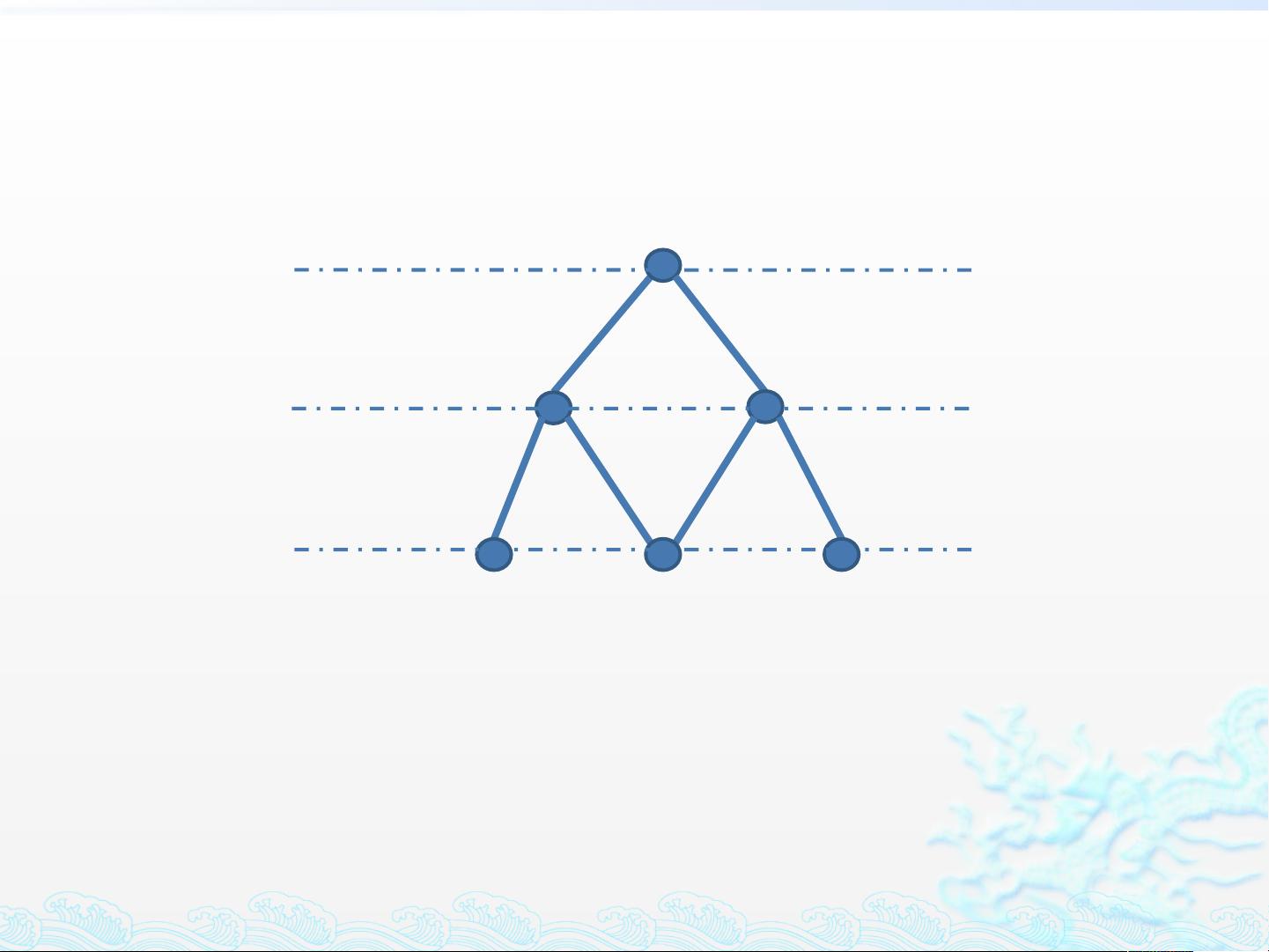
### 程序设计方法——动态规划法
#### 动态规划法介绍
动态规划（Dynamic Programming，简称DP）是一种在计算机科学与数学优化中用来解决问题的方法，它通过把原问题分解成相对简单的子问题的方式来求解。尤其适用于具有重叠子问题和最优子结构特征的问题。
#### 摘桃子问题
摘桃子问题是一个典型的动态规划问题，可以通过自底向上的方法求解。题目描述如下：
- **问题背景**：有一棵桃树，树的形状呈现为一个三角形，每层树枝数量等于该层编号（第1层有1条树枝，第2层有2条树枝，以此类推）。每条树枝上标有一个数字，代表该树枝最多可以摘取的桃子数量。
- **游戏规则**：小猴子从最低层开始向上爬，每次只能选择向左或向右的树枝爬行，并尽可能地摘取更多的桃子，直到到达树顶。
- **目标**：求出从小猴子所在的最低层到树顶的最大桃子数。
#### 解题思路
本题的关键在于如何确定最优策略，即每次选择哪条路径可以获得最大的收益（桃子数量）。
1. **递归回溯方法**：首先可以考虑使用递归回溯的方法来解决问题，即从树顶向下遍历，尝试每一种可能的路径，记录每条路径的总桃子数，最终选取桃子数最多的那条路径。但是这种方法的时间复杂度非常高，不适合处理大规模问题。
2. **动态规划方法**：考虑到递归回溯方法的效率问题，我们可以采用动态规划的方法来优化算法。动态规划方法的核心思想是从最后一个状态开始向前推导，逐步计算出每一个状态下的最优解，从而得出最终的最优解。
#### 动态规划详解
- **状态定义**：设 `P[X]` 表示从底层到点 `X` 可以摘到的最多桃子数，包含点 `X` 所能摘到的桃子数。
- **递推方程**：对于任意点 `X`，其最优解由与其相邻的两个点决定，即 `P[X] = max{P[Y], P[Z]} + w`，其中 `Y` 和 `Z` 分别为 `X` 的左侧和右侧的邻居点，`w` 为点 `X` 上的桃子数。
- **边界条件**：当处于最低层时，即 `X` 在最后一层时，`P[X]` 直接等于点 `X` 上的桃子数。
- **初始条件**：对于最底层的每个点，其值就是该点上的桃子数。
- **计算顺序**：从底层到顶层依次计算每个点的 `P[X]` 值。
#### 示例解析
假设桃树的结构如下所示：
```
A (1)
/ \
B(2) C(9)
/ \ / \
D(7) E(6) F(5)
```
- 对于点 `B`，`P[B] = max{P[D], P[E]} + 2 = max{7, 6} + 2 = 9`。
- 对于点 `C`，`P[C] = max{P[E], P[F]} + 9 = max{6, 5} + 9 = 15`。
- 最终，`P[A] = max{P[B], P[C]} + 1 = max{9, 15} + 1 = 16`。
因此，小猴子能够摘取的最多桃子数为16个。
#### 数据结构与实现
为了方便存储桃树的信息以及计算每个点的 `P[X]` 值，我们可以使用一个二维数组来表示桃树。
```c++
#define MAXLAYER 110
int peachtree[MAXLAYER][MAXLAYER] = {
{1, -1, -1, -1}, {2, 9, -1, -1}, {7, 6, 5, -1},
{2, 3, 6, 4}
};
int P[MAXLAYER][MAXLAYER];
```
其中 `peachtree` 数组用于存储桃树的结构，`P` 数组用于存储每个点 `X` 的 `P[X]` 值。
#### 参考代码
以下是一个使用 C++ 编写的示例程序，用于计算摘桃子问题的最大桃子数。
```c++
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
using namespace std;
#define MAXLAYER 110
int maxnum(int x, int y) // 返回2个整数中的大者
{
if (x > y)
return x;
else
return y;
}
int main()
{
int peachtree[MAXLAYER][MAXLAYER];
int P[MAXLAYER][MAXLAYER];
int i, j, k, n; // 读入数据
cin >> n;
k = 1; // 当前这层的节点数目
for (i = 0; i < n; i++) // n-i层的节点
{
for (j = 0; j < k; j++)
{
cin >> peachtree[j][n - i - 1];
}
k++;
}
// 初始化 P[x][0]
for (i = 0; i < n; i++)
{
P[i][0] = peachtree[i][0];
}
// 递推过程 P[x][y] = max{P[x][y-1], P[x+1][y-1]} + peachtree[x][y]
for (j = 1; j < n; j++) // i 是行号，j 是列号
{
for (i = 0; i + j < n; i++)
{
P[i][j] = maxnum(P[i][j - 1], P[i + 1][j - 1]) + peachtree[i][j];
}
}
// 输出结果
cout << "最多能摘到的桃子数为：" << P[0][n - 1] << endl;
return 0;
}
```
以上就是使用动态规划法解决摘桃子问题的详细步骤和示例代码。
