Fourier Theoretic Probabilistic Inference over Permutations

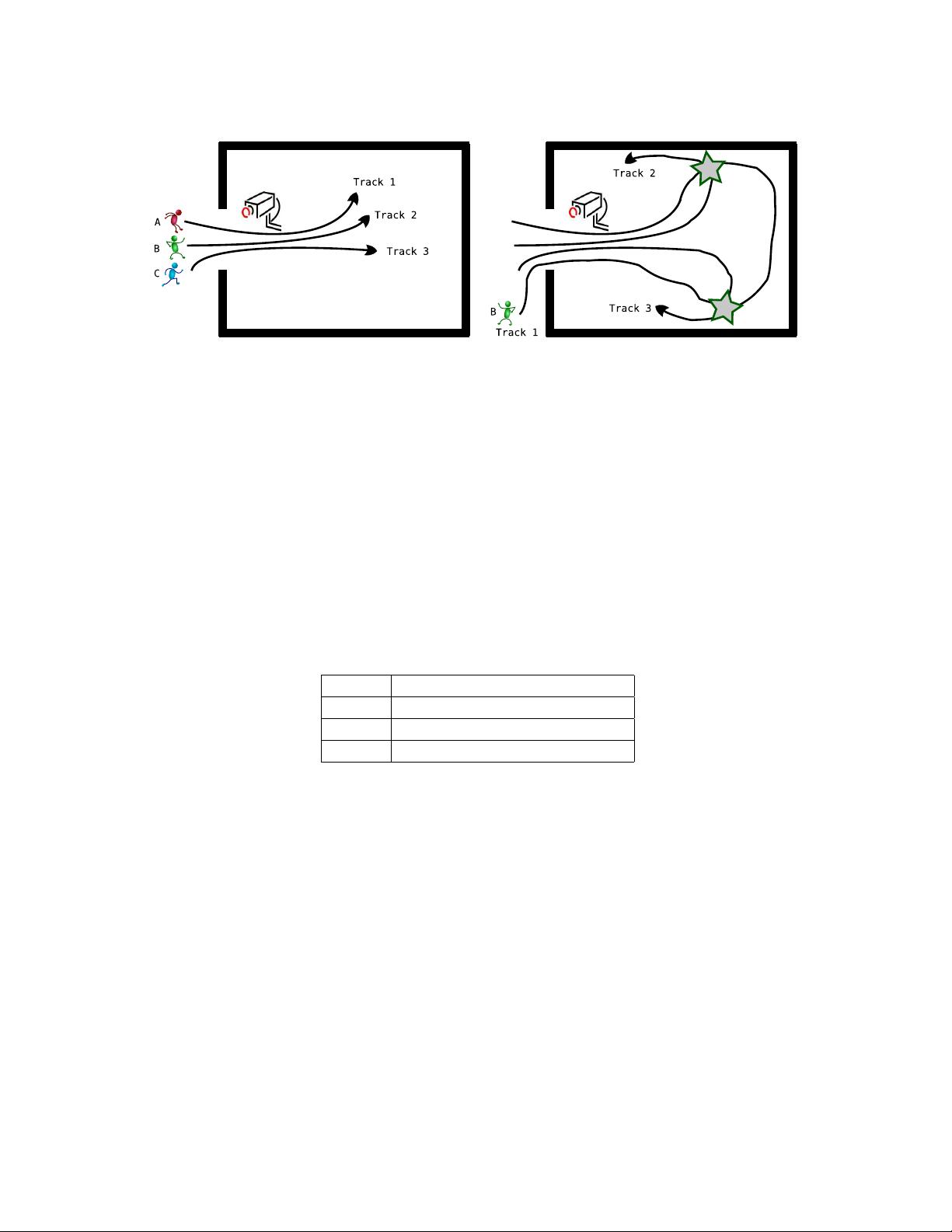
Permutations are ubiquitous in many real-world problems, such as voting, ranking, and data association. Representing uncertainty over permutations is challenging, since there are n! possibilities, and typical compact and factorized probability distribution representations, such as graphical models, cannot capture the mutual exclusivity constraints associated with permutations. In this paper, we use the “low-frequency” terms of a Fourier decomposition to represent distributions over permutations compactly. We present Kronecker conditioning, a novel approach for maintaining and updating these distributions directly in the Fourier omain, allowing for polynomial time bandlimited approximations. Low order Fourier-based approximations, however, may lead to functions that do not correspond to valid distributions. To address this problem, we present a quadratic program defined directly in the Fourier domain for projecting the approximation onto a relaxation of the polytope of legal marginal distributions. We demonstrate the effectiveness of our approach on a real camera-based multi-person tracking scenario. ### Fourier Theoretic Probabilistic Inference over Permutations #### Introduction This paper discusses a unique method for probabilistic inference over permutations, which are fundamental in a wide range of applications including voting, ranking, and data association. The challenge lies in representing uncertainty over permutations due to the factorial nature of their space (n!), making traditional probability distribution representations, like graphical models, insufficient. This work presents a novel approach using Fourier decomposition to compactly represent distributions over permutations. #### Key Concepts and Contributions **Permutations and Uncertainty Representation** - **Permutations**: A permutation is an arrangement of objects in a specific order. In the context of this paper, permutations are essential in solving problems related to voting, ranking, and data association. For instance, in multi-person tracking, determining the correct identity assignment (permutation) among observed individuals is crucial. - **Uncertainty Representation**: The paper addresses the difficulty in representing uncertainty over permutations, given the exponential number of possible arrangements (n!). Traditional compact representations like graphical models fail to capture the mutual exclusivity constraints inherent in permutations. **Fourier Decomposition** - **Low-Frequency Terms**: The authors utilize low-frequency terms from a Fourier decomposition to compactly represent distributions over permutations. This technique allows for a polynomial-time bandlimited approximation, making it feasible to work with permutations despite their combinatorial nature. - **Kronecker Conditioning**: This is a novel approach introduced for maintaining and updating distributions over permutations directly in the Fourier domain. It enables efficient computation while preserving the structure of the permutations. **Addressing Validity of Distributions** - **Approximations and Validity**: Low-order Fourier-based approximations can result in functions that do not correspond to valid probability distributions. This is a significant issue as the approximations must represent legitimate distributions. - **Quadratic Program in the Fourier Domain**: To address this problem, the paper proposes a quadratic program defined in the Fourier domain for projecting the approximation onto a relaxation of the polytope of legal marginal distributions. This ensures that the approximations remain valid and adhere to the constraints imposed by permutations. **Real-World Application** - **Multi-Person Tracking Scenario**: The effectiveness of the proposed approach is demonstrated through a real camera-based multi-person tracking scenario. This application showcases the practical utility of the method in addressing complex tracking challenges involving multiple identities. #### Detailed Analysis **Permutations and Challenges** Permutations are critical in various real-world problems, particularly in scenarios where the correct ordering or matching of entities is important. For example, in voting systems, understanding the preferences of voters through permutations can help in determining the outcome. Similarly, in multi-object tracking, permutations play a vital role in associating observations with individual objects or identities. **Fourier Decomposition and Kronecker Conditioning** The use of Fourier decomposition in this context provides a powerful tool for handling the large space of permutations. By focusing on low-frequency terms, the authors effectively reduce the complexity of the problem while preserving the essential characteristics of the distribution. Kronecker conditioning further enhances this approach by enabling updates directly in the Fourier domain, ensuring that the distribution remains accurate and efficient to compute. **Validity of Distributions** One of the key challenges addressed in the paper is ensuring that the approximations generated by the Fourier-based method remain valid probability distributions. The quadratic program in the Fourier domain serves as a projection mechanism, mapping the approximations back onto a valid distribution space. This step is crucial for maintaining the integrity of the results, especially when dealing with real-world applications where the validity of the distribution is paramount. **Conclusion** The paper "Fourier Theoretic Probabilistic Inference over Permutations" introduces a novel and effective method for handling uncertainty over permutations. By leveraging Fourier decomposition and innovative techniques like Kronecker conditioning, the authors provide a practical solution to a challenging problem in machine learning and probabilistic reasoning. The real-world application in multi-person tracking demonstrates the potential impact of this research in solving complex tracking challenges, particularly in scenarios requiring accurate identity management.