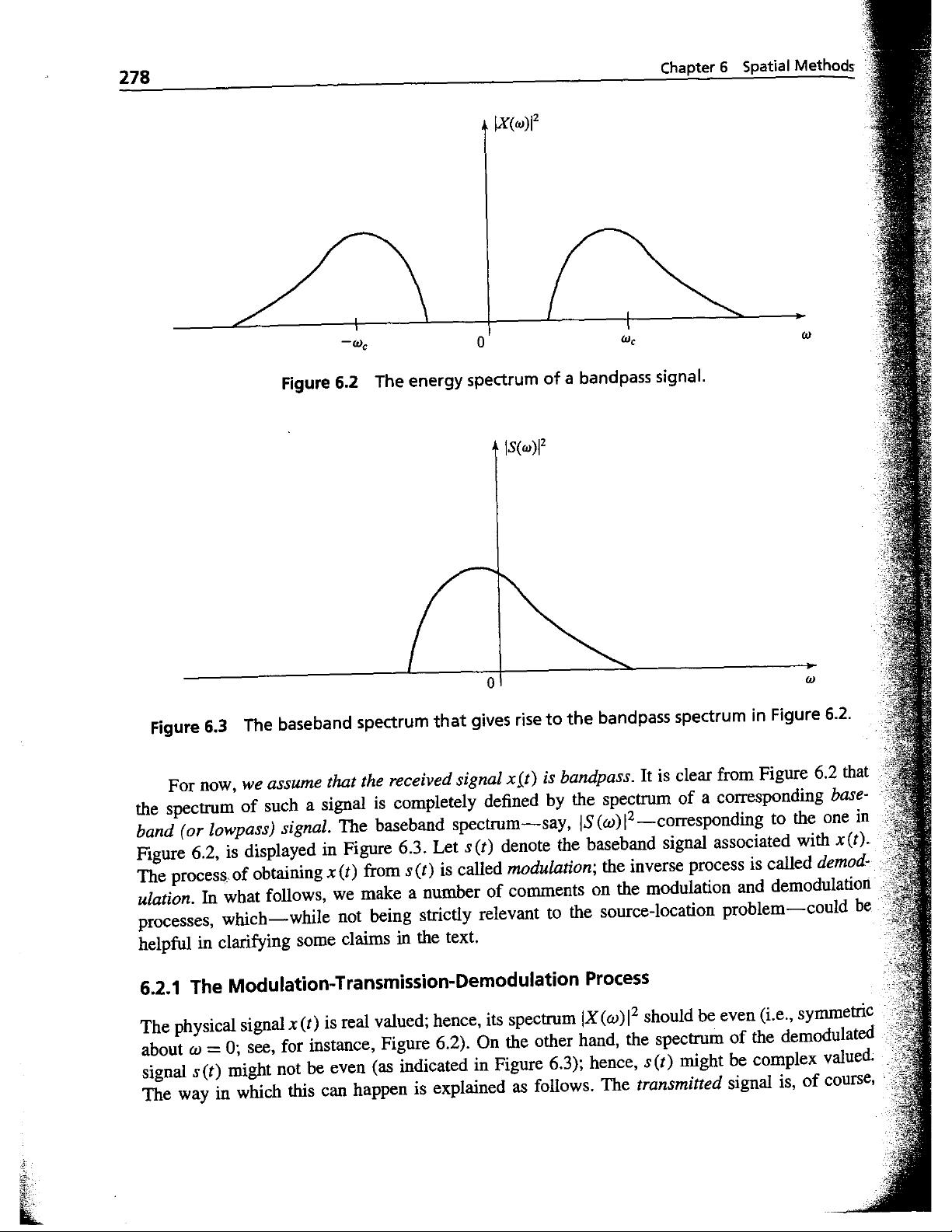
Spectral Analysis of Signals(Petre Stoica and Randolph Moses) 下半...

### Spectral Analysis of Signals: Spatial Methods - The Modulation-Transmission-Demodulation Process #### Introduction to Bandpass and Baseband Signals In the context of spectral analysis, understanding the modulation, transmission, and demodulation process is crucial for analyzing signals in various applications. In the given excerpt from Chapter 6 of "Spectral Analysis of Signals" by Petre Stoica and Randolph Moses, the focus is on spatial methods and specifically the modulation-transmission-demodulation process. This chapter delves into the characteristics of bandpass and baseband signals, which are fundamental concepts in signal processing. #### Bandpass Signals and Their Energy Spectrum A bandpass signal is a type of signal that has its frequency components confined within a specific range of frequencies, typically centered around a carrier frequency \( \omega_c \). The energy spectrum of a bandpass signal, as shown in Figure 6.2, is characterized by a concentration of energy around a particular center frequency, with the spectrum being symmetric about this center frequency. This symmetry is due to the real-valued nature of the physical signal \( x(t) \). #### Baseband Signals and Their Spectra Baseband signals, on the other hand, are low-frequency signals that have their frequency components starting from or close to zero frequency. The baseband spectrum of a signal, represented as \( S(\omega)^2 \), provides important information about the original bandpass signal. As depicted in Figure 6.3, the baseband spectrum is not necessarily symmetric, indicating that the baseband signal might be complex-valued. #### Modulation Process The modulation process involves transforming a baseband signal into a bandpass signal suitable for transmission over a communication channel. This transformation is achieved by multiplying the baseband signal \( s(t) \) by a cosine or sine wave, resulting in the bandpass signal \( x(t) \). \[ x(t) = 2a(t)\cos(\omega_c t + \phi(t)) \] Here, \( a(t) \) represents the amplitude of the baseband signal, \( \omega_c \) is the carrier frequency, and \( \phi(t) \) is the phase of the signal. The Fourier transform of \( x(t) \), denoted as \( X(\omega) \), shows that the spectrum of the modulated signal consists of two impulses shifted to \( \omega_c \) and \( -\omega_c \): \[ X(\omega) = S(\omega - \omega_c) + S^*(-(\omega + \omega_c)) \] The asterisk (*) denotes the complex conjugate. The modulation process translates the spectrum of the baseband signal to higher frequencies, making it suitable for transmission over a communication channel. #### Transmission Channel Characteristics The characteristics of the transmission channel (or propagation medium) can significantly affect the received signal. Often, the channel introduces asymmetry in the spectrum around the carrier frequency \( \omega_c \). This asymmetry can lead to the received bandpass signal having an associated baseband spectrum that is not even, meaning it does not have the same shape on both sides of the center frequency. Consequently, the demodulated received signal may become complex-valued. #### Demodulation Process The demodulation process is the inverse of modulation and involves extracting the baseband signal from the received bandpass signal. This extraction can be achieved by multiplying the received signal by the same carrier frequency used during modulation and then filtering out the high-frequency components. If the received signal is complex-valued, the demodulation process may involve additional steps to recover the original baseband signal accurately. #### Importance of Complex-Valued Signals in Spectral Estimation The text highlights the importance of considering complex-valued signals in spectral estimation problems. The modulation-transmission-demodulation process often results in complex-valued signals, especially when the transmission channel introduces asymmetry in the spectrum. Understanding the characteristics of these signals is crucial for accurately estimating their spectra and extracting meaningful information. #### Conclusion In summary, the modulation-transmission-demodulation process is a fundamental concept in the analysis of bandpass and baseband signals. The process involves transforming a low-frequency baseband signal into a bandpass signal suitable for transmission, and then extracting the original baseband signal from the received bandpass signal. Understanding the characteristics of these signals, particularly the effects of the transmission channel on the spectrum, is essential for effective spectral analysis and estimation.