解析几何23-mathtype.pdf

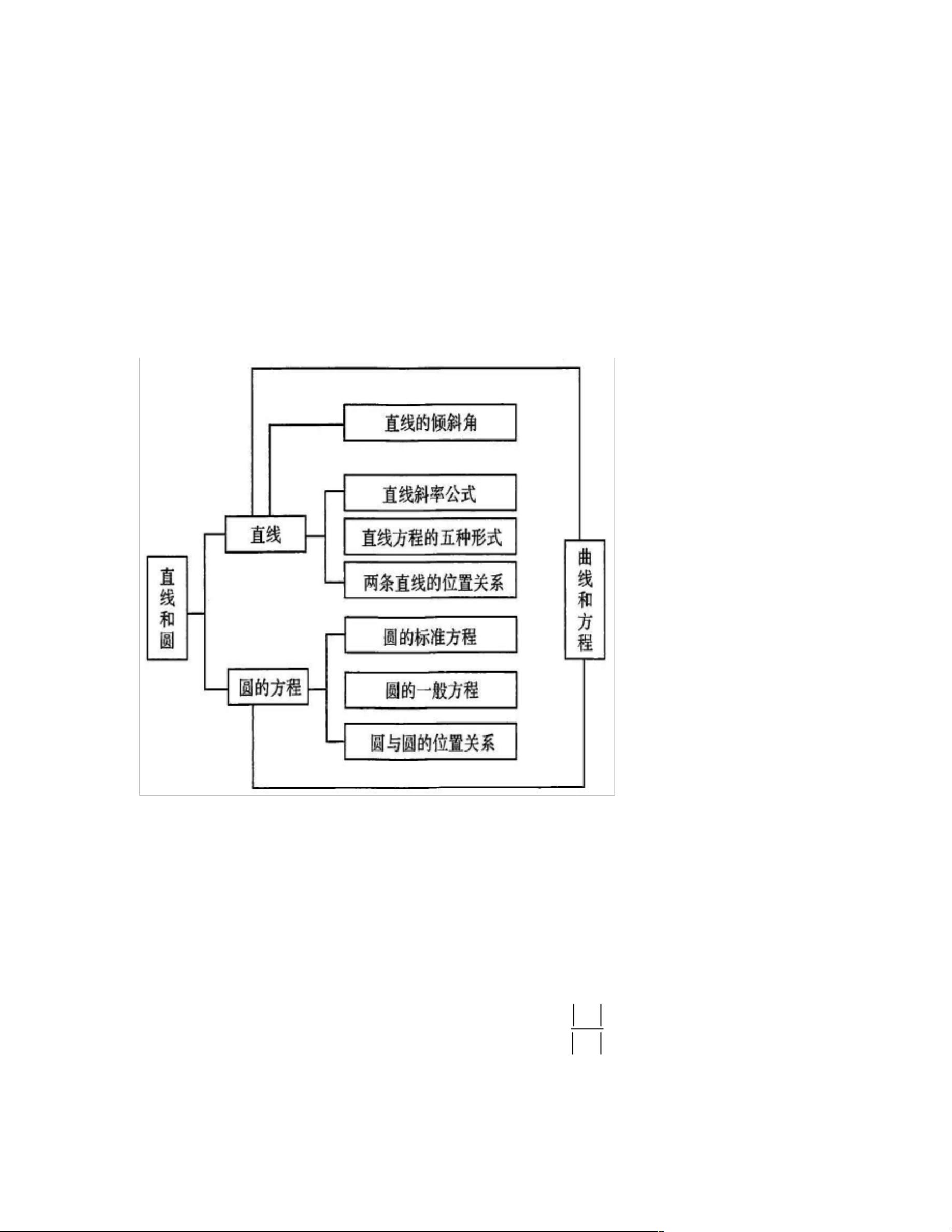
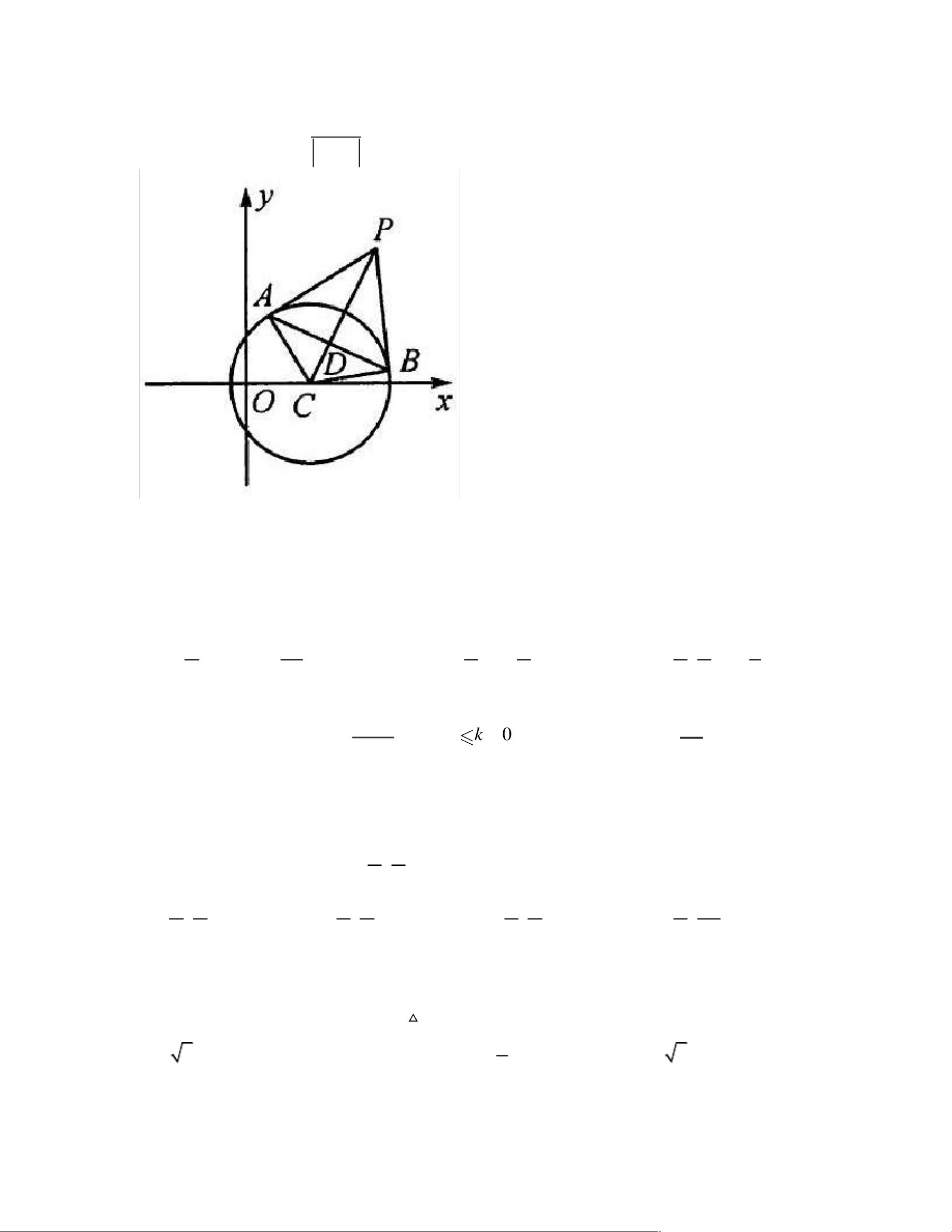
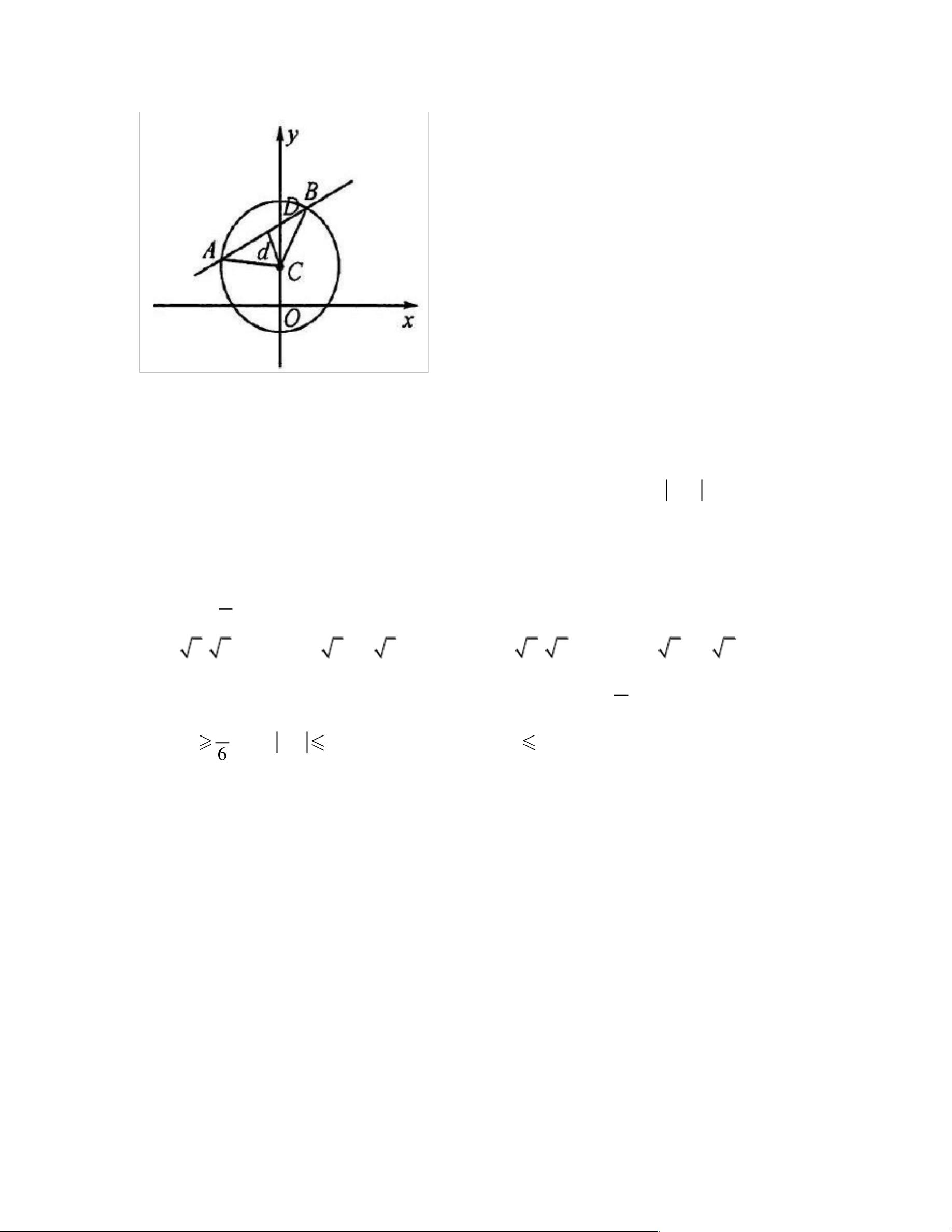
在解析几何中，直线与圆的研究是基础且重要的部分，它们是初中到高中的核心内容。引入坐标系后，可以通过方程式来描述直线和圆，从而利用代数方法探究几何图形之间的位置关系，并分析直线方程和圆的方程所揭示的性质。这体现了数形结合的思想。 我们关注圆的切线方程。对于一个圆，其方程一般形式为 (x-a)^2 + (y-b)^2 = r^2，其中 (a, b) 是圆心坐标，r 是半径。如果一个点P(0,0)在圆上，则过P的切线方程可以通过将点P的坐标代入圆的方程来确定。例如，如果点P在圆(x-a)^2 + (y-b)^2 = r^2上，那么切线方程为200xaxaybybr- - - - = 0。 对于点P(0,0)在圆外的情况，我们可以找到两条切线，切点分别是A和B。这时，切点弦AB的方程同样是200xaxaybybr- - - - = 0。这个方程反映了从点P出发的两条切线与圆的交点A和B的连线特征。 接下来，我们探讨阿波罗尼斯圆。阿波罗尼斯圆是由平面上两点A和B决定的一类特殊圆，其中任意一点P满足与A和B的距离之比为常数λ（λ>0且λ≠1）。当λ=1时，轨迹不再是圆而是线段AB的中垂线。阿波罗尼斯圆的直径可以表示为221aλλ -，其中a是线段AB的长度。 进阶提升部分，我们通过例题来强化理解。例如，第一道题目考察直线的倾斜角范围。直线的斜率与倾斜角α之间有关系k=tanα，由此可以求出直线的倾斜角。第二题则涉及到两条过定点的动直线的交点P形成的三角形PAB的面积最大值问题，关键在于发现P点位于以AB为直径的圆上，利用基本不等式解决。 第三题为多选题，涉及圆的几何性质。题目中给出了圆心C和一条过点(0,3)的直线l与圆交于A和B两点，且弦AB的长度为圆半径的3/2倍。根据垂径定理，可以计算出圆心到直线l的距离，再根据直线l可能的斜率存在与否，列出可能的方程。 总结来说，解析几何中的直线与圆部分主要包含以下几个知识点： 1. 圆的方程和性质。 2. 直线的方程和斜率与倾斜角的关系。 3. 圆的切线方程。 4. 阿波罗尼斯圆的概念及其性质。 5. 直线与圆的综合问题，如交点、切点、面积最大值等。 这些知识点不仅要求我们掌握基础的代数运算，还需要灵活运用几何直觉和推理，以及熟练应用数学公式和定理。在解题过程中，正确理解和应用这些概念是解决问题的关键。