abaqus动力学有限元分析资料

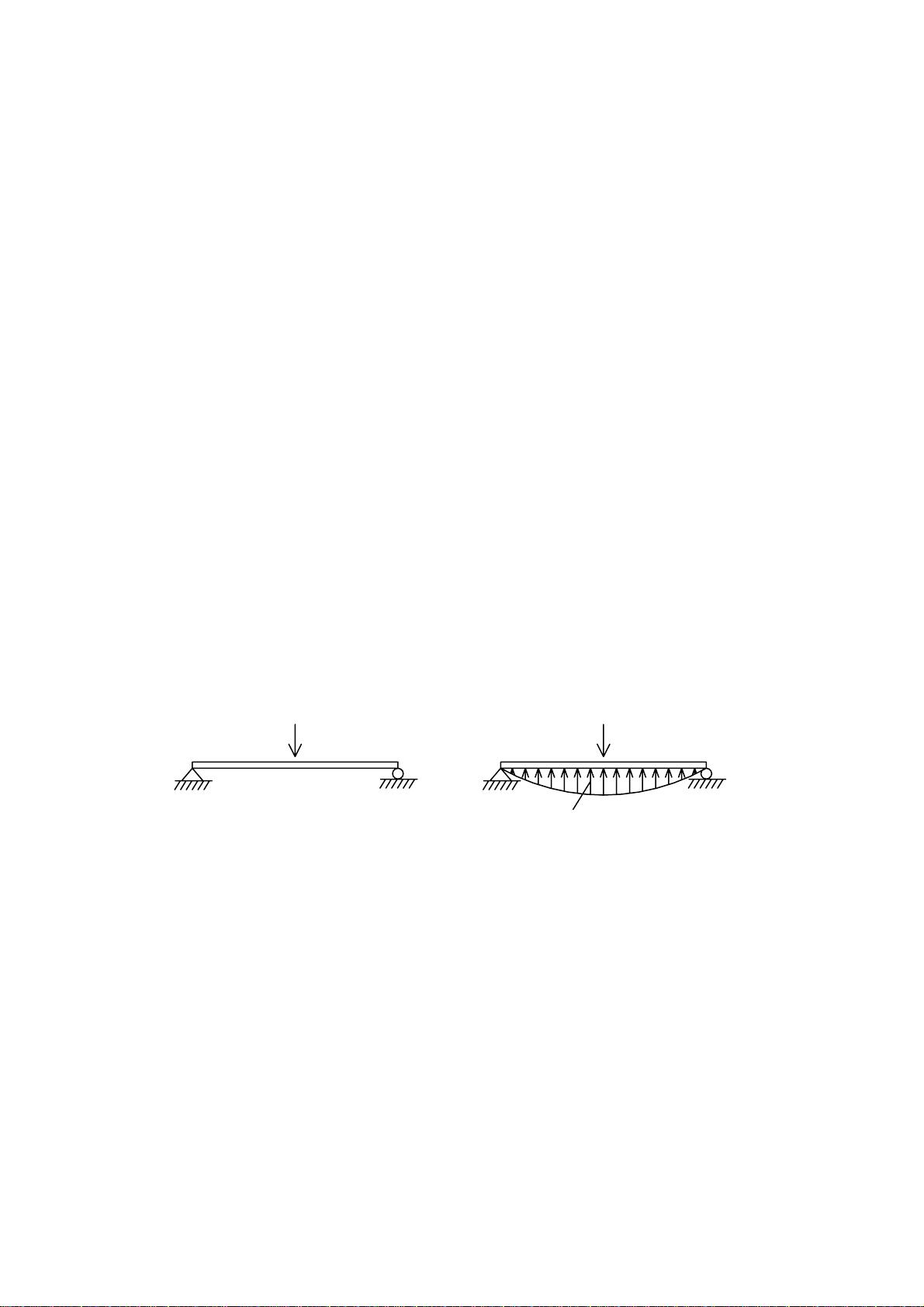
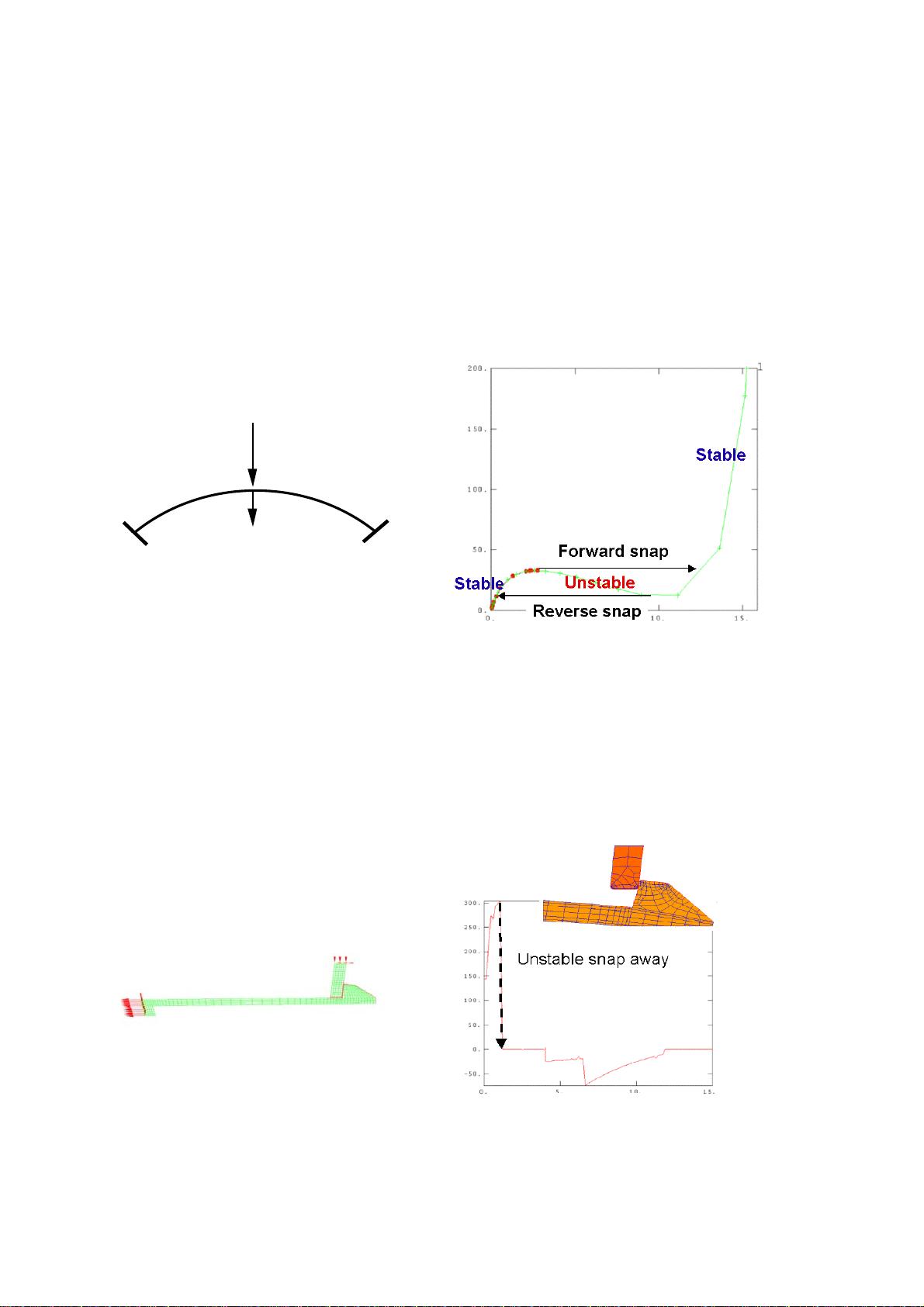
《深入解析：Abaqus动力学有限元分析》 标题和描述揭示了关于Abaqus动力学有限元分析的关键知识点，这一领域涉及复杂的结构动力学分析，尤其在现代工程设计中占据重要地位。下面，我们将从动力学问题的概述、结构特征值提取、模态叠加法、阻尼、稳态和瞬态动力学分析、基础运动以及加速度运动的基线校准等方面进行详细探讨。 ### 动力学问题概述 动力学问题主要关注的是结构在动力荷载下的响应，包括位移、内力、应力和应变等随时间的变化。动力荷载的特点在于其大小、方向或作用点随时间而改变，这使得动力学分析相较于静力分析更加复杂。在动力学分析中，不仅需要考虑外部荷载，还要考虑到结构的加速度产生的惯性力，这是动力学问题与静力问题的重要区别之一。当惯性力成为内部弹性力平衡的主要组成部分时，结构的动力特性变得至关重要。 ### 结构特征值的提取 结构特征值，尤其是固有频率和模态振型，是动力学分析的基础。特征值的求解方法多种多样，包括直接求解法、迭代法等。不同的求解器有不同的适用范围和精度，理解它们之间的差异有助于选择最合适的算法。重复的特征频率处理、预加载条件下的频率分析以及复特征频率的求解，这些都是高级动力学分析中不可或缺的部分。 ### 模态叠加法 模态叠加法是一种常用的线性动力学分析方法，它基于结构的模态振型和对应的固有频率，将复杂的问题简化为多个独立的单自由度系统。这种方法在分析中能够有效减少计算量，特别是在处理大型结构时，其优势尤为明显。通过合理应用模态叠加法，可以准确预测结构在各种动态荷载下的响应。 ### 阻尼 阻尼是动力学分析中的关键因素，它影响着结构的振动衰减和能量耗散。Abaqus提供了多种阻尼模型和定义阻尼的方式，包括比例阻尼、粘性阻尼和非线性阻尼等。正确设置阻尼参数对于模拟实际物理过程、提高仿真精度至关重要。 ### 稳态和瞬态动力学分析 稳态动力学分析通常用于处理周期性的动力荷载，如风荷载、海浪荷载等，分析结构的谐振响应。瞬态动力学分析则关注结构在非周期性动力荷载下的响应，例如地震、爆炸等事件。两种分析类型都需要精确的荷载和边界条件定义，以及合适的求解策略。 ### 基础运动和加速度运动的基线校准 基础运动是指支撑结构的地面运动，这在地震分析中尤为重要。Abaqus提供了定义基础运动的功能，允许用户导入实测地震记录或自定义运动曲线。加速度运动的基线校准则是为了消除初始位移和速度的影响，确保分析结果的准确性。这一过程在分析振动控制设备的有效性时特别关键。 Abaqus动力学有限元分析是一个综合性和技术性极强的领域，它涵盖了从基本的动力学理论到高级分析技术的广泛内容。通过深入理解和应用上述知识点，工程师和研究人员能够更准确地评估和优化结构在复杂动力环境下的性能，从而推动工程设计的进步和发展。