3月24日直播《一节课掌握机器学习经典算法-支持向量机》.pdf

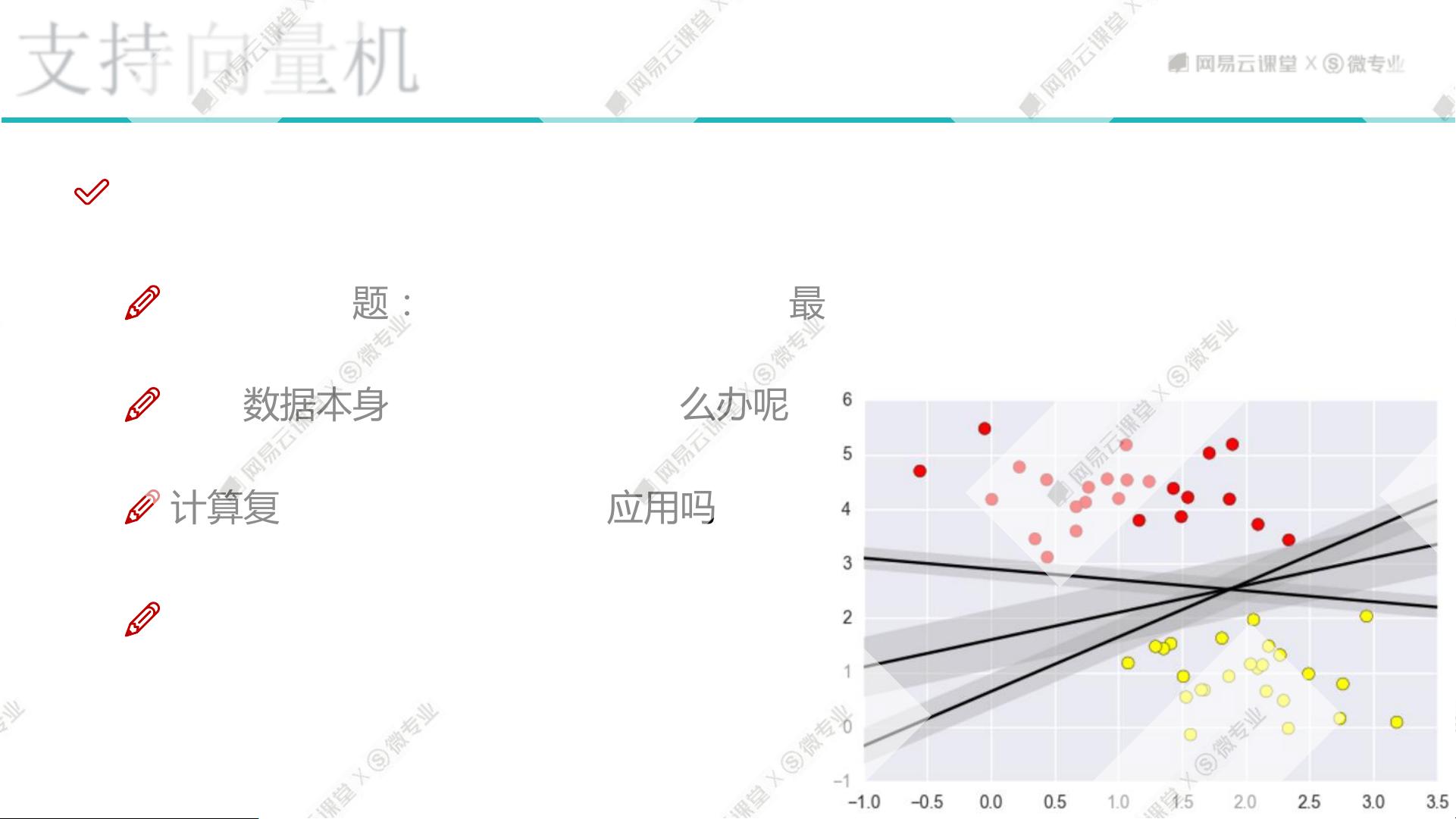
### 机器学习经典算法——支持向量机(Support Vector Machine, SVM) #### 一、引言 支持向量机（SVM, Support Vector Machine）是一种非常强大的机器学习算法，广泛应用于分类与回归任务中。其核心思想是寻找一个最优的决策边界（即超平面），使得正负样本间的边际最大化。本篇文章将详细介绍支持向量机的基本概念、数学原理以及其实现过程，并通过一个具体的例子来展示其工作流程。 #### 二、基础知识回顾 1. **决策边界**：在分类问题中，决策边界是指能够将不同类别的样本正确分开的超平面。 2. **支持向量**：离决策边界最近的样本点被称为支持向量。这些样本点对于确定决策边界至关重要。 3. **最大边际**：SVM 的目标是找到一个具有最大边际的决策边界，以提高模型的泛化能力。 #### 三、支持向量机的基本原理 1. **基本问题** - **决策边界的选择**：SVM 的目标是选择一个决策边界，使得正负样本间的距离（即边际）最大化。 - **非线性可分问题**：当数据集中的样本难以通过简单的线性决策边界分开时，可以通过引入核函数将数据映射到更高维度的空间中，使之变得线性可分。 2. **距离计算** - **点到直线的距离**：支持向量机通过计算样本点到决策边界的距离来确定最优决策边界。这一距离的计算公式为 \(\frac{|w^T x + b|}{\|w\|}\)，其中 \(w\) 是权重向量，\(b\) 是偏置项，\(x\) 是样本点。 3. **数据标签定义** - **样本标签**：在 SVM 中，每个样本 \(X_i\) 都有一个对应的标签 \(Y_i\)，当 \(X_i\) 为正例时 \(Y_i = +1\)，当 \(X_i\) 为负例时 \(Y_i = -1\)。 4. **目标函数** - **优化目标**：SVM 的目标是找到一个超平面，使得离该超平面最近的支持向量到超平面的距离最大化。 - **放缩变换**：为了简化计算，可以对决策方程进行放缩，使其结果的绝对值大于或等于 1。 5. **优化问题的求解** - **拉格朗日乘子法**：为了解决带有约束条件的优化问题，SVM 使用拉格朗日乘子法。 - **求极大值问题转换**：SVM 将求极大值问题转换为求极小值问题，即最小化 \(\frac{1}{2} w^T w\)。 - **对偶问题**：通过对原始问题进行求解，可以得到对偶问题的形式，进而更容易地求解最优解。 #### 四、支持向量机的实现步骤 1. **构建目标函数**：根据给定的数据集和标签，构建目标函数。 2. **拉格朗日乘子法的应用**：利用拉格朗日乘子法将原问题转换为对偶问题。 3. **求解对偶问题**：通过求解对偶问题来获得最优解。 4. **计算支持向量**：确定哪些样本点是支持向量。 5. **预测新样本**：使用训练好的模型对新样本进行分类预测。 #### 五、示例分析 假设我们有一组数据集，包含三个样本点：正例 \(X_1(3, 3)\), \(X_2(4, 3)\)，负例 \(X_3(1, 1)\)。 1. **构造拉格朗日函数**：根据给定的数据集，构造拉格朗日函数，并通过求解对偶问题来确定 \(\alpha\) 值。 2. **求解 \(\alpha\) 值**：对 \(\alpha_1\) 和 \(\alpha_2\) 求偏导，并令偏导等于 0，从而得到 \(\alpha\) 的值。 3. **计算权重向量 \(w\) 和偏置项 \(b\)**：根据 \(\alpha\) 的值，计算出 \(w\) 和 \(b\)。 4. **决策边界方程**：最终得到的决策边界方程为 \(0.5x_1 + 0.5x_2 - 2 = 0\)。 #### 六、扩展：软间隔和支持向量机 1. **软间隔的概念**：在现实世界中，数据往往包含噪声，硬间隔（即要求所有样本都严格位于决策边界的一侧）可能无法很好地拟合数据。因此，引入软间隔的概念，允许部分样本跨越决策边界。 2. **松弛因子**：为了解决非严格可分问题，引入松弛因子 \(\xi_i\)，并将之加入到目标函数中，以允许部分样本点违反决策边界。 3. **软间隔优化问题**：在软间隔的情况下，优化问题变为最小化 \(\frac{1}{2} w^T w + C \sum_{i=1}^n \xi_i\)，其中 \(C\) 是惩罚系数，用于平衡误差项和边际大小。 #### 七、核变换技术 1. **低维不可分问题**：当数据在低维空间中不可分时，可以采用核变换技术将其映射到高维空间，使之变得线性可分。 2. **核函数的选择**：常用的核函数包括线性核、多项式核、高斯径向基核等。不同的核函数适用于不同类型的数据分布。 3. **核技巧**：通过使用核技巧，可以在不显式计算高维空间中的特征向量的情况下，完成数据的映射。 #### 八、总结 支持向量机是一种强大且灵活的机器学习算法，它通过寻找最大边际的决策边界来提高模型的泛化能力。通过上述介绍，我们了解到支持向量机的基本原理、数学推导过程及其在解决非线性可分问题时的应用方法。此外，通过引入软间隔和核变换技术，SVM 能够处理更为复杂的分类问题，从而在实际应用中展现出优异的性能。