IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 16, NO. 2, FEBRUARY 2007 349
Kernel Regression for Image Processing
and Reconstruction
Hiroyuki Takeda, Student Member, IEEE, Sina Farsiu, Member, IEEE, and Peyman Milanfar, Senior Member, IEEE
Abstract—In this paper, we make contact with the field of non-
parametric statistics and present a development and generalization
of tools and results for use in image processing and reconstruc-
tion. In particular, we adapt and expand kernel regression ideas
for use in image denoising, upscaling, interpolation, fusion, and
more. Furthermore, we establish key relationships with some pop-
ular existing methods and show how several of these algorithms,
including the recently popularized bilateral filter, are special cases
of the proposed framework. The resulting algorithms and analyses
are amply illustrated with practical examples.
Index Terms—Bilateral filter, denoising, fusion, interpolation,
irregularly sampled data, kernel function, kernel regression, local
polynomial, nonlinear filter, nonparametric, scaling, spatially
adaptive, super-resolution.
I. INTRODUCTION
T
HE ease of use and cost effectiveness have contributed to
the growing popularity of digital imaging systems. How-
ever, inferior spatial resolution with respect to the traditional
film cameras is still a drawback. The apparent aliasing effects
often seen in digital images are due to the limited number of
CCD pixels used in commercial digital cameras. Using denser
CCD arrays (with smaller pixels) not only increases the pro-
duction cost, but also results in noisier images. As a cost-effi-
cient alternate, image processing methods have been exploited
through the years to improve the quality of digital images. In
this paper, we focus on regression methods that attempt to re-
cover the noiseless high-frequency information corrupted by the
limitations of imaging systems, as well as the degradations pro-
cesses such as compression.
We study regression, as a tool not only for interpolation of
regularly sampled frames (up-sampling), but also for restoration
and enhancement of noisy and possibly irregularly sampled im-
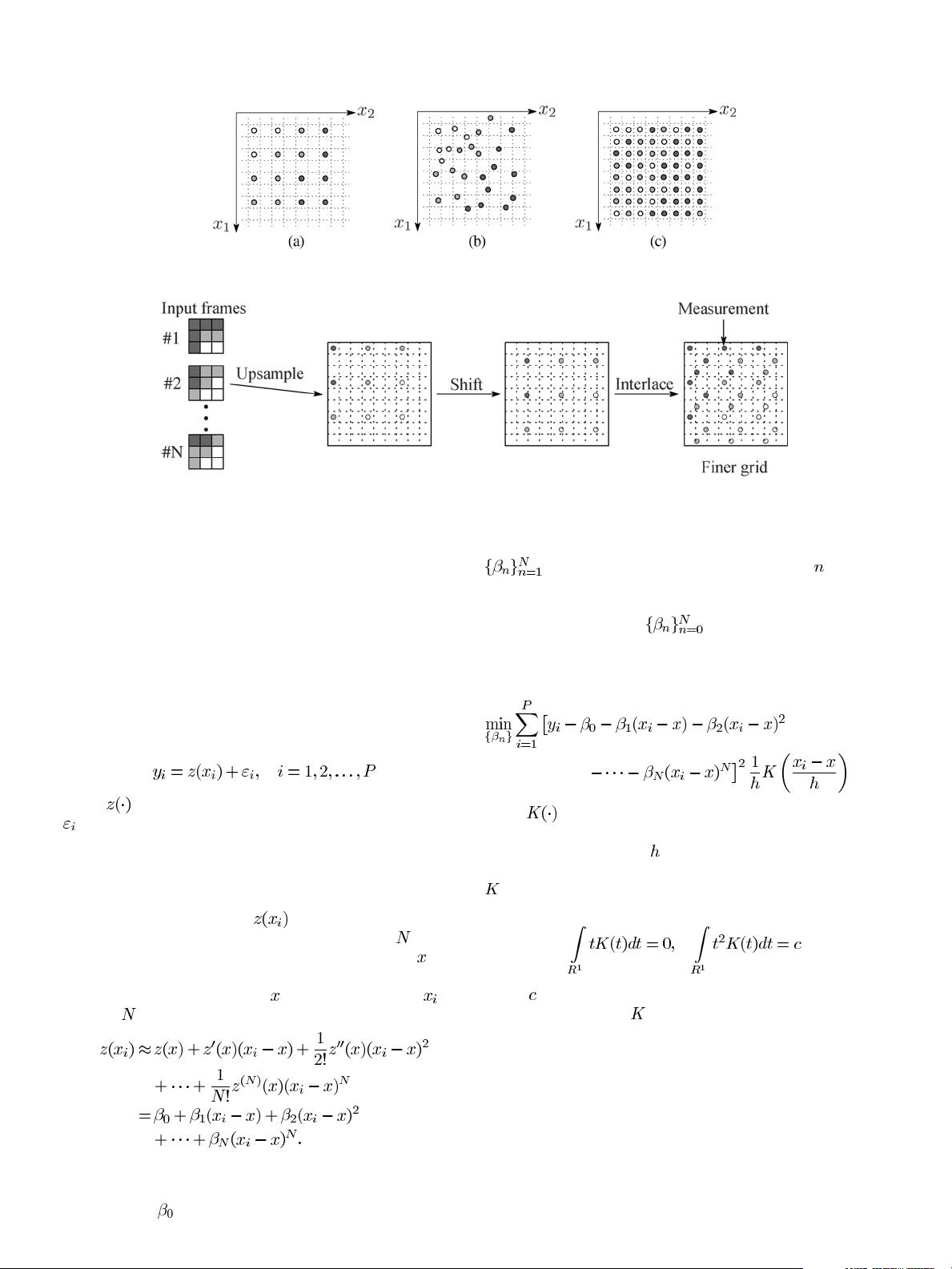
ages. Fig. 1(a) illustrates an example of the former case, where
we opt to upsample an image by a factor of two in each direc-
tion. Fig. 1(b) illustrates an example of the latter case, where
an irregularly sampled noisy image is to be interpolated onto a
Manuscript received December 15, 2005; revised August 1, 2006. This work
was supported in part by the U.S. Air Force under Grant F49620-03-1-0387
and in part by the National Science Foundation Science and Technology Center
for Adaptive Optics, managed by the University of California at Santa Cruz
under Cooperative Agreement AST-9876783. The associate editor coordinating
the review of this manuscript and approving it for publication was Dr. Tamas
Sziranyi.
The authors are with the Electrical Engineering Department, University of
California Santa Cruz, Santa Cruz CA 95064 USA (e-mail: htakeda@soe.ucsc.
edu; farsiu@soe.ucsc.edu; milanfar@soe.ucsc.edu).
Color versions of one or more of the figures in this paper are available online
at http://ieeexplore.ieee.org.
Software implementation available at http://www.soe.ucsc.edu/~htakeda.
Digital Object Identifier 10.1109/TIP.2006.888330
high resolution grid. Besides inpainting applications [1], inter-
polation of irregularly sampled image data is essential for ap-
plications such as multiframe super-resolution, where several
low-resolution images are fused (interlaced) onto a high-reso-
lution grid [2]. Fig. 2 represents a block diagram representation
of such super-resolution algorithm. We note that “denoising” is
a special case of the regression problem where samples at all de-
sired pixel locations are given [illustrated in Fig. 1(c)], but these
samples are corrupted, and are to be restored.
Contributions of this paper are the following. 1) We describe
and propose
kernel regression as an effective tool for both de-
noising and interpolation in image processing, and establish its
relation with some popular existing techniques. 2) We propose a
novel adaptive generalization of kernel regression with excellent
results in both denoising and interpolation (for single or multi-
frame) applications.
This paper is structured as follows. In Section II, we will
briefly describe the kernel regression idea for univariate data,
and review several related concepts. Furthermore, the classic
framework of kernel regression for bivariate data and intuitions
on related concepts will also be presented. In Section III, we
extend and generalize this framework to derive a novel data-
adapted kernel regression method. Simulation on both real and
synthetic data are presented in Section IV, and Section V con-
cludes this paper. We begin with a brief introduction to the no-
tion of kernel regression.
II. C
LASSIC KERNEL REGRESSION AND
ITS PROPERTIES
In this section, we formulate the classical kernel regression
method, provide some intuitions on computational efficiency,
as well as weaknesses of this method, and motivate the devel-
opment of more powerful regression tools in the next section.
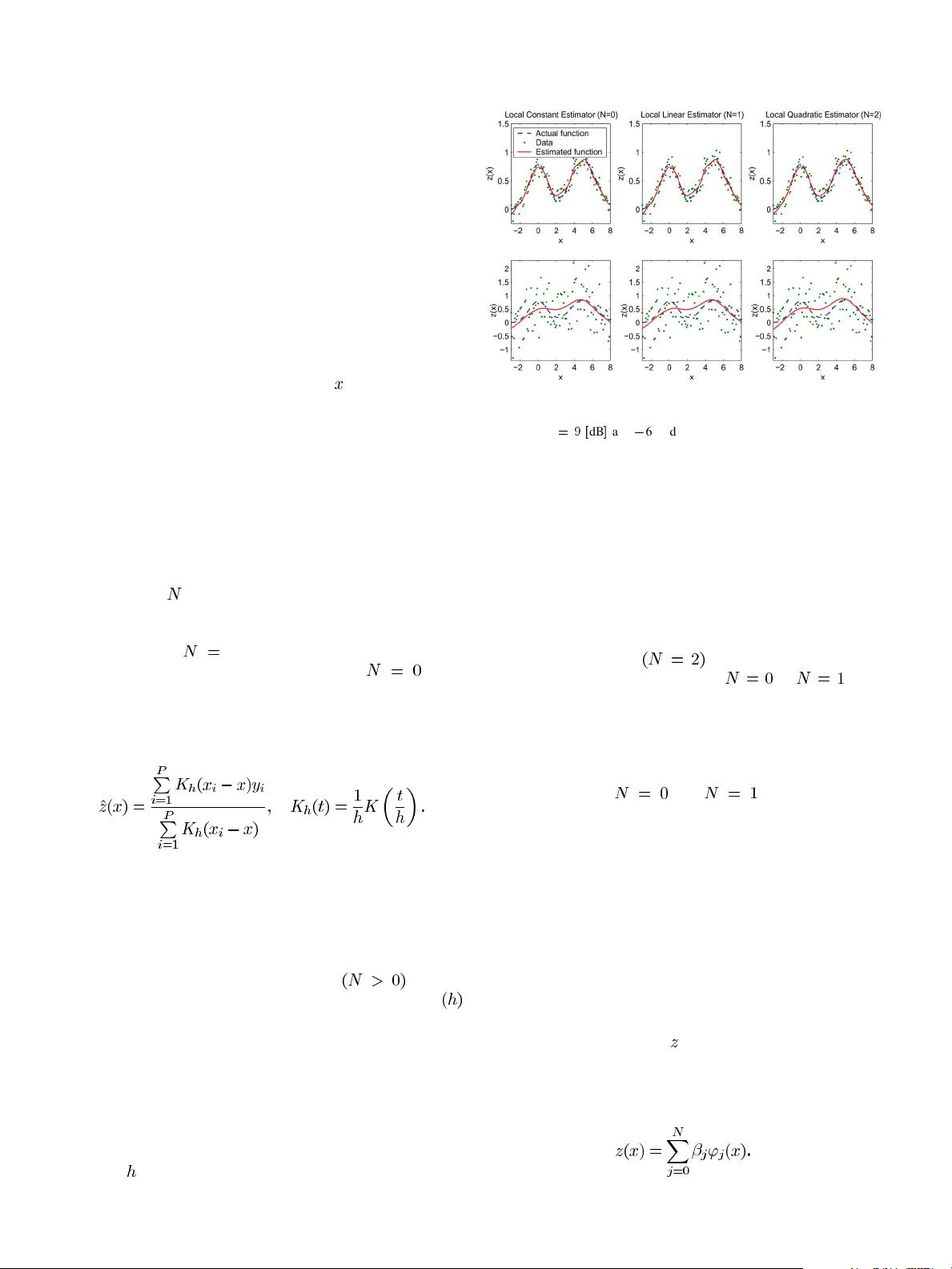
A. Kernel Regression in 1-D
Classical parametric image processing methods rely on a spe-
cific model of the signal of interest and seek to compute the pa-
rameters of this model in the presence of noise. Examples of
this approach are presented in diverse problems ranging from
denoising to upscaling and interpolation. A generative model
based upon the estimated parameters is then produced as the
best estimate of the underlying signal.
In contrast to the parametric methods, nonparametric
methods rely on the data itself to dictate the structure of the
model, in which case this implicit model is referred to as a
regression function [3]. With the relatively recent emergence
of machine learning methods, kernel methods have become
well-known and used frequently for pattern detection and
discrimination problems [4]. Surprisingly, it appears that the
corresponding ideas in nonparametric estimation—what we
1057-7149/$25.00 © 2006 IEEE