MIT 麻省理工 算法课程-第六节-讲义(经典!)
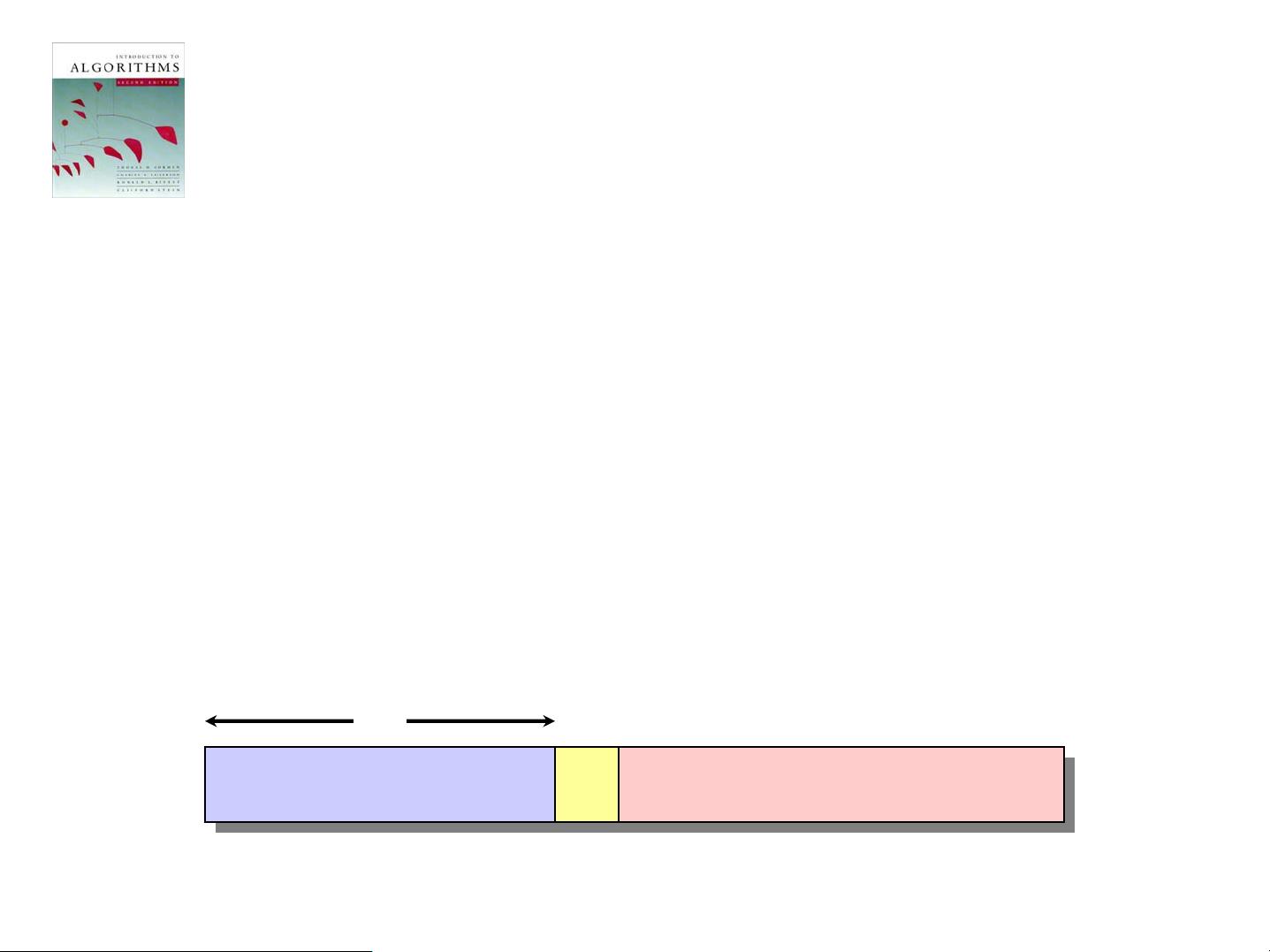
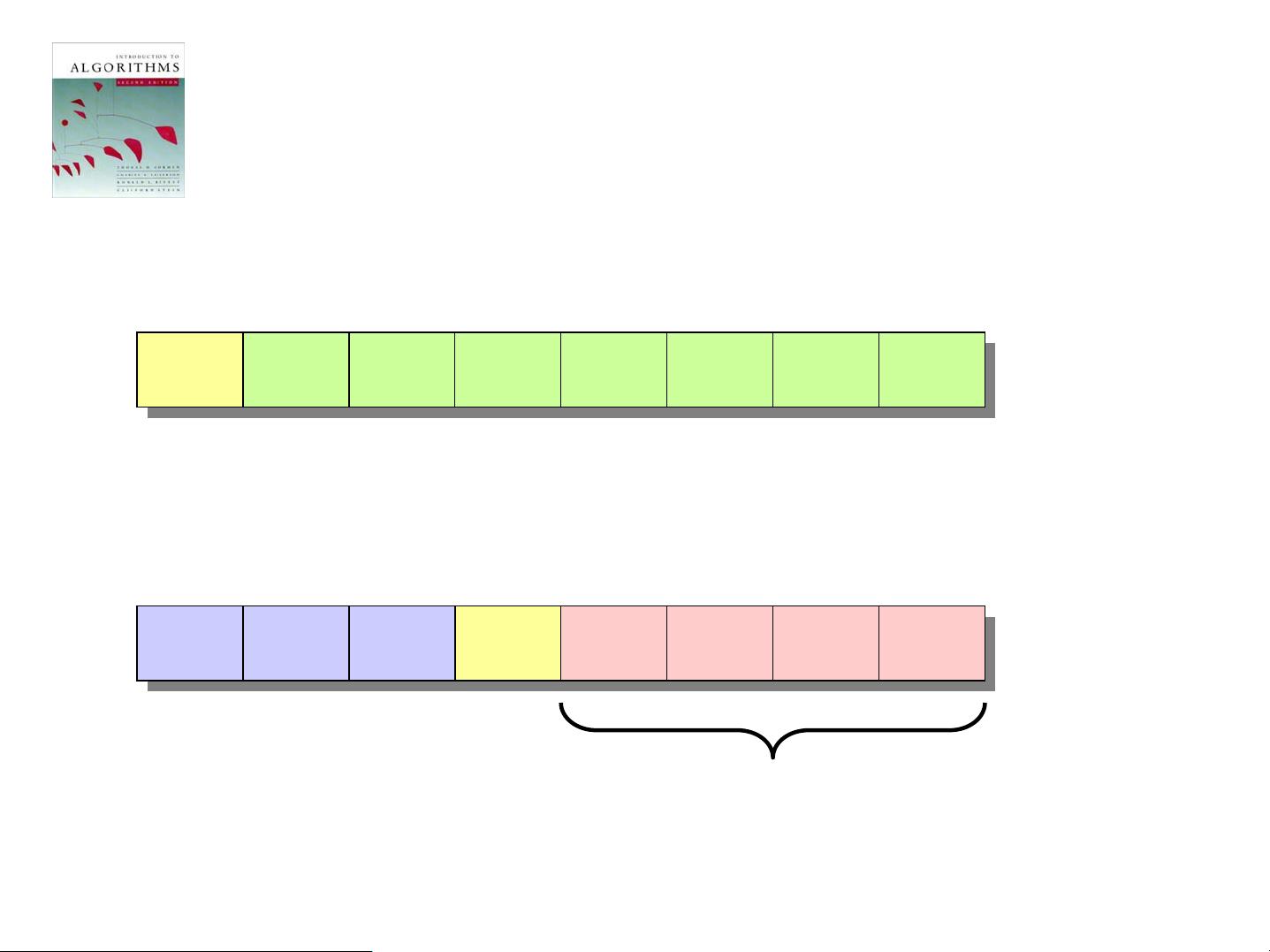
### MIT麻省理工算法课程-第六节:序统计与中位数 在MIT的算法课程中,第六节的内容深入探讨了序统计(Order Statistics)这一关键主题,特别是中位数的计算方法。序统计指的是在一个元素集合中找到第i小的元素的过程,这涉及到排序、搜索以及随机化算法的应用。 #### 序统计的基本概念 - **定义**:序统计的目标是确定一个由n个元素构成的序列中的第i小的元素,即排名为i的元素。 - 当i=1时,我们寻找的是最小值; - 当i=n时,目标是最小值; - 当i等于`(n+1)/2`或`[(n+1)/2]`时,则是在找中位数。 - **朴素算法**:最直观的方法是先对所有元素进行排序,然后直接访问第i个位置的元素。然而,这种方法的时间复杂度为Θ(n log n),使用如归并排序或堆排序等算法实现,但不适合用快速排序来解决,因为后者在最坏情况下可能退化至O(n^2)。 #### 随机化分治算法 一种更高效的解决方案是采用随机化分治算法,这种方法能够在期望时间上达到线性性能。 ##### RAND-SELECT算法概览 RAND-SELECT算法是基于随机化分治策略设计的,其核心步骤包括: 1. **检查边界条件**:如果数组大小为1,直接返回该元素。 2. **随机划分**:选择一个随机的轴心元素,对数组进行划分,使得轴心左边的元素都小于它,右边的元素都大于它。 3. **确定轴心的秩**:计算轴心元素的秩(即它在有序数组中的位置)。 4. **递归调用**: - 如果目标秩与轴心的秩相等,返回轴心元素。 - 如果目标秩小于轴心的秩,递归地在左半部分查找。 - 如果目标秩大于轴心的秩,递归地在右半部分查找,并更新目标秩。 ##### 分析与实例 算法的效率依赖于随机划分的质量。在理想情况下,每次都能得到接近均匀的分割,导致算法的时间复杂度为Θ(n)。然而,在最坏的情况下,如果每次都得到极不平衡的分割,时间复杂度会恶化至Θ(n^2),甚至比排序还要差。 #### 预期时间分析 对于RAND-SELECT算法,其运行时间的期望分析类似于随机化快速排序,但存在细微差别。通过定义指示随机变量Xk,我们可以跟踪特定类型的分割事件,进而估计平均情况下的运行时间。尽管最坏情况下的时间复杂度不理想,但随机化算法在实际应用中往往表现出良好的平均性能。 MIT算法课程的第六节深入介绍了序统计的理论与实践,特别是中位数的高效计算方法。通过理解随机化分治策略,我们不仅能处理基本的排序问题,还能有效地应对更复杂的统计查询需求。这一课程强调了算法设计的灵活性和效率的重要性,展示了随机性和分治策略在算法优化中的关键作用。



剩余29页未读,继续阅读
- 粉丝: 1
- 资源: 12
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功
评论0