浅谈最大子矩阵问题.docx

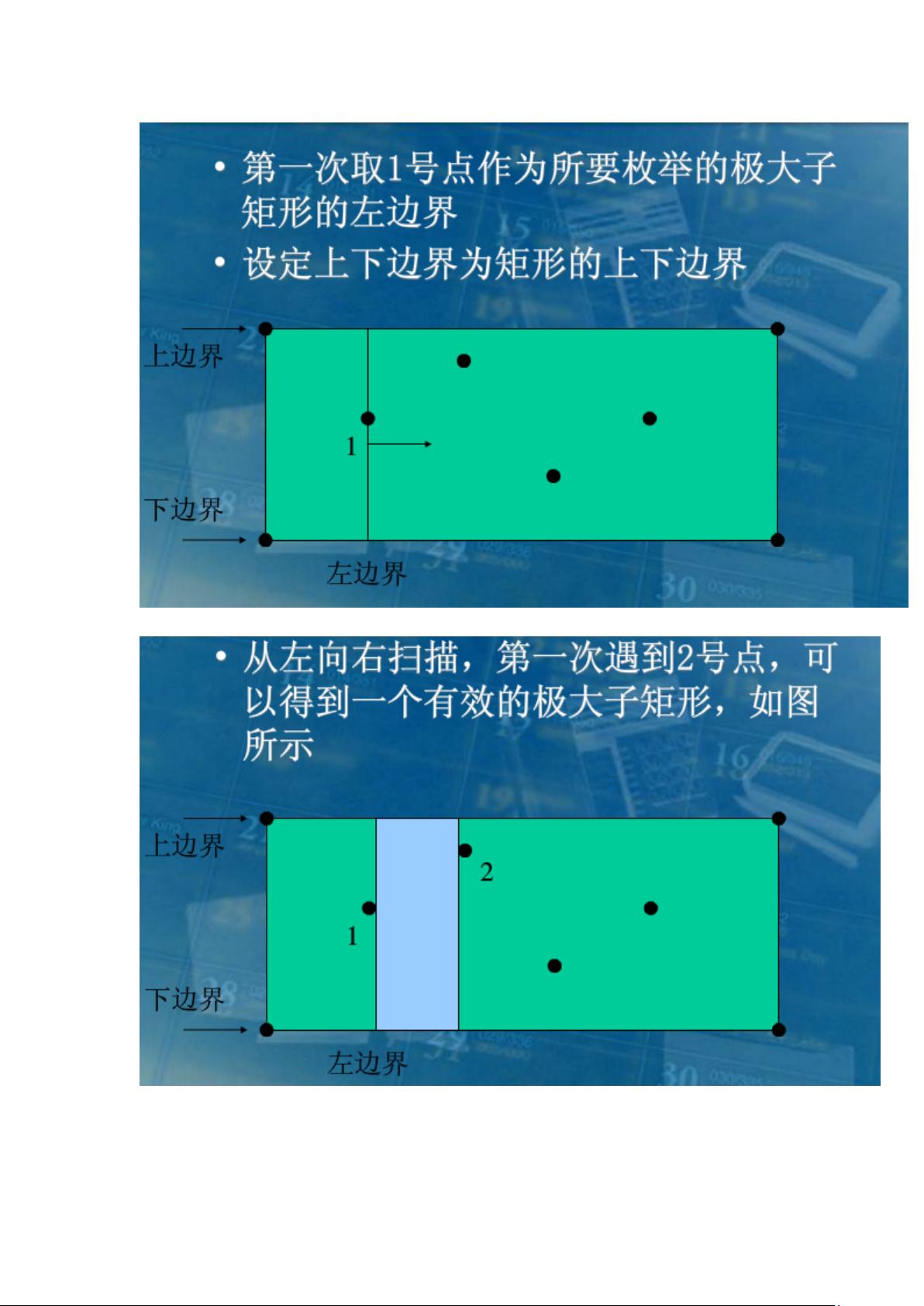
最大子矩阵指的是在一个矩阵中找到一个子矩阵，使得该子矩阵的元素之和最大。通常情况下，最大子矩阵问题可以通过动态规划或者分治算法来解决。找到最大子矩阵有助于解决一些实际问题，比如在图像处理中找到最大的连通区域等。 ### 最大子矩阵问题概述 #### 一、问题定义及应用场景 最大子矩阵问题是指在一个给定的矩阵中寻找一个子矩阵，使得该子矩阵内元素的和达到最大值。这种问题不仅在理论计算机科学中占有重要地位，而且在实际应用中也有广泛的应用场景，例如在图像处理领域用于识别图像中的特定区域，或者在数据分析中用于发现数据集中的异常模式。 #### 二、基本概念 - **有效子矩阵**：满足题目要求的子矩阵。 - **极大子矩阵**：满足题目要求且边界无法进一步扩大的子矩阵。 - **最大子矩阵**：在所有极大子矩阵中，具有最大值的那个子矩阵。 #### 三、求解方法 最大子矩阵问题可以通过多种算法解决，包括但不限于动态规划、分治算法等。 ### 极大化思想 求解最大子矩阵的核心思想在于极大化。简单来说，就是通过枚举所有可能的极大子矩阵，从中找出具有最大值的那个。 #### 四、如何求解极大子矩阵 在实际求解过程中，通常有两种方法： 1. **边界扩展法** - 这种方法的核心是从障碍点入手，不断尝试扩大子矩阵的边界。边界无法继续扩展的情况通常有两种： - 边界到达矩阵的边缘。 - 边界遇到另一个障碍点。 - 为了高效地实现这一点，我们可以按照障碍点的位置进行排序，并逐一考虑这些障碍点。在扩展边界的同时，还需要维护边界的有效性。 2. **动态规划** - 动态规划是一种非常强大的工具，适用于许多类型的最大子矩阵问题。 - 通过构建状态转移方程，动态规划能够有效地解决这类问题。关键在于正确定义状态以及找到合适的状态转移路径。 #### 五、示例分析 以下是一个具体的例子来帮助理解最大子矩阵问题的求解过程： ##### 示例题目：P1578 奶牛浴场 - **题目描述**：John 在牛场中想要建造一个浴场，但为了避免影响奶牛的产奶量，浴场不能覆盖任何产奶点。任务是找到最大面积的浴场，同时保证浴场不覆盖产奶点。 - **解决方案**： 1. **预处理**：将所有产奶点按照列坐标进行排序。 2. **枚举障碍点**：依次枚举每一个产奶点，将其视为浴场的左边界。 3. **扩展边界**：在此基础上，逐步扩展浴场的右边界，并保持边界的有效性。这意味着在扩展过程中，需要时刻关注其他障碍点的位置，以确保浴场的合法性。 4. **计算最大值**：通过上述过程，可以枚举出所有可能的极大子矩阵，并从中选出最大值。 #### 六、总结 最大子矩阵问题是一个典型的算法问题，涉及到了动态规划、分治等多种算法思想。通过合理的数据结构设计和高效的算法实现，可以在较短的时间内求解出问题的答案。在实际应用中，最大子矩阵问题的解决对于提高效率、优化资源分配等方面都有着重要的意义。