没有合适的资源?快使用搜索试试~ 我知道了~
资源推荐
资源详情
资源评论
第四章 信号的小波变换与分析
21/8/5

主要内容
小波变换
连续小波变换
离散小波变换与多分辨率分析
离散小波变换的应用

小波变换的概念是由法国从事石油信号处理的工程师
在 年首先提出的,通过物理的直观和信号处理的实际需要经验
的建立了反演公式,当时未能得到数学家的认可。正如 年法国
的热学工程师 提出任一函数都能展开成三角函数的无
穷级数的创新概念未能得到著名数学家 ,
以及 的认可一样。幸运的是,早在七十年代,
表示定理的发现、 空间的原子分解和无条件基的深入研
究为小波变换的诞生做了理论上的准备,而且 !" 还构造
了历史上非常类似於现在的小波基; # 年著名数学家 $ 偶
然构造出一个真正的小波基,并与 合作建立了构造小波基
的统一方法及其多尺度分析之后,小波分析才开始蓬勃发展起来,
其中比利时女数学家 %&"'( 撰写的《小波十讲 )*+(+
+,-(. 》对小波的普及起了重要的推动作用。它与 变换、
视窗 变换( /" 变换)相比,这是一个时间和频率的局网
域变换,因而能有效的从信号中提取资讯,通过伸缩和平移等运算
功能对函数或信号进行多尺度细化分析( (0(( ),解
决了 变换不能解决的许多困难问题,从而小波变化被誉为
“数学显微镜”,它是调和分析发展史上里程碑式的进展。

小波分析是当前应用数学和工程学科中一个迅速发展的
新领域,经过近 10 年的探索研究,重要的数学形式化体系已
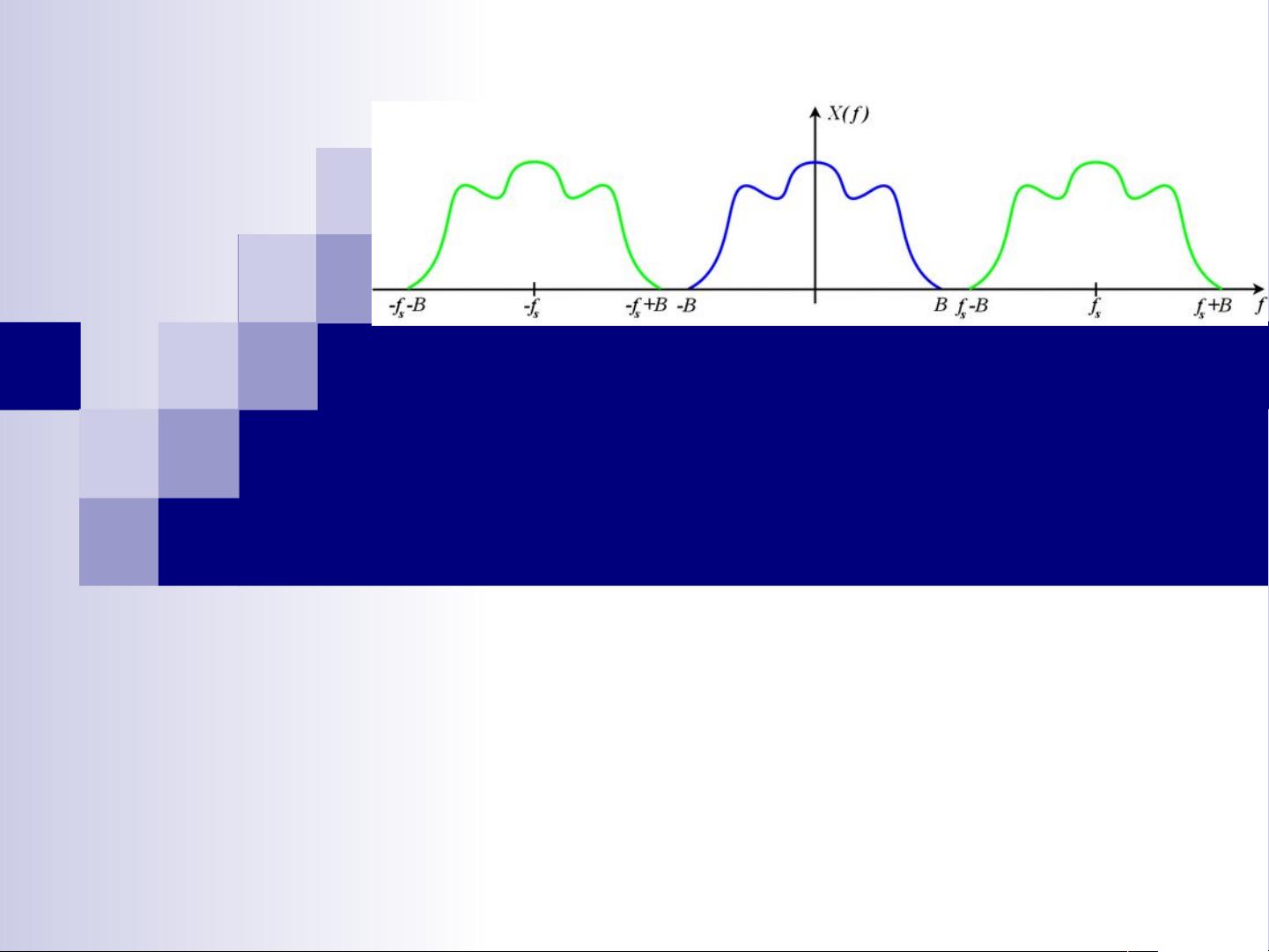
经建立,理论基础更加扎实。与 Fourier 变换相比,小波变换
是空间 ( 时间 ) 和频率的局部变换,因而能有效地从信号中提
取信息。通过伸缩和平移等运算功能可对函数或信号进行多尺
度的细化分析,解决了 Fourier 变换不能解决的许多困难问题。
小波变换联系了应用数学、物理学、计算机科学、信号与信息
处理、图像处理、地震勘探等多个学科。数学家认为,小波分
析是一个新的数学分支,它是泛函分析、 Fourier 分析、样调
分析、数值分析的完美结晶;信号和信息处理专家认为,小波
分析是时间—尺度分析和多分辨分析的一种新技术,它在信号
分析、语音合成、图像识别、计算机视觉、数据压缩、地震勘
探、大气与海洋波分析等方面的研究都取得了有科学意义和应
用价值的成果。

小波 (Wavelet) 这一术语,顾名思义,“小波”就是小的波形。
所谓“小”是指它具有衰减性;而称之为“波”则是指它的波动
性,其振幅正负相间的震荡形式。与 Fourier 变换相比,
小波变换是时间 ( 空间 ) 频率的局部化分析,它通过伸缩
平移运算对信号 ( 函数 ) 逐步进行多尺度细化,最终达到
高频处时间细分,低频处频率细分,能自动适应时频信号
分析的要求,从而可聚焦到信号的任意细节,解决了 Fouri
er 变换的困难问题,成为继 Fourier 变换以来在科学方法
上的重大突破。有人把小波变换称为“数学显微镜”。
主要适应突变信号和非平稳信号
剩余30页未读,继续阅读
资源评论

fjjoljh
- 粉丝: 0
- 资源: 5
上传资源 快速赚钱
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
资源上传下载、课程学习等过程中有任何疑问或建议,欢迎提出宝贵意见哦~我们会及时处理!
点击此处反馈



安全验证
文档复制为VIP权益,开通VIP直接复制
 信息提交成功
信息提交成功