PIPE v2.5: A Petri Net Tool for Performance Modelling [PDF]

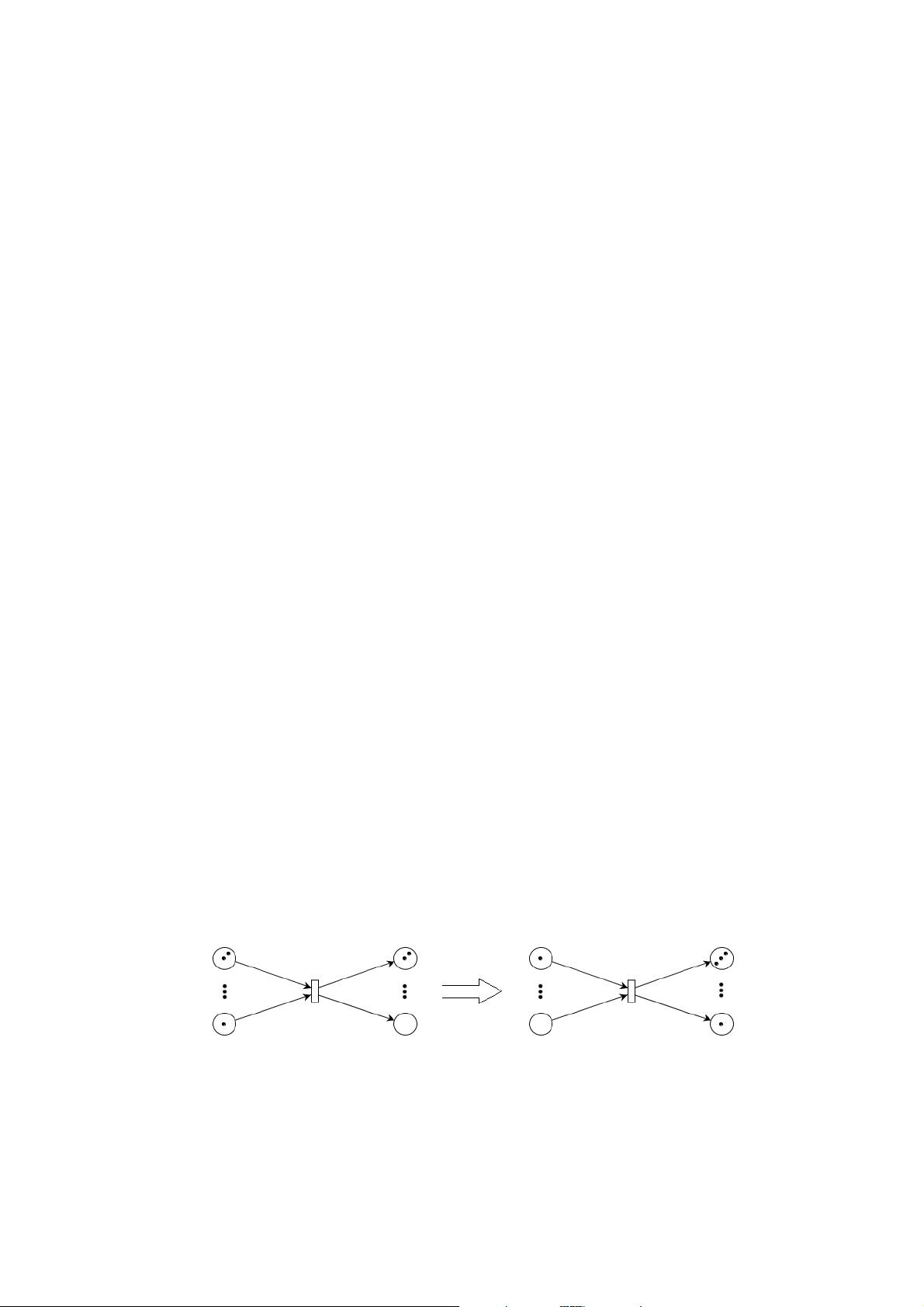
标题与描述概述的知识点： 1. **PIPE v2.5：** 一款广泛认可的、免费的、开源的、跨平台的Petri网建模工具，用于性能建模。 2. **Petri网理论：** Petri网是一种数学模型，用于描述并行系统的行为，特别是在计算机科学领域，用于建模和分析复杂系统的正确性和性能特性。 3. **性能建模与分析：** PIPE v2.5提供了一系列工具和功能，使用户能够对系统进行建模，并分析其性能指标，如响应时间、吞吐量等。 4. **抑制弧（Inhibitor Arcs）：** 抑制弧是Petri网中的一个特殊概念，允许在特定条件下阻止转换的发生，从而增加模型的灵活性和表达力。 5. **生成吸管（Siphons）和陷阱（Traps）：** 这些是Petri网分析中常用的概念，用于识别模型中的稳定状态或死锁情况，帮助分析人员理解系统的动态行为。 6. **界面改进与展示优化：** PIPE v2.5在用户界面和模型展示方面进行了改进，提供了更好的用户体验和更清晰的模型可视化。 详细说明： **PIPE v2.5** 是由西班牙巴利阿里群岛大学和英国帝国理工学院合作开发的一款高性能Petri网建模工具，旨在为用户提供一套全面的系统建模与性能分析解决方案。这款工具不仅适用于学术研究，也广泛应用于工业界，尤其在通信网络、制造系统、生物信息学等领域，因其强大的功能和开放性而受到青睐。 **Petri网理论** 提供了一种直观的图形化表示方法，通过“地方”（Places）和“转换”（Transitions）来描述系统的状态变化和事件触发，从而使得复杂的系统行为变得易于理解和分析。Petri网的灵活性使其能够适应各种不同的应用领域，从软件工程到生物系统模拟，都有着广泛的应用。 **性能建模与分析** 在PIPE v2.5中得到了进一步加强。该工具引入了抑制弧这一新特性，极大地提升了模型的表达能力。抑制弧允许模型设计者在某些条件下限制转换的触发，这种机制对于模拟具有条件约束的系统特别有用，例如，在一个生产线上，可能需要在特定条件下暂停某些操作，以确保资源的有效利用或避免冲突。 此外，PIPE v2.5还新增了一个分析模块，专门用于生成吸管和陷阱。吸管是指在Petri网中能够消耗所有标记的集合，而陷阱则是指一旦有标记进入就无法再离开的集合。这些概念对于检测模型中的潜在问题，如死锁或资源耗尽，具有重要意义。通过对模型进行深入分析，可以提前识别出可能的性能瓶颈或系统故障点，从而指导设计者优化系统结构。 在用户界面和展示方面，PIPE v2.5也做出了显著改进。新的界面设计更加人性化，使用户能够更直观地创建和编辑Petri网模型。同时，模型的展示效果得到了提升，使得即使是复杂的模型也能够清晰地呈现出来，便于分析和交流。这些改进不仅提高了工作效率，也增强了团队之间的协作，尤其是在远程工作环境下，清晰的模型展示尤为重要。 **PIPE v2.5** 作为一款先进的Petri网建模工具，通过引入抑制弧、增强分析功能以及优化用户界面，为系统性能建模与分析提供了强大的支持。无论是科研工作者还是工业界的专业人士，都能够从中受益，利用它来解决实际问题，推动技术创新与发展。