用光谱注意重新思考图形变换器_RethinkingGraphTransformerswithSpectralAtten资源-CSDN文库

版权申诉

142 浏览量 2022-02-05 09:22:37 上传评论收藏 1.74MB PDF 举报

近年来，Transformer架构在序列处理领域取得了显著的成功，但将其应用到其他数据结构，如图，一直受到如何正确定义位置的限制。这篇论文“Rethinking Graph Transformers with Spectral Attention”提出了光谱注意力网络（Spectral Attention Network, SAN），它利用学习到的位置编码（Learned Positional Encoding, LPE）来利用拉普拉斯矩阵的完整谱，从而学习图中每个节点的位置。这种LPE随后添加到图的节点特征中，并传递给全连接的Transformer。在传统的图神经网络（GNNs）中，通常通过稀疏的消息传递过程直接编码图结构。这种方法中，向量消息在图中相连的节点间迭代传递。尽管这种方法有多种实现形式，但它可能会导致信息瓶颈问题，即“过度压缩”（over-squashing），这限制了模型对复杂图结构的表示能力。为了解决这个问题，论文提出的SAN利用拉普拉斯矩阵的完整谱，理论上增强了模型区分不同图的能力，并能更好地检测相似子结构之间的共振。通过完全连接图，Transformer避免了过度压缩问题，能够更好地模拟物理现象，如热传递和电相互作用。实验表明，当在四个标准数据集上进行测试时，该模型的表现与最先进的GNNs相当或更好，而且大幅度超越了基于注意力的模型，成为首个在图基准测试中表现优秀的全连接架构。 SAN的关键创新在于其学习的位置编码LPE，它不是静态定义的，而是根据图的拉普拉斯谱动态学习的。拉普拉斯谱包含了图的全局和局部信息，使得模型能够捕捉到图的拓扑特性。此外，全连接的Transformer层允许节点间的直接通信，无论它们在原始图中的距离多远，这增强了模型对长距离依赖的捕获能力。实验部分，论文对比了SAN与其他GNNs和基于注意力的模型在节点分类、图分类等任务上的性能，结果显示了SAN在多个指标上的优越性。此外，作者还分析了模型的复杂性和可扩展性，讨论了潜在的应用场景和未来的研究方向。这篇论文为图神经网络的发展提供了一个新的视角，通过引入光谱注意力，不仅解决了位置编码的问题，还提升了模型对图结构的理解和表示能力，为图数据处理提供了更强大的工具。这进一步推动了Transformer架构在图学习领域的应用，为相关研究开辟了新的可能性。

资源推荐

资源详情

资源评论

Rethinking Graph Transformers with Spectral

Attention

Devin Kreuzer

∗

McGill University, Mila

Montreal, Canada

devin.kreuzer@mail.mcgill.ca

Dominique Beaini

Valence Discovery

Montreal, Canada

dominique@valencediscovery.com

William L. Hamilton

McGill University, Mila

Montreal, Canada

wlh@cs.mcgill.ca

Vincent Létourneau

University of Ottawa

Ottawa, Canada

vletour2@uottawa.ca

Prudencio Tossou

Valence Discovery

Montreal, Canada

prudencio@valencediscovery.com

Abstract

In recent years, the Transformer architecture has proven to be very successful in

sequence processing, but its application to other data structures, such as graphs,

has remained limited due to the difﬁculty of properly deﬁning positions. Here, we

present the Spectral Attention Network (SAN), which uses a learned positional

encoding (LPE) that can take advantage of the full Laplacian spectrum to learn the

position of each node in a given graph. This LPE is then added to the node features

of the graph and passed to a fully-connected Transformer. By leveraging the full

spectrum of the Laplacian, our model is theoretically powerful in distinguishing

graphs, and can better detect similar sub-structures from their resonance. Further,

by fully connecting the graph, the Transformer does not suffer from over-squashing,

an information bottleneck of most GNNs, and enables better modeling of physical

phenomenons such as heat transfer and electric interaction. When tested empirically

on a set of 4 standard datasets, our model performs on par or better than state-of-the-

art GNNs, and outperforms any attention-based model by a wide margin, becoming

the ﬁrst fully-connected architecture to perform well on graph benchmarks.

1 Introduction

The prevailing strategy for graph neural networks (GNNs) has been to directly encode graph structure

structure through a sparse message-passing process [

]. In this approach, vector messages

are iteratively passed between nodes that are connected in the graph. Multiple instantiations of

this message-passing paradigm have been proposed, differing in the architectural details of the

message-passing apparatus (see [19] for a review).

However, there is a growing recognition that the message-passing paradigm has inherent limitations.

The expressive power of message passing appears inexorably bounded by the Weisfeiler-Lehman iso-

morphism hierarchy [

]. Message-passing GNNs are known to suffer from pathologies, such

∗

Equal contribution.

35th Conference on Neural Information Processing Systems (NeurIPS 2021).

arXiv:2106.03893v3 [cs.LG] 27 Oct 2021

as oversmoothing, due to their repeated aggregation of local information [

], and over-squashing,

due to the exponential blow-up in computation paths as the model depth increases [1].

As a result, there is a growing interest in deep learning techniques that encode graph structure as a soft

inductive bias, rather than as a hard-coded aspect of message passing [

]. A central issue with

message-passing paradigm is that input graph structure is encoded by restricting the structure of the

model’s computation graph, inherently limiting its ﬂexibility. This reminds us of how early recurrent

neural networks (RNNs) encoded sequential structure via their computation graph—a strategy that

leads to well-known pathologies such as the inability to model long-range dependencies [20].

There is a growing trend across deep learning towards more ﬂexible architectures, which avoid strict

and structural inductive biases. Most notably, the exceptionally successful Transformer architecture

removes any structural inductive bias by encoding the structure via soft inductive biases, such as

positional encodings [

]. In the context of GNNs, the self-attention mechanism of a Transformer

can be viewed as passing messages between all nodes, regardless of the input graph connectivity.

Prior work has proposed to use attention in GNNs in different ways. First, the GAT model [

]

proposed local attention on pairs of nodes that allows a learnable convolutional kernel. The GTN work

[

] has improved on the GAT for node and link predictions while keeping a similar architecture,

while other message-passing approaches have used enhancing spectral features [

] . More

recently, the GT model [

] was proposed as a generalization of Transformers to graphs, where they

experimented with sparse and full graph attention while providing low-frequency eigenvectors of the

Laplacian as positional encodings.

In this work, we offer a principled investigation of how Transformer architectures can be applied

in graph representation learning.

Our primary contribution

is the development of novel and

powerful learnable positional encoding methods, which are rooted in spectral graph theory. Our

positional encoding technique — and the resulting spectral attention network (SAN) architecture —

addresses key theoretical limitations in prior graph Transformer work [

] and provably exceeds the

expressive power of standard message-passing GNNs. We show that full Transformer-style attention

provides consistent empirical gains compared to an equivalent sparse message-passing model, and

we demonstrate that our SAN architecture is competitive with or exceeding the state-of-the-art on

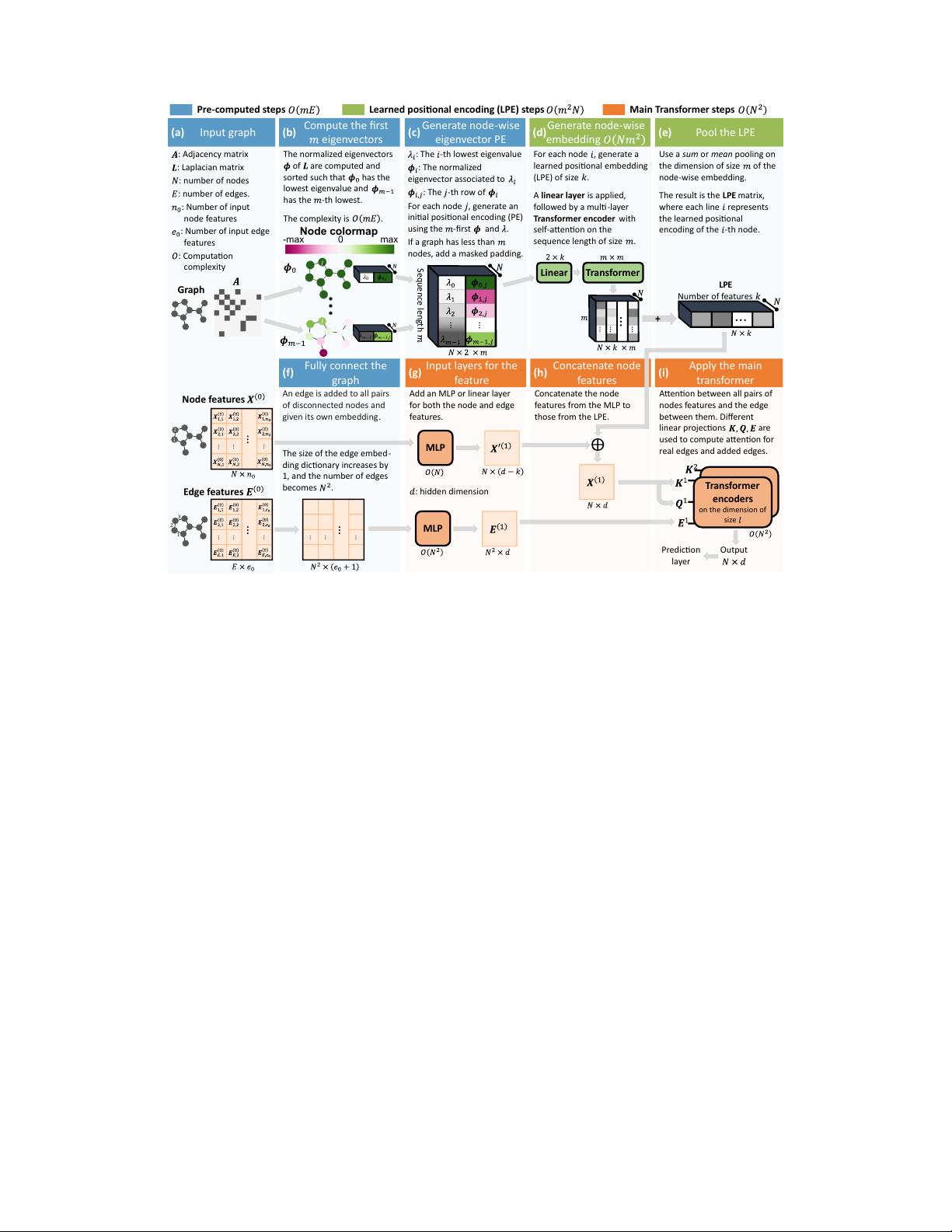
several well-known graph benchmarks. An overview of the entire method is presented in Figure 1,

with a link to the code here: https://github.com/DevinKreuzer/SAN.

2 Theoretical Motivations

There can be a signiﬁcant loss in structural information if naively generalizing Transformers to graphs.

To preserve this information as well as local connectivity, previous studies [

] have proposed to

use the eigenfunctions of their Laplacian as positional encodings. Taking this idea further by using

the full expressivity of eigenfunctions as positional encodings, we can propose a principled way

of understanding graph structures using their spectra. The advantages of our methods compared to

previous studies [37, 14] are shown in Table 1.

Table 1: Comparison of the properties of different graph Transformer models.

MODELS GAT [37] GT sparse [14] GT full [14] SAN (Node LPE)

Preserves local structure in attention 3 3 7 3

Uses edge features 7 3 7 3

Connects non-neighbouring nodes 7 7 3 3

Uses eigenvector-based PE for attention 7 3 3 3

Use a PE with structural information 7 3 7

Considers the ordering of the eigenvalues 7 3 3 3

Invariant to the norm of the eigenvector - 3 3 3

Considers the spectrum of eigenvalues 7 7 7 3

Considers variable # of eigenvectors - 7 7 3

Aware of eigenvalue multiplicities - 7 7 3

Invariant to the sign of the eigenvectors - 7 7 7

Presented results add full connectivity before computing the eigenvectors, thus losing the structural informa-

tion of the graph.

Node features

: Adjacency matrix

: Laplacian matrix

: number of nodes

: number of edges.

: Number of input

node features

: Number of input edge

features

: Computaon

complexity

(a)

Pre-computed steps Learned posi�onal encoding (LPE) steps

max0-max

Node colormap

Input graph

The normalized eigenvectors

of are computed and

sorted such that has the

lowest eigenvalue and

has the -th lowest.

The complexity is .

(b)

Compute the rst

eigenvectors

(c)

Generate node-wise

eigenvector PE

: The -th lowest eigenvalue

: The normalized

eigenvector associated to

: The -th row of

For each node , generate an

inial posional encoding (PE)

using the -rst and .

If a graph has less than

nodes, add a masked padding.

(d)

Generate node-wise

embedding

For each node , generate a

learned posional embedding

(LPE) of size .

A linear layer is applied,

followed by a mul-layer

Transformer encoder with

self-aenon on the

sequence length of size

Sequence length

(e) Pool the LPE

Use a sum or mean pooling on

the dimension of size of the

node-wise embedding.

The result is the LPE matrix,

where each line

represents

the learned posional

encoding of the -th node.

LPE

Number of features

Main Transformer steps

Graph

⋮⋮ ⋮

Edge features

⋮⋮ ⋮

(f)

Fully connect the

graph

An edge is added to all pairs

of disconnected nodes and

given its own embedding.

The size of the edge embed-

ding diconary increases by

1, and the number of edges

becomes

Add an MLP or linear layer

for both the node and edge

features.

(g)

Input layers for the

feature

⋮⋮ ⋮

Concatenate the node

features from the MLP to

those from the LPE.

(h)

Concatenate node

features

Aenon between all pairs of

nodes features and the edge

between them. Dierent

linear projecons

are

used to compute aenon for

real edges and added edges.

(i)

Apply the main

transformer

OutputPredicon

layer

MLP

Transformer

encoders

on the dimension of

size

𝑗

𝝓

𝑚−1,𝑗

𝜆

𝑚−1

𝝓

0,𝑗

𝜆

𝑗

Linear Transformer

: hidden dimension

Figure 1: The proposed SAN model with the node LPE, a generalization of Transformers to graphs.

2.1 Absolute and relative positional encoding with eigenfunctions

The notion of positional encodings (PEs) in graphs is not a trivial concept, as there exists no canonical

way of ordering nodes or deﬁning axes. In this section, we investigate how eigenfunctions of the

Laplacian can be used to deﬁne absolute and relative PEs in graphs, to measure physical interactions

between nodes, and to enable ”hearing” of speciﬁc sub-structures - similar to how the sound of a

drum can reveal its structure.

2.1.1 Eigenvectors equate to sine functions over graphs

In the Transformer architecture, a fundamental aspect is the use of sine and cosine functions as PEs

for sequences [36]. However, sinusoids cannot be clearly deﬁned for arbitrary graphs, since there is

no clear notion of position along an axis. Instead, their equivalent is given by the eigenvectors

the graph Laplacian

. Indeed, in a Euclidean space, the Laplacian (or Laplace) operator corresponds

to the divergence of the gradient and its eigenfunctions are sine/cosine functions, with the squared

frequencies corresponding to the eigenvalues (we sometimes interchange the two notions from here

on). Hence, in the graph domain, the eigenvectors of the graph Laplacian are the natural equivalent of

sine functions, and this intuition was employed in multiple recent works which use the eigenvectors

as PEs for GNNs [15], for directional ﬂows [4] and for Transformers [14].

Being equivalent to sine functions, we naturally ﬁnd that the Fourier Transform of a function

F [f]

applied to a graph gives

F [f](λ

) = hf, φ

, where the eigenvalue is considered as a position in the

Fourier domain of that graph [

]. Thus, the eigenvectors are best viewed as vectors positioned on the

axis of eigenvalues rather than components of a matrix as illustrated in Figure 2.

2.1.2 What do eigenfunctions tell us about relative positions?

In addition to being the analog of sine functions, the eigenvectors of the Laplacian also hold important

information about the physics of a system and can reveal distance metrics. This is not surprising as

剩余17页未读，继续阅读

评论收藏

内容反馈

版权申诉

易小侠

粉丝: 6596
资源: 9万+

用光谱注意重新思考图形变换器_Rethinking Graph Transformers with Spectral Atten

最新资源

用光谱注意重新思考图形变换器_Rethinking Graph Transformers with Spectral Atten

重新思考位置编码_Rethinking Positional Encoding

藏经阁-NO MORE _SBT ASSEMBLY__RETHINKING SPARK-SUBMIT USING CUESHEE

重新思考具有改进内存覆盖率的时空网络以实现高效视频对象分割_Rethinking Space-Time Networks wit

重新思考解决联邦学习中数据异构性的体系结构设计_Rethinking Architecture Design for Tackl

重新思考CrowdsA纯基于点的框架中的计数和本地化_Rethinking Counting and Localization

重新思考集成传感和通信识别精度与通信速率之间的权衡_Rethinking the Tradeoff in Integrated

信息安全_数据安全_Rethinking_Access_Control_and_Au.pdf

重新思考关键点表示法将关键点和姿势建模为多人姿势估计的对象_Rethinking Keypoint Representation

信息安全_数据安全_law-f03_rethinking_employee_surv.pdf

重新思考用于恢复旋转和鱼眼畸变的深单像相机校准的通用相机模型_Rethinking Generic Camera Models

从自顶向下的角度重新思考视频对象分割中的跨模式交互_Rethinking Cross-modal Interaction fro

Statistical_rethinking-

Shuffle Transformer重新思考视觉转换器的空间洗牌_Shuffle Transformer Rethinking

stat_rethinking_2020:20202021年冬季统计反思课程

stats_rethinking_julia

Statistics_Rethinking_with_brms_ggplot2_and_the_tidyverse_2_ed：书本版本位于此处：

Statistical_Rethinking_Exercices:Jupyter笔记本使用Python库练习统计数据

Statistical_Rethinking_with_brms_ggplot2_and_the_tidyverse:书本版本住在这里

Cobalt Strike下载

北京邮电大学计算机考研复试笔试资料

计算机系统-笔记-HUN2021级

cs1.6老版本供下载

合成孔径雷达的经典成像算法cs(matlab)仿真代码（吐血整理，内容全，注释全）

港大CS（MSC）面试整理

合成孔径雷达RD CS OmegaK算法点目标仿真.rar

计算机科学导论原书第二版答案.zip

Cobalt-Strike-4.5

cobaltstrike4.3.zip

最新资源