支持向量机应用及MATLAB

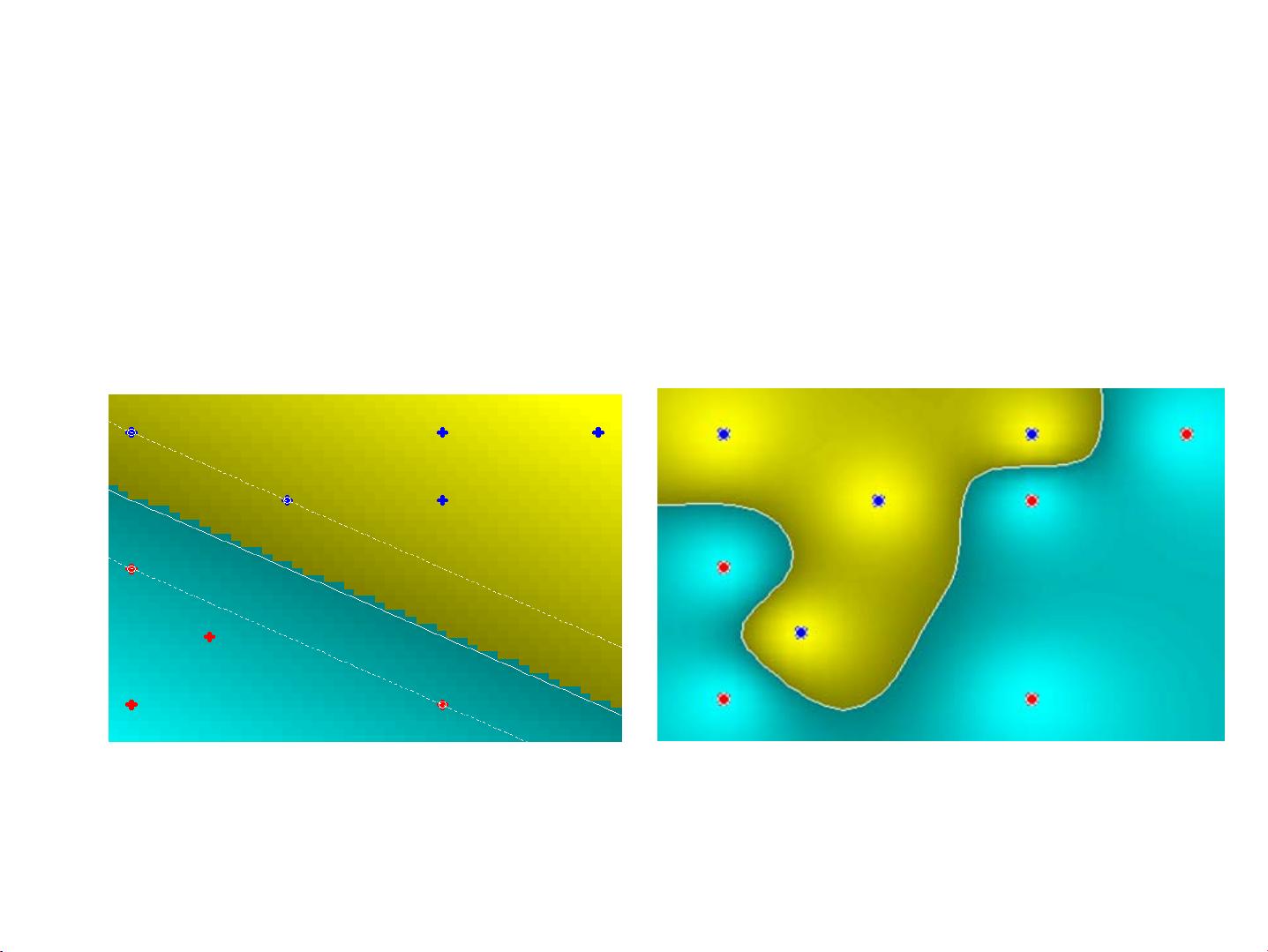
### 支持向量机应用及MATLAB #### 一、引言与基础知识 ##### 1.1 支持向量机(Support Vector Machine, SVM) 支持向量机是一种广泛应用于机器学习领域的算法，主要用于分类和回归分析。其基本思想是在特征空间中找到一个最优的超平面（对于二维空间中的数据点，这个超平面就是一条直线），使得正负两类样本被正确地分割开，并且这两类样本到超平面的平均距离最大。这一过程确保了分类器的泛化能力，即使其在未见过的数据上也能有较好的表现。 ##### 1.2 相关参考资料 - **《统计学习理论的本质》**：Vladimir N. Vapnik 著，张学工译，清华大学出版社，2000.09 - **《支持向量机导论》**：N. Cristianini, J. Shawe-Taylor 著，电子工业出版社，2004.03 - **《Support Vector Classification》**：Steven Gunn - **在线资源**：www.kernel-machines.org、www.support-vector.net - **其他资源**：Bernhard Scholkopf, Alex J. Smola, Christopher J. C. Burges #### 二、支持向量机的应用 ##### 2.1 手写体数字识别 - **应用背景**：支持向量机在手写体数字识别领域有着卓越的表现。例如，NIST手写体数字数据库的前100个样本，使用多项式支持向量机可以达到低于0.8%的错误率。 - **方法对比**：与LeNet4等深度学习模型相比，支持向量机在此类任务上的表现也非常优秀，尽管深度学习模型可能在更复杂的数据集上具有优势。 ##### 2.2 性别识别 支持向量机同样适用于基于图像或其他生物特征的性别识别任务。通过构建有效的特征表示和支持向量机模型，可以实现高准确性的性别分类。 #### 三、支持向量机的原理 ##### 3.1 为何支持向量机有如此好的性能？ 支持向量机之所以能够取得优秀的性能，主要得益于以下几点： - **最大化边界**：支持向量机试图寻找一个能够最大化边界（margin）的分类超平面，这样可以提高模型的鲁棒性和泛化能力。 - **核技巧**：支持向量机通过使用核技巧（Kernel Trick），能够在非线性可分的情况下依然有效地找到分类边界。 - **稳健性**：支持向量机对异常值不太敏感，这使得它在处理含有噪声的数据时更加稳健。 ##### 3.2 何为最优分类面？ 在支持向量机中，最优分类面是指那些能够最大程度地区分不同类别样本的超平面。具体来说，这个超平面应该满足两个条件： - 尽可能多地将正负样本区分开来。 - 在保持分类正确的前提下，最大化边界的宽度。 #### 四、支持向量机的数学模型 支持向量机的数学模型主要包括以下几个部分： 1. **模型定义**：假设训练样本集为\(\{(x_1, y_1), (x_2, y_2), \ldots, (x_l, y_l)\}\)，其中\(x_i\)为输入向量，\(y_i \in \{-1, +1\}\)为对应的类别标签。支持向量机的目标是找到一个分类面\(g(x) = w^Tx + b\)，使得对于所有的训练样本，都满足\(y_i(g(x_i)) \geq 1\)。 2. **优化目标**：为了找到最优分类面，我们需要最小化\(w\)的范数\(\frac{1}{2}||w||^2\)，同时满足上述约束条件。 3. **拉格朗日对偶法**：通过构造拉格朗日函数\(L(w, b, \alpha)\)并求解其鞍点，可以将原问题转化为一个关于拉格朗日乘子\(\alpha_i\)的对偶问题。具体步骤包括： - 构造拉格朗日函数\(L(w, b, \alpha)\)。 - 对\(L(w, b, \alpha)\)关于\(w\)和\(b\)求偏导，并令偏导数等于0，从而得到\(w\)和\(b\)的表达式。 - 代入拉格朗日函数中，得到关于\(\alpha_i\)的对偶问题。 通过以上步骤，我们可以利用MATLAB等工具实现支持向量机算法，并将其应用于实际问题中。 #### 五、结论 支持向量机作为一种强大的机器学习算法，在多种应用场景中都展现出了优异的表现。无论是手写体数字识别还是性别识别，支持向量机都能够提供高效的解决方案。通过理解支持向量机的基本原理和数学模型，我们可以更好地利用这一工具解决实际问题。