
IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 28, NO. 11, NOV. 2006 2
and discrete potential theory, one may calculate the probability,
x
s
i
, that a random walker starting at pixel v
i
first reaches
a seed with label s, by solving the circuit theory problem
that corresponds to a combinatorial analog of the Dirichlet
problem [5]. Ground (i.e., fix the potential to zero) all seed
points belonging to labels other than s and establish a unit
voltage source with ground that fixes the s-labeled seeds to
have a unit potential. The electric potentials established at
each unseeded node provide the probabilities that a walker
originating from that node will first reach the seed with label
s. These electric potentials may be calculated through the
solution of a system of sparse linear equations, as described in
section III-G. The full K-tuple may be calculated by finding
the potentials established through switching “on” (providing
a unit voltage source to) each labeled collection of nodes
and “off” (grounding) the remaining labeled nodes. Therefore,
K −1 systems of linear equations must be solved. By linearity
(i.e., the principle of superposition in circuit theory), the
potentials so calculated must sum to unity. This allows us to
avoid solving for one of the systems by subtracting the sum
of the calculated potentials from unity to find the last entry in
the full K-tuple. A function that solves the Dirichlet problem
for a given set of boundary conditions is known as harmonic.
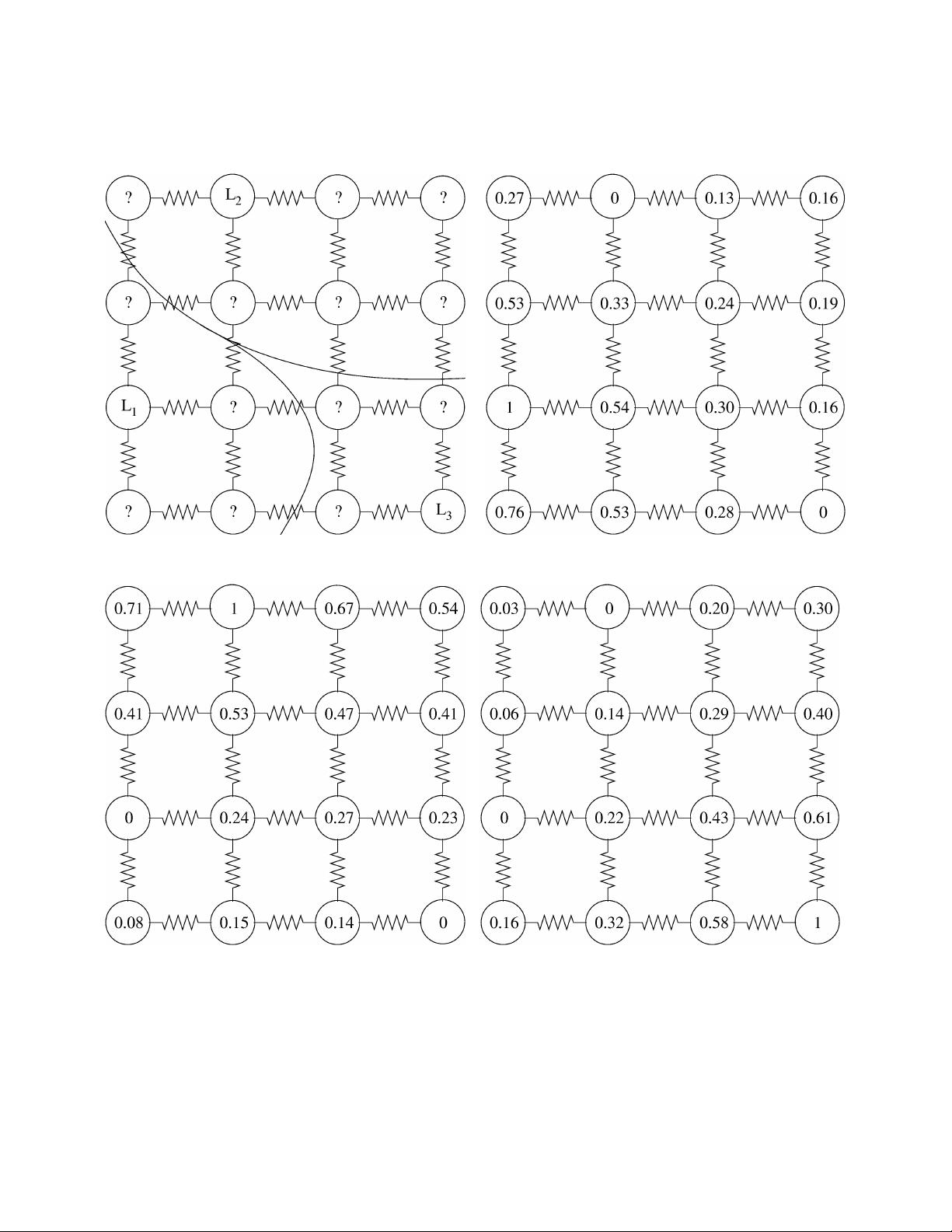
Figure I illustrates the harmonic functions (and subsequent
segmentation) obtained for a 4 × 4 graph with unit weights in
the presence of three seeds with different labels.
Additional properties of our approach that will be estab-
lished in Section IV-C include:
1) Each segment is guaranteed to be connected to seed
points with the same label, i.e., there are no isolated
regions of a particular label that contain no seed points.
2) The K-tuple of probabilities at each pixel is equal to the
weighted average of the K-tuples of neighboring pixels,
with the weights given by walker biases.
3) The solution for the potentials is unique.
4) The expected segmentation for an image of pure noise,
given by independent, equal-mean, random variables, is
equal to that obtained in the neutral segmentation.
A rich tradition of work in image segmentation has focused
on the establishment of appropriate image (object) models
and the development of algorithms focused on finding the
parameters for these models (e.g., [11]). For example, the
FRAME model of [12] provides a method for both synthesis
and analysis of image textures. A different line of research
in computer vision has first established the desired behavior
of an algorithm and then set out to identify a PDE or other
physical process that exhibits the desired behavior. In such
approaches, an image is typically viewed as a domain with
material properties (metric) induced by the image content upon
which the PDE or other physical process is simulated. Notable
examples of research along this second line of work include
anisotropic diffusion for image filtering [13] and normalized
cuts for image segmentation [14]. In such approaches, the
primary focus is typically on the characteristic behavior of
the process and the manner in which the image content
induces a metric is left as a task-specific question (e.g.,
this information may come from intensity gradients, color
gradients or texture gradients, as appropriate to the particular
problem). The present random walker approach follows from
this second tradition in computer vision in which desirable
behavioral properties of an interactive segmentation algorithm
are identified and a particular physical process is proposed
that exhibits the required characteristics. In this case, the
characteristics that we try to capture in an interactive seg-
mentation algorithm are: 1) Location of weak (or missing)
boundaries, 2) Noise robustness, 3) Ability to identify multiple
objects simultaneously, 4) Fast computation (and editing), 5)
Avoidance of small/trivial solutions (i.e., an avoidance of a
“small cut” phenomenon).
This paper is organized as follows. Section II reviews the
relationship of this work to previous approaches. Section III
gives a simple weighting function, derives the set of linear
equations that must be solved and provides implementation de-
tails. Section IV establishes theoretical properties and Section
V examines behavioral properties of the algorithm. Section VI
provides segmentation results and we conclude in Section VII
with a summary of the algorithm presented and a discussion
of future work.
II. PRIOR WORK
Image segmentation is a vast topic. Therefore, we limit
our review to supervised and/or graph-based algorithms. Ad-
ditional work on random walks and combinatorial harmonic
functions will also be discussed.
A. Supervised segmentation
Supervised segmentation algorithms typically operate under
one of two paradigms for guidance: 1) Specification of pieces
of the boundary of the desired object or a nearby complete
boundary that evolves to the desired boundary, 2) Specification
of a small set of pixels belonging to the desired object and
(possibly) a set of pixels belonging to the background. We
note also that any of the automatic segmentation algorithms
might be considered supervised by subsequent user selection
of the desired segment. However, if the desired object is
not a complete segment, a secondary clustering/segmentation
algorithm must be employed to split or merge the automatic
segments.
The intelligent scissors algorithm [15] treats the image as
a graph where each pixel is associated with a node and a
connectivity structure is imposed. This technique requires the
user to place points along the boundary of the desired object.
Dijkstra’s algorithm is then used to compute the shortest path
between the user-defined points and this path is treated as
the object boundary. The algorithm is simple to implement,
very fast and may be used to obtain an arbitrary boundary
with enough points. Unfortunately, a low-contrast or noisy
boundary may require the specification of many points and
the algorithm is inapplicable to 3D boundaries.
Although the family of active contours and level sets is
large [16], a user is generally asked to place a contour near
the desired boundary and the algorithm evolves the boundary
to a local energy minimum. Many different terms in the energy
functional may be used to achieve different effects or employ



 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助 
 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜

 信息提交成功
信息提交成功