### NOIP普及讲座5-树的基础知识(PASCAL)
#### 树的基本概念
**树的定义**
树是由n(n > 0)个结点构成的有穷集合,具有以下特性:
1. 存在一个特定的结点,称为根结点。
2. 剩余的结点可以划分为m(m ≥ 0)个互不相交的非空子集T1, T2, …, Tm,其中每一个都是树,并且称为根结点的子树。
**树的表示方法**
树可以通过以下两种方式进行表示:
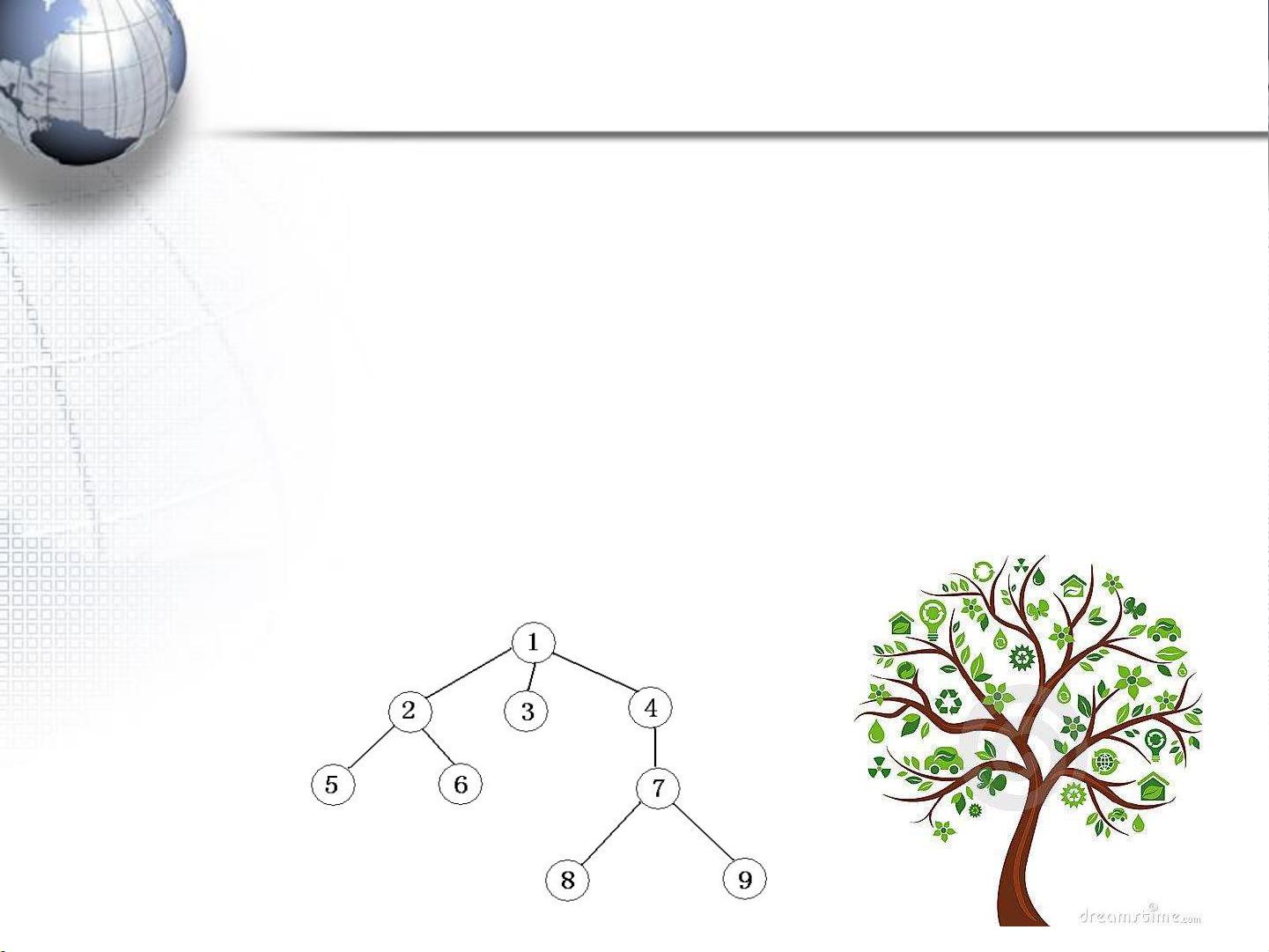
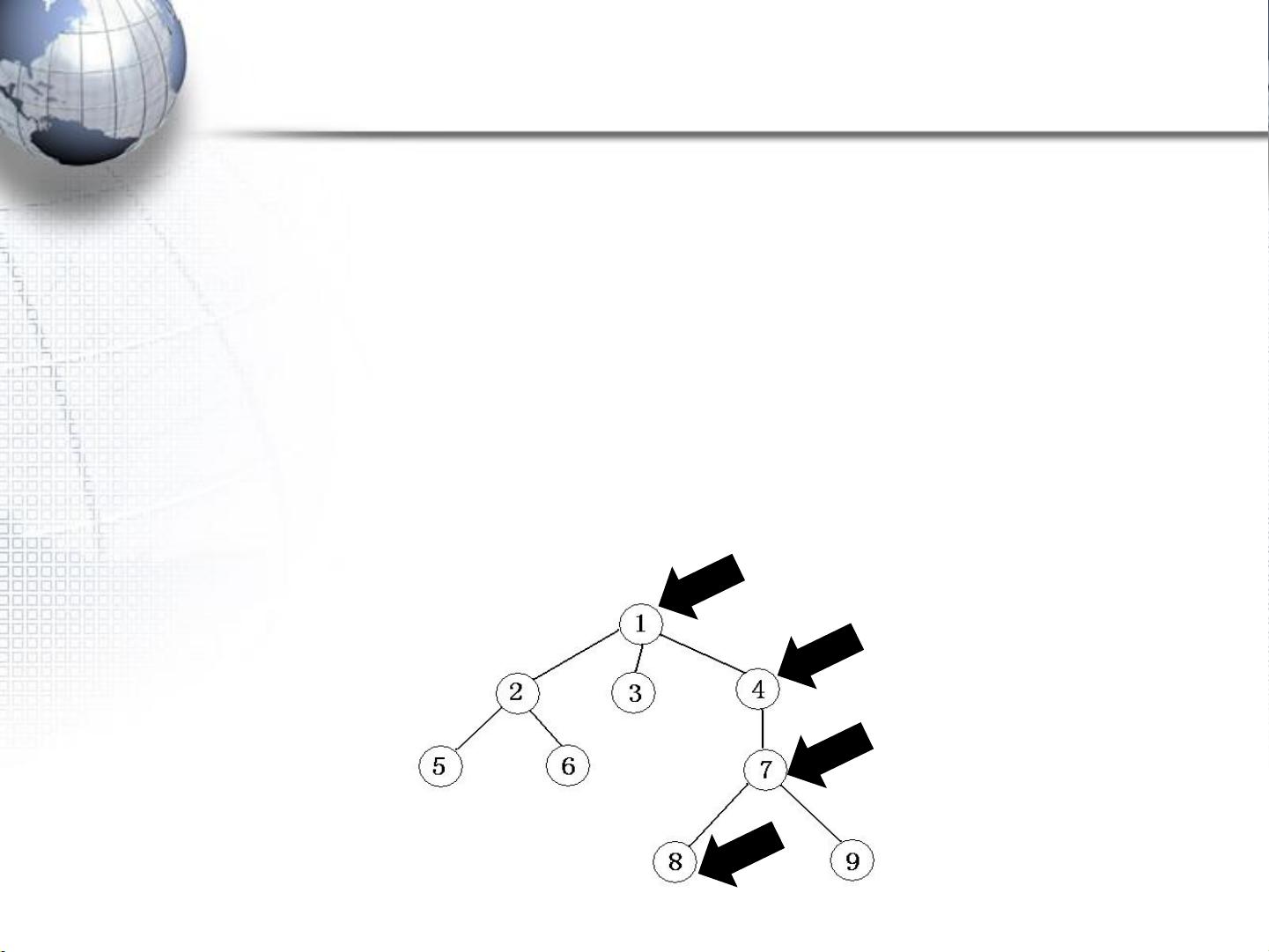
1. **图示表示**:通过图形来直观展示树的结构,结点用圆圈表示,连线表示父子关系。
2. **广义表表示**:利用广义表的形式来表示树的结构,例如:(1 (2 (5, 6), 3, 4 (7 (8, 9))))。
**树的基本术语**
1. **结点的度与树的度**:结点的度是指该结点拥有的子结点数量,而树的度则是所有结点度数中的最大值。
2. **分支结点与叶子结点**:度数大于0的结点被称为分支结点,度数为0的结点则被称为叶子结点。
3. **孩子结点、双亲结点与兄弟结点**:一个结点的子结点被称为该结点的孩子结点,相应地,孩子结点的父结点被称为该孩子的双亲结点。具有相同双亲结点的结点被称为兄弟结点。
4. **树的深度与宽度**:树的深度是指树中最远结点的距离根结点的最大距离,而树的宽度是指树中某一层的最大结点数。
#### 二叉树的基本知识
**二叉树的基本概念**
二叉树是一种特殊的树结构,每个结点最多有两个子结点,分别称为左子结点和右子结点。
**二叉树的性质**
1. **性质1**:二叉树的第i层至多有2^(i-1)个结点(i ≥ 1)。
2. **性质2**:深度为h的二叉树至多有2^h - 1个结点(h ≥ 1)。若一个二叉树的深度为k且恰好有2^k - 1个结点,则称该二叉树为满二叉树。
3. **性质3**:对于任意二叉树,其叶子结点的数量n0等于度为2的结点数量n2加1。
4. **性质4**:具有n个结点的完全二叉树的深度为trunc(log2(n)) + 1。完全二叉树的定义是深度为k的二叉树,如果有n个结点,那么它的结构与深度为k的满二叉树中编号为1到n的结点完全一致。
5. **性质5**:对于n个结点的完全二叉树,任一结点(编号为i)如果i = 1,则该结点为根结点,无父结点;若i > 1,则其父结点编号为trunc(i / 2)。同时,若2i > n,则结点i无左子结点,否则左子结点编号为2i;若2i + 1 > n,则结点i无右子结点,否则右子结点编号为2i + 1。
**二叉树的存储结构**
1. **顺序存储**:对于完全二叉树,可以将其结点按层序编号存入一维数组中,编号为i的结点存放在数组的第i个位置。
- **示例**:对于结点序列LDCPFEMHNL,按照层序编号可以得到数组存储形式为[L, D, C, P, F, M, E, H, N, L]。
2. **链式存储**:通过指针链接的方式存储二叉树结点,每个结点包含数据域和指向左右子结点的指针。
- **Pascal实现**:
```pascal
type node = record
data: char;
left, right: longint;
end;
var
a: array[1..n] of node;
```
- **C++实现**:
```c++
struct node {
char data;
int left, right;
};
node a[1001];
```
- **存储示例**:对于结点序列LDCPFEMHNL,采用链式存储方式,可以得到如下结构:
```
data: [L, D, C, P, F, M, E, H, N, L]
left: [2, 4, 0, 7, 0, 0, 0, 0, 0, 0]
right: [3, 5, 0, 8, 0, 0, 0, 0, 0, 0]
```
#### 二叉树的建立
**顺序存储**
通过字符串构建二叉树,使用特殊字符标识空结点,如“###”表示空结点。
- **示例**:“LDPCFM###EH#N”,可以构建出如下二叉树的顺序存储形式:
```
L
D C
P F M
E H N
```
**链式存储**
同样通过字符串构建二叉树,但使用链式存储结构。
- **示例**:“LDPCFM###EH#N”,可以构建出如下二叉树的链式存储形式:
```
data: [L, D, C, P, F, M, E, H, N, L]
left: [2, 4, 0, 7, 0, 0, 0, 0, 0, 0]
right: [3, 5, 0, 8, 0, 0, 0, 0, 0, 0]
```
以上是关于树和二叉树的基础知识介绍,包括树的基本概念、二叉树的性质、存储结构以及如何构建二叉树等关键知识点。这对于理解算法设计中的树结构处理非常重要。