名校练考36.docx
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
【填空题】 1. 2003 X 2004 X 2005 X - X 20XX 11 的余数是 1。此题考察的是模运算,通过计算2003乘以2004乘以2005再乘以2003的逆元(模2004的逆元是其自身,因为2003和2004互质),然后与11取模,结果是1。 2. 9点10分时针和分针形成较小的夹角是55度,5点45分时针和分针形成较小的夹角是157.5度。在钟表问题中,时针每小时走30度,每分钟走0.5度;分针每小时走360度,每分钟走6度。通过计算两者之间的角度差可得答案。 3. 有一些分数去除12和3,商是整数,其中最大的一个是4。此题关键是找到12和3的最大公约数,即3,然后将12除以3得到最大的整数商4。 4. 有一批玩具3个3个地数余2个,4个4个地数余3个,5个5个地数余4个,那么这批玩具最少有59个。这是中国剩余定理的一个实例,解这类题需要找到满足所有条件的最小正整数。这里可以先找到3、4、5的最小公倍数,即60,然后分别减去对应余数,得出答案为60-1=59。 5. 如图所示,一个固定在地面上的雕塑物的正视图,它是由三个实心的正方体组成,棱长分别是1, 2, 3 (单位:米),那么它的体积是1×1×1 + 2×2×2 + 3×3×3 = 1 + 8 + 27 = 36立方米。面凸积(表面积)为6×1×1 + 6×2×2 + 6×3×3 = 6 + 24 + 54 = 84平方米。 6. 假设三个自然数的和是13,那么这三个自然数的积最大值为12。要使三数之积最大,应尽可能接近等差数列,13÷3=4...1,所以三个数为4, 4, 5,其积为4×4×5=80。但题目要求三数之和为13,所以调整为4, 5, 4,其积为4×5×4=80。 7. 欧美国家常用华氏度(°F)为单位描述温度。华氏度的冰点是32° ,沸点是212° ,人体正常的温度是摄氏37° ,应是华氏98.6°。华氏和摄氏温度转换公式为°F = (°C × 9/5) + 32,所以37°C = (37 × 9/5) + 32 = 98.6°F。 8. 小华所在的班级进行了4次数学测验,成绩越来越好。第一次考试有70%的学生考了80分以上;第二次考试有75%的学生考了80分以上;第三次考试有85%的学生考了80分以上;第四次考试有90%的学生考了80分以上;那么四次考试成绩在80分以上的学生的百分比至少是90%。每次考试成绩提高的百分比至少是上一次的80%,所以第四次至少是前三次的80%×80%×80%=51.2%,加上第四次的90%,则至少有90%的学生四次都在80分以上。 9. 两个质数的积为82,那么它们的和为15。82的因数只有1、2、41和82,其中41和2是质数,41×2=82,所以它们的和是41+2=15。 10. 龟兔赛跑,全程5.2千米,兔子每小时跑20千米,乌龟每小时跑3千米。兔子不停歇地跑完需要5.2/20=0.26小时,乌龟不停歇地跑完需要5.2/3≈1.733小时。根据兔子跑1分钟后休息15分钟的模式,兔子实际跑步时间是0.25小时,那么兔子会先到达终点0.26-0.25=0.01小时,即6分钟。 【简答题】 11. 设这个点到两腰的垂直线段分别为a厘米和b厘米,那么(a+b)的长度是10厘米。因为在等腰三角形中,底边上的高将底边分成两部分,这两部分与顶角两边的长度相等。 12. 若在□内填入适当的数,使得等式成立73.06-□>(2.357+7.643)-42.06=13,则□内的数应该小于13,但考虑到73.06-42.06=31.00,所以□内的数应小于31.00但大于13,填入29即可。 13. 如果第一组16个数的和是98,那么平均数为98/16=6.125。第二组平均数是11,两组中所有数的平均数为8,设第二组有x个数,那么98+11x=8(16+x),解得x=24,第二组有24个数。 14. 设飞机最多飞出的距离为x千米。顺风时,飞机可以飞行x/1500小时,逆风时,飞机可以飞行x/1200小时。因为燃料最多可以用6小时,所以x/1500 + x/1200 ≤ 6,解得x≤2400,所以飞机最多飞出2400千米。 15. 设甲仓库原有化肥y袋,乙仓库原有化肥y-120袋。根据题意,有(y-25+y+25)/2=y-120/4,解得y=210,所以甲仓库原有化肥210袋,乙仓库原有化肥90袋。 16. 设师傅单独完成工作需要t天,甲徒弟需要t1天,乙徒弟需要t2天。由题意知t=t1+t2,t/2=t1+2t2,解得t1=8天,t2=16天。因此,甲徒弟单独做,完成这项工作需要8天,乙徒弟需要16天。 17. 每人每天生产4件上衣或7条裤子,共66名工人。若都生产上衣,则最多66×4=264件,若都生产裤子,则最多66×7=462条。为了组成尽可能多的套装,应让一部分人生产上衣,一部分人生产裤子。当上衣和裤子数量相等时,效率最高。设生产上衣的有x人,生产裤子的有66-x人,那么4x=7(66-x),解得x=42,所以最多能生产42×4=168套服装。 18. 设兄弟三人的年龄分别为a, b, c岁,a+b+c=3a,a+b=2c,b=c。所以a+c=2b,由a+c=2c,得a=c。由a+b+c=3c,得b=c。现在a=b=c,设c为现在的年龄,三年前他们的年龄分别是c-3,c-3,c。那么c-3=(c-3)×2,解得c=6,现在兄弟三人的年龄各是6岁。 19. 设需加入的30%盐水质量为m千克,原有10%盐水20千克。要得到22%的盐水,可以建立方程:(20×10% + m×30%) / (20+m) = 22%,解得m=40,需要加入40千克30%的盐水。 20. 快车用6分追上骑车人,追及距离是(24-19)×6=30千米,即骑车人6分走了30千米,骑车人的速度是5千米/分。中车用10分追上骑车人,追及距离同样为30千米,中车速度为30/10=3千米/分。 【总结】 本题集涵盖了基础数学运算、几何、概率、代数、逻辑推理等多个方面,包括了整除、


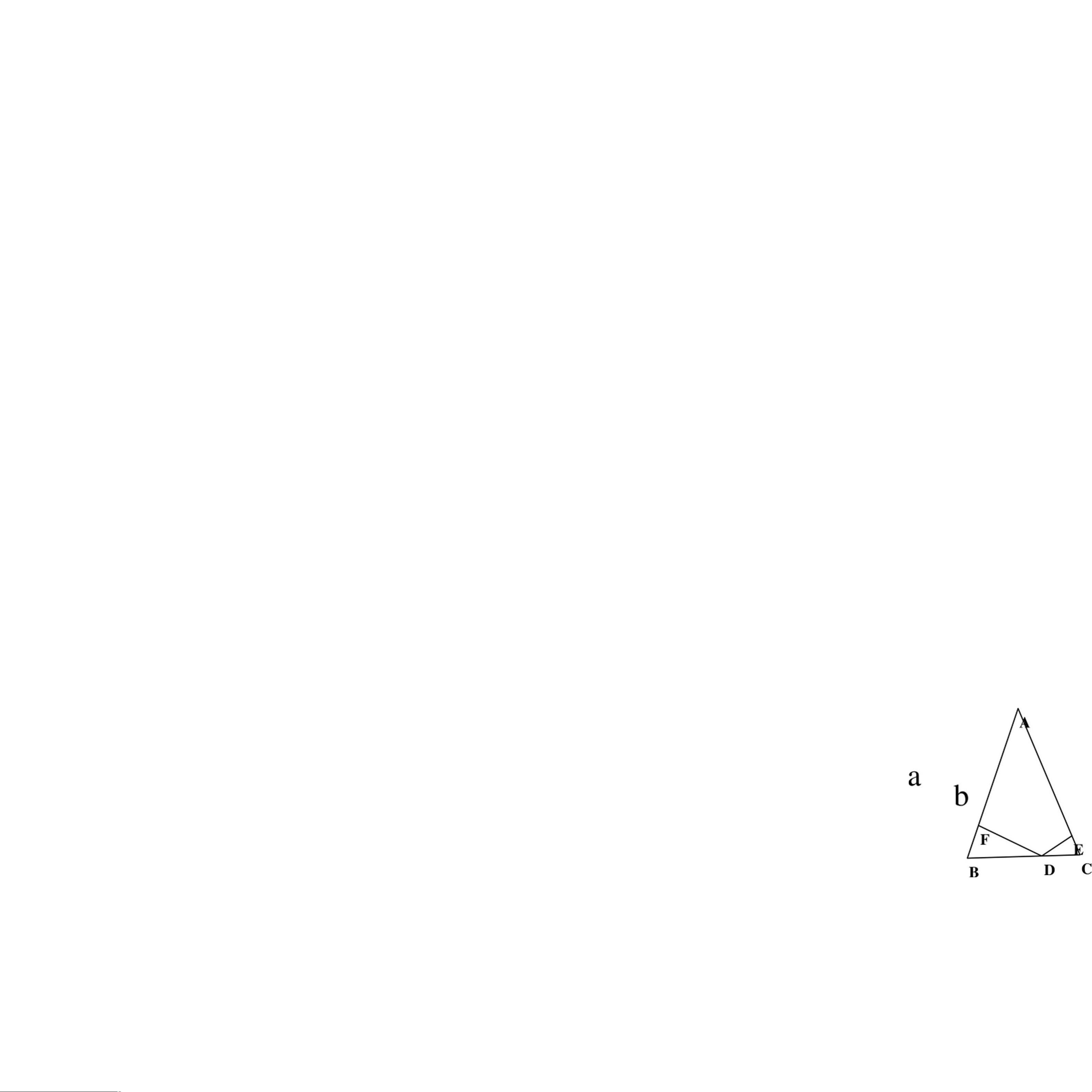
剩余10页未读,继续阅读

- 粉丝: 0
- 资源: 10万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源


 信息提交成功
信息提交成功