数据结构考研

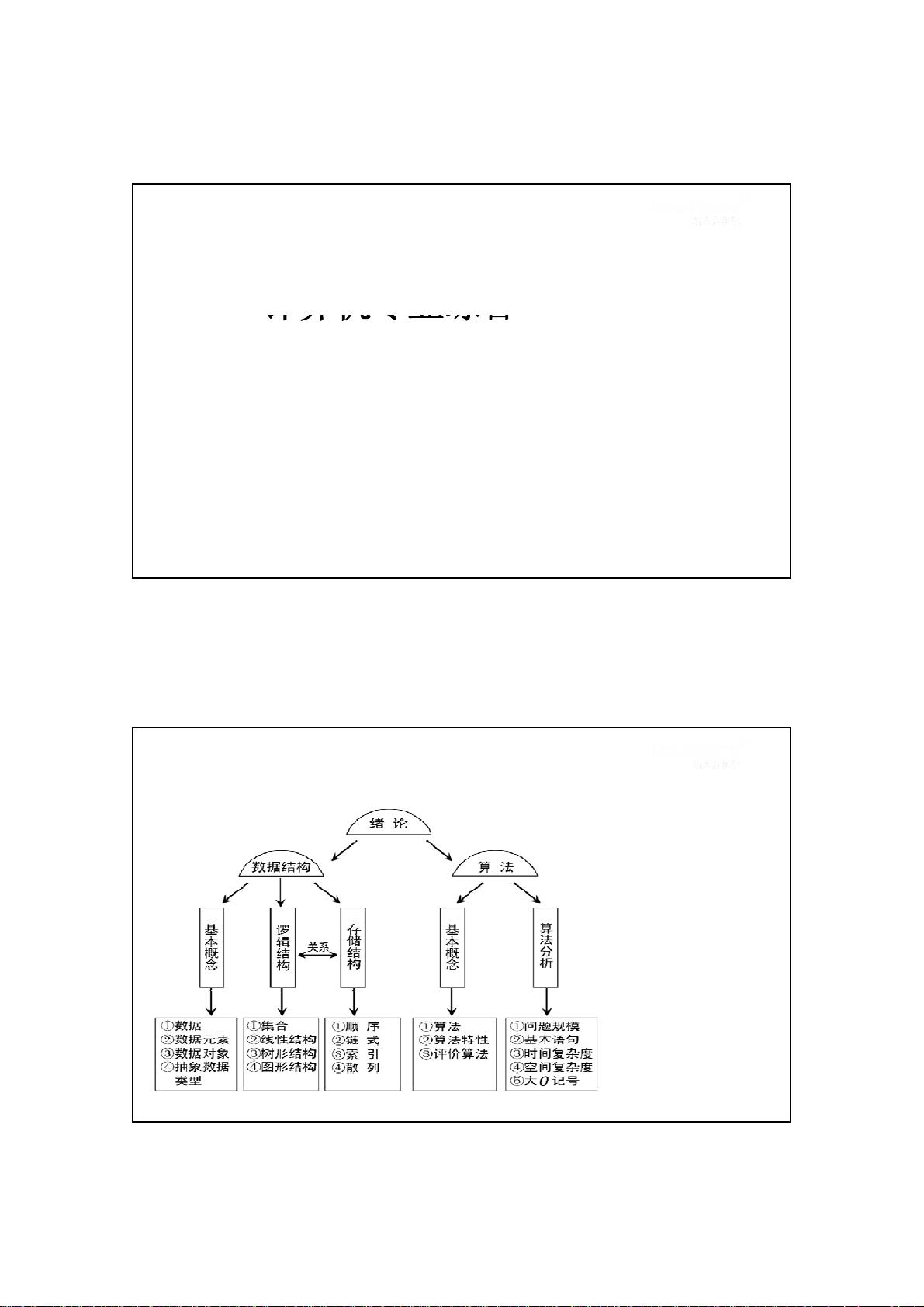
数据结构是计算机科学中的核心课程，对于考研的学生来说尤其重要。新东方的考研书讲义提供了关于数据结构的深入理解，特别是关注算法的设计和效率评估。 算法设计的正确性是首要标准，确保算法能正确解决问题。可读性至关重要，便于其他开发者理解和维护。健壮性是指算法对异常输入的处理能力，应能稳定运行不受错误数据的影响。效率和存储量需求是评价算法性能的关键指标，效率通常用算法执行时间来衡量，而存储量需求则关乎内存占用。 算法效率的衡量有两种主要方法：事后统计法和事前分析估算法。事后统计法是在实际运行后统计运行时间，而事前分析估算法则是在算法设计阶段通过分析其基本操作的执行次数来预估效率。在分析算法时间复杂度时，我们通常使用大O符号（O notation）来描述算法的渐近时间复杂度。例如，如果算法执行时间随问题规模n的增长率与f(n)相同，那么可以表示为T(n) = O(f(n))。 算法的时间复杂度可以通过分析算法中的基本操作及其执行次数来估算。基本操作是指在特定问题中频繁执行的操作，算法的运行时间与其执行次数成正比。同时，除了算法本身，影响执行时间的因素还包括问题规模、编程语言、编译器质量和计算机硬件性能。 在讨论算法的空间复杂度时，关注的是算法运行过程中所需存储空间的增长率，可以用S(n) = O(g(n))来表示。空间复杂度分析包括输入数据、程序本身和辅助变量所占空间。原地工作算法是指其额外存储空间相对于输入数据量来说是常数。如果存储需求依赖于特定输入，则需考虑最坏情况。 线性表是一种基础数据结构，包含相同数据类型的n个元素，可以是顺序表或链表等形式。顺序表通常分为静态分配和动态分配两种，静态分配在固定大小的数组中存储元素，而动态分配则根据需要动态扩展数组。顺序表的一个显著特点是支持按序号随机访问，时间复杂度为O(1)。按值查找的时间复杂度取决于查找元素的位置和表的长度，平均比较次数会受到这些因素的影响。 数据结构考研涵盖的内容广泛，包括但不限于算法设计原则、效率分析、空间复杂度评估以及具体数据结构如线性表的操作和实现。对于准备考研的学生来说，理解和掌握这些概念是至关重要的，因为它们是计算机科学领域的基石，直接影响到程序设计的性能和效率。