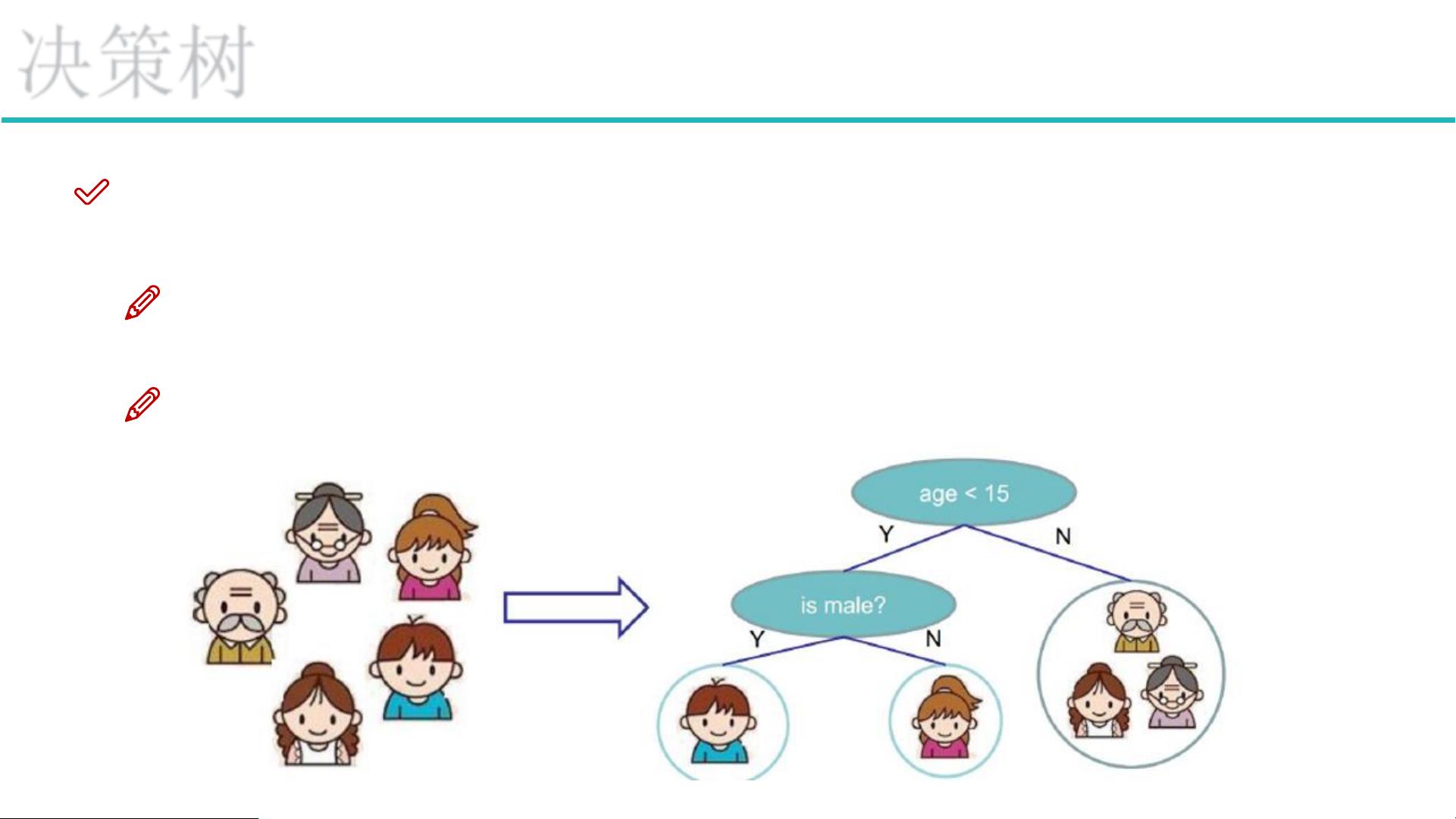
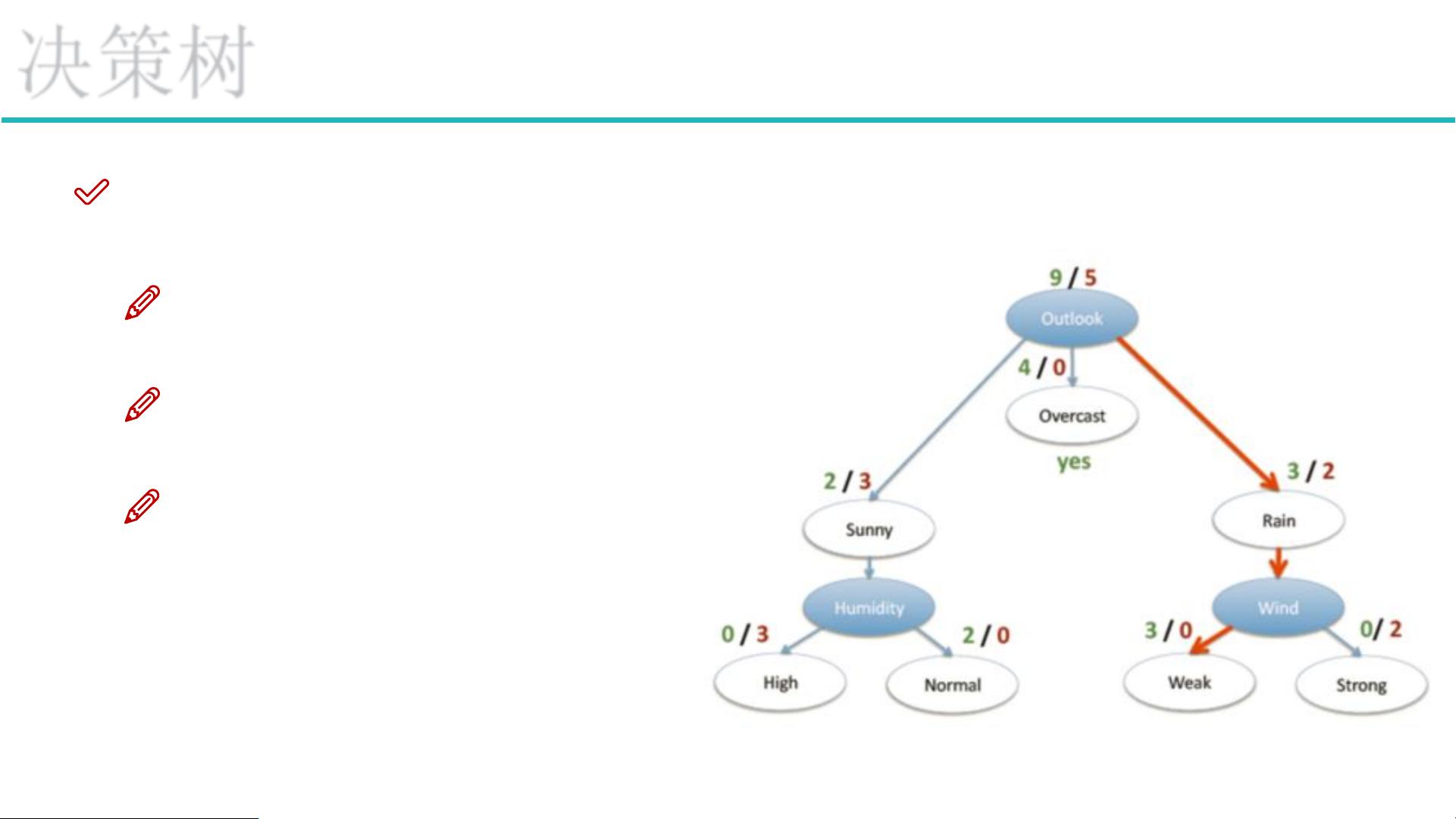
决策树与集成算法

### 决策树与集成算法 #### 决策树概述 **决策树**是一种监督学习方法，用于分类和回归任务。它通过构建一棵树形结构，从根节点开始，逐步根据特征的不同取值做出判断，直到达到叶子节点，从而得出最终的决策结果。 #### 树的组成部分 1. **根节点**：树的第一个节点，通常用来表示数据集中的所有实例，从这里开始进行特征的选择和划分。 2. **非叶子节点与分支**：这些节点代表了对数据的进一步划分，每个非叶子节点都会根据某个特征的不同取值指向不同的分支。 3. **叶子节点**：决策树的终端节点，不再进一步划分，直接给出分类或回归的结果。 #### 决策树的训练与测试 - **训练阶段**：基于训练数据集构建决策树。关键在于如何选择最佳特征进行分割，常见的方法包括使用信息增益、信息增益比或GINI指数等作为评估标准。 - **测试阶段**：利用构建好的决策树对新的数据进行分类或回归预测。对于每条新数据，沿着决策路径从根节点到某个叶子节点，最终到达的叶子节点即为预测结果。 #### 特征选择与切分 - **信息增益**：衡量特征在分类中提供的信息量，用于指导特征的选择。选择具有最高信息增益的特征作为分割特征。 - **熵**：衡量数据集中样本的不确定性，熵越高表明样本的不确定性越大。通过计算分裂前后的熵变化，可以确定特征的最佳分割点。 - **信息增益率**：修正了信息增益偏向于选择具有较多取值的特征的问题。 - **GINI指数**：另一种衡量特征分割效果的方法，适用于二分类或多分类问题，计算简便且不易过拟合。 #### 决策树构造实例 以天气因素（如晴天、阴天、雨天）是否适合打高尔夫球为例： - 假设有14天的数据记录，其中9天适合打球，5天不适合。 - 通过计算各特征（例如天气状况、温度、湿度、风力）的信息增益，选择信息增益最大的特征作为根节点。 - 重复上述过程，直至达到停止条件（如达到最大深度、最小样本数量等）。 #### 决策树算法 - **ID3**：基于信息增益的决策树算法，但容易受到具有较多取值的特征的影响。 - **C4.5**：改进版的ID3算法，使用信息增益比来选择特征，更好地处理具有不同取值数量的特征。 - **CART**：用于回归和分类任务，使用GINI系数作为分割标准。 #### 决策树剪枝策略 - **预剪枝**：在树生长过程中进行剪枝，避免过拟合，如限制树的最大深度、叶子节点的最小样本数等。 - **后剪枝**：先生成完整的决策树，再通过交叉验证等方式去除那些降低泛化能力的子树。 #### 集成算法 - **Bagging**：通过自助采样法创建多个数据集，对每个数据集训练一个模型，最后通过投票或平均来决定最终结果。典型应用是**随机森林**，它通过数据和特征的随机性增强了模型的多样性和鲁棒性。 - **Stacking**：将多种模型的输出组合起来形成更强大的模型，通常分为两阶段：第一阶段训练基础模型，第二阶段使用基础模型的输出训练元模型。 - **Boosting**：一系列弱学习器通过迭代的方式被增强为强学习器，每次迭代中，新加入的学习器都试图纠正之前学习器的错误。**AdaBoost**是最著名的Boosting算法之一。 决策树是一种直观且易于理解的机器学习模型，但在实际应用中可能会遇到过拟合等问题。集成算法则通过结合多个模型的优势，提高了预测性能和稳定性。