数值分析实验题(-华科).doc
2.虚拟产品一经售出概不退款(资源遇到问题,请及时私信上传者)
【数值分析实验题——多项式插值的振荡现象】 在数值分析中,多项式插值是一种常见的近似方法,用于构建一个多项式函数来精确地通过一组给定的离散数据点。这个实验主要探讨了在固定区间上,随着插值节点数量的增加,拉格朗日插值多项式的性质,特别是它对于函数逼近的效果,以及可能出现的振荡现象,即Runge现象。 Runge现象是由德国数学家Carl Runge于19世纪末发现的,它揭示了一个有趣的现象:当我们在一个较大区间内使用等间隔的节点进行高次多项式插值时,插值多项式可能在节点间产生剧烈的振荡,导致插值结果远离原函数。这个现象对于数值计算来说是个挑战,因为它意味着高次插值并不总能提供更好的近似。 实验内容涉及两个部分: 1. 在区间[-1,1]上,使用等距离划分的节点,构建拉格朗日插值多项式`Ln(x)`。当节点数n逐渐增加(n=2,3,...)时,绘制原函数`f(x)`及`Ln(x)`的图形,并对比分析。观察随着节点数增加,插值多项式的行为是否更接近原函数,还是出现了振荡现象。 2. 对其他函数,如定义在[-5,5]上的函数`h(x)`,重复上述实验,观察Runge现象是否普遍存在于各种函数中。 实验结果表明,对于函数`f(x)`,随着插值点的增加,拉格朗日插值多项式`Ln(x)`的振荡现象逐渐明显。当n=2时,插值效果尚可,但随着n的增加,`Ln(x)`的波动变得越来越大,甚至在某些区域偏离原函数`f(x)`。同样,对于函数`h(x)`,随着n的增大,振荡现象也逐步出现,尤其是在n=7时,波动尤其剧烈。 这种振荡现象的出现主要是由于等间隔节点的选择。等间隔节点容易导致高次插值多项式对高频率成分过度放大,从而引起插值结果的不稳定性。为了避免Runge现象,可以采用更合理的节点分布,比如Chebyshev节点,它们在区间两端更密集,能更好地抑制高次项的影响。 总结来说,这个实验强调了在数值插值中选择合适节点的重要性,以及理解并避免Runge现象对于提高插值精度的关键性。对于实际应用,我们应当谨慎选择插值方法和节点分布,以确保得到的近似结果既稳定又准确。此外,对Runge现象的研究也促进了插值理论的发展,比如产生了多项式插值的替代方法,如最小二乘插值和样条插值,这些方法在处理类似问题时表现出更好的性能。

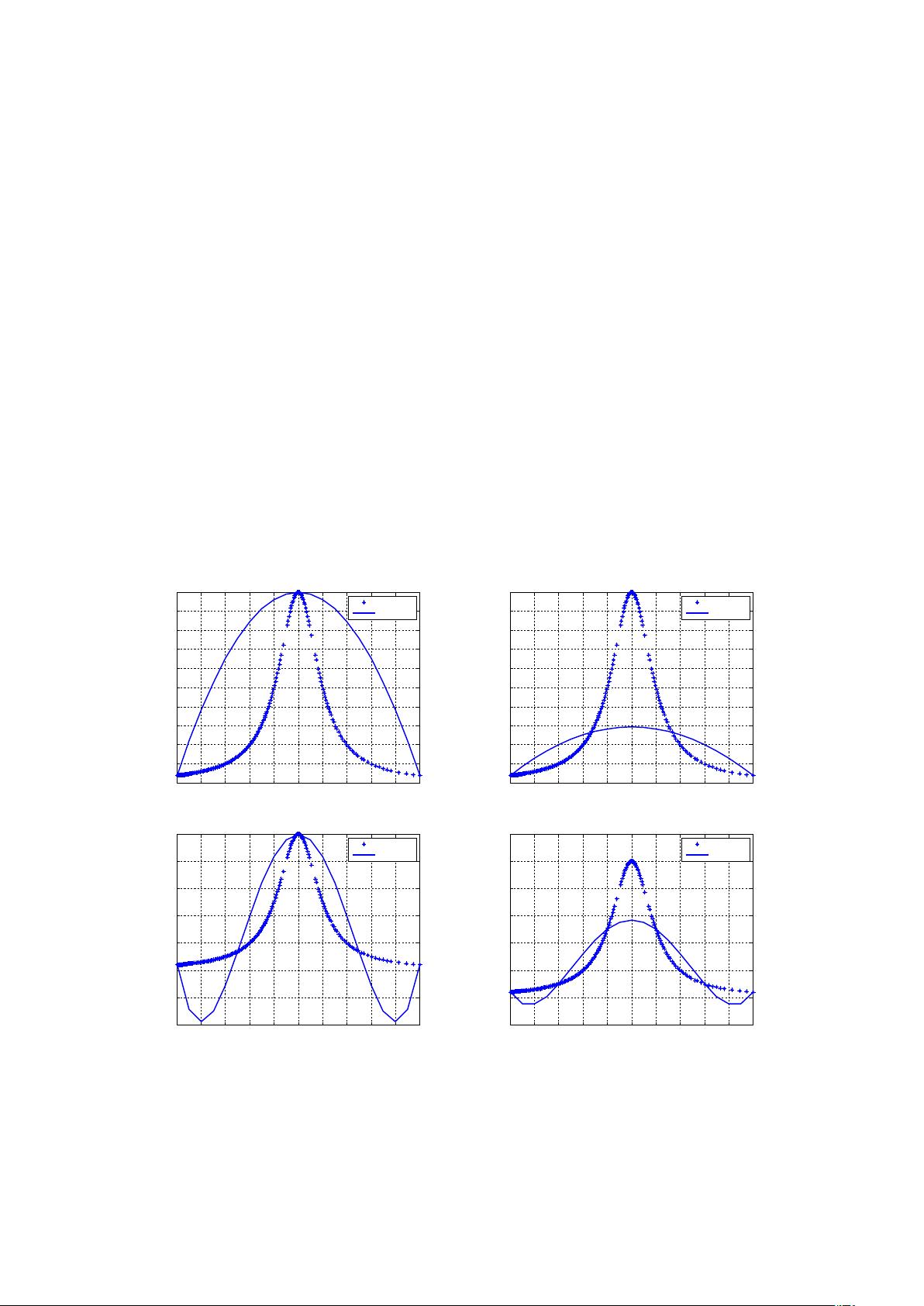
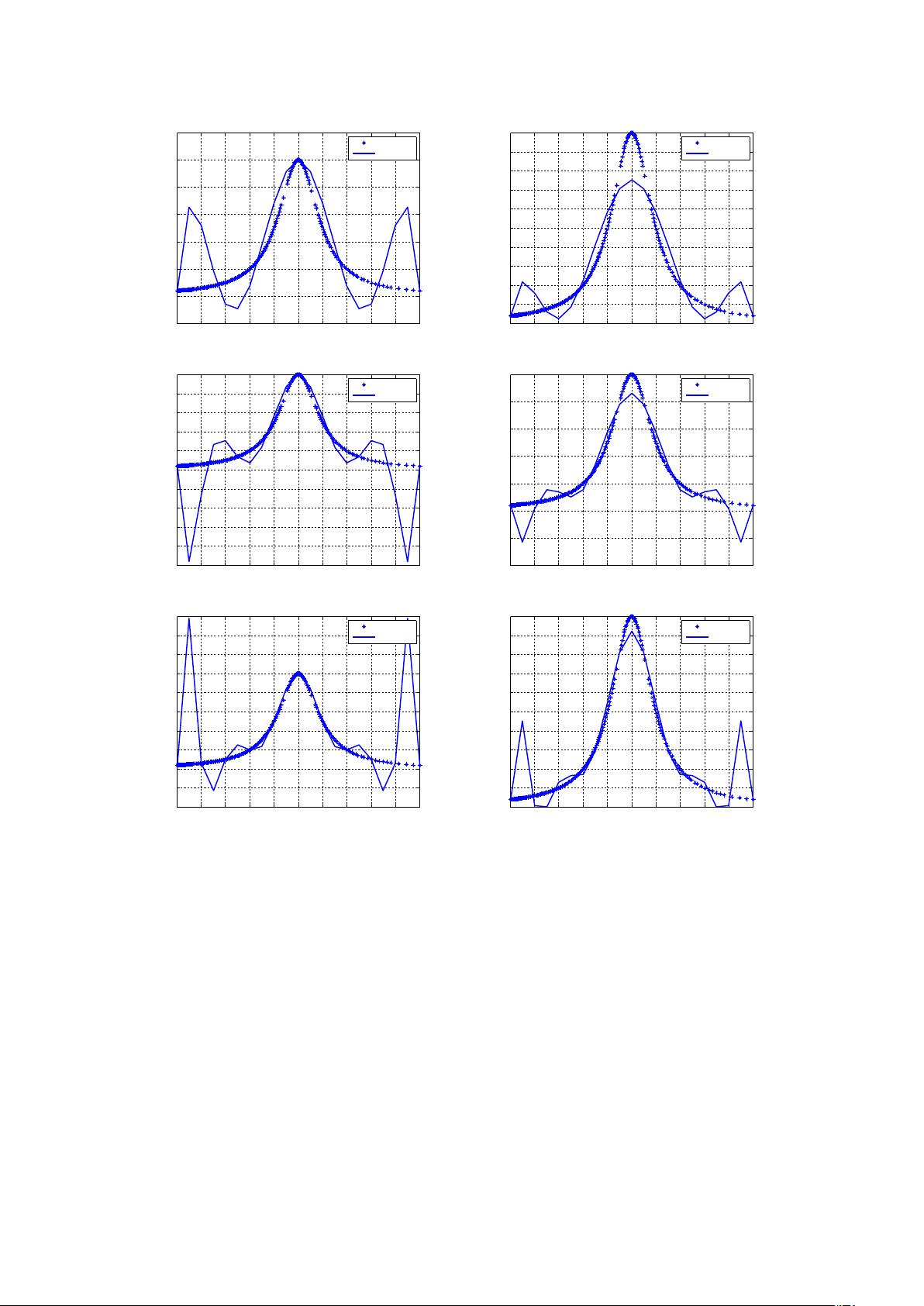
剩余12页未读,继续阅读

- 粉丝: 0
- 资源: 4万+
 我的内容管理
展开
我的内容管理
展开
 我的资源
快来上传第一个资源
我的资源
快来上传第一个资源
 我的收益 登录查看自己的收益
我的收益 登录查看自己的收益 我的积分
登录查看自己的积分
我的积分
登录查看自己的积分
 我的C币
登录后查看C币余额
我的C币
登录后查看C币余额
 我的收藏
我的收藏  我的下载
我的下载  下载帮助
下载帮助

 前往需求广场,查看用户热搜
前往需求广场,查看用户热搜最新资源
- IP网络的仿真及实验.doc
- 学习路之uniapp-goEasy入门
- 多边形框架物体检测26-YOLO(v5至v11)、COCO数据集合集.rar
- 基于Python和OpenCV的人脸识别签到系统的开发与应用
- course_s2_ALINX_ZYNQ_MPSoC开发平台Vitis应用教程V1.01.pdf
- 基于51单片机开发板设计的六位密码锁
- course_s5_linux应用程序开发篇.pdf
- course_s4_ALINX_ZYNQ_MPSoC开发平台Linux驱动教程V1.04.pdf
- course_s0_Xilinx开发环境安装教程.pdf
- 多边形框架物体检测20-YOLO(v5至v11)、COCO、CreateML、Paligemma、TFRecord、VOC数据集合集.rar


 信息提交成功
信息提交成功