Hough 变换
Hough 变换是图像处理中从图像中识别几何形状的基本方法之一,适用于规
则的人造物体图像,Hough 变换的基本原理在于利用点与线的对偶性,将原始图
像空间的给定的曲线通过曲线表达形式变为参数空间的一个点。这样就把原始图
像中给定曲线的检测问题转化为寻找参数空间中的峰值问题。也即把检测整体特
性转化为检测局部特性。比如直线、椭圆、圆、弧线等。
霍夫变换于 1962 年由 Paul Hough 首次提出[53],后于 1972 年由 Richard
Duda 和 Peter Hart 推广使用[54],经典霍夫变换用来检测图像中的直线,后来霍
夫变换扩展到任意形状物体的识别,多为圆和椭圆。
为了把边缘点连成曲线函数,需要:
1.把经过每个边缘点的所有可能的曲线函数(一个函数族)的函数在参数空
间中计数
2.找出计数最大的参数
3.在边缘图像中画出该参数对应的曲线
1.1 直线检测
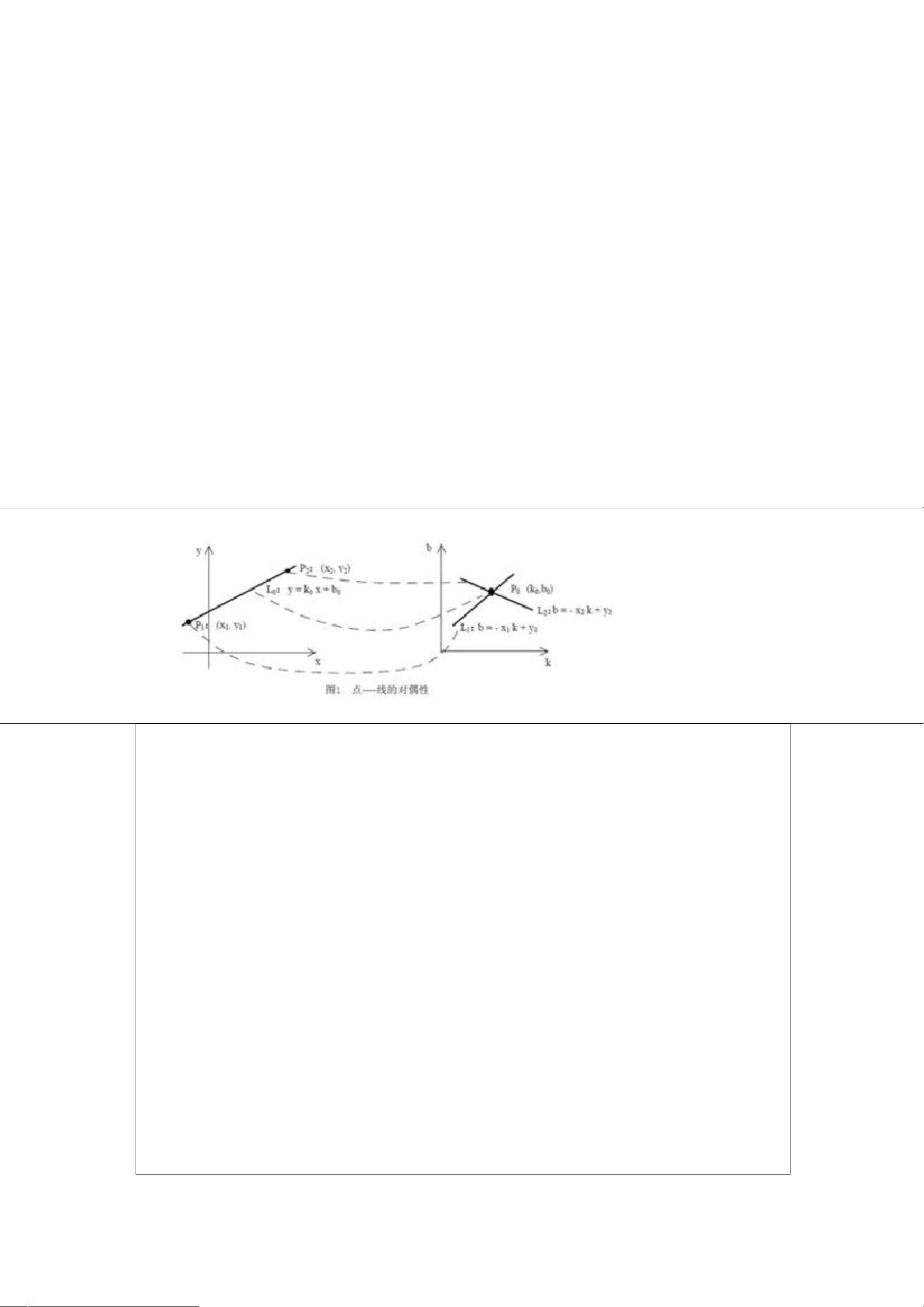
设已知一黑白图像上画了一条直线,要求出这条直线所在的位置。我们知道,
直线的方程可以用 y=k*x+b 来表示,其中 k 和 b 是参数,分别是斜率和截距。
过某一点(x0,y0)的所有直线的参数都会满足方程 y0=kx0+b。即点(x0,y0)确定了
一族直线。方程 y0=kx0+b 在参数 k--b 平面上是一条直线,(你也可以是方程
b=-x0*k+y0 对应的直线)。这样,图像 x--y 平面上的一个前景像素点就对应到参
数平面上的一条直线。我们举个例子说明解决前面那个问题的原理。
设图像上的直线是 y=x, 我们先取上面的三个点:A(0,0), B(1,1), C(22)。可
以求出,过 A 点的直线的参数要满足方程 b=0, 过 B 点的直线的参数要满足方程
1=k+b, 过 C 点的直线的参数要满足方程 2=2k+b, 这三个方程就对应着参数平面
上的三条直线,而这三条直线会相交于一点(k=1,b=0)。
同理,原图像上直线 y=x 上的其它点(如(3,3),(4,4)等) 对应参数平面上的直
线也会通过点(k=1,b=0)。这个性质就为我们解决问题提供了方法,就是把图像平















