算法分析若干实例问题解析.pdf

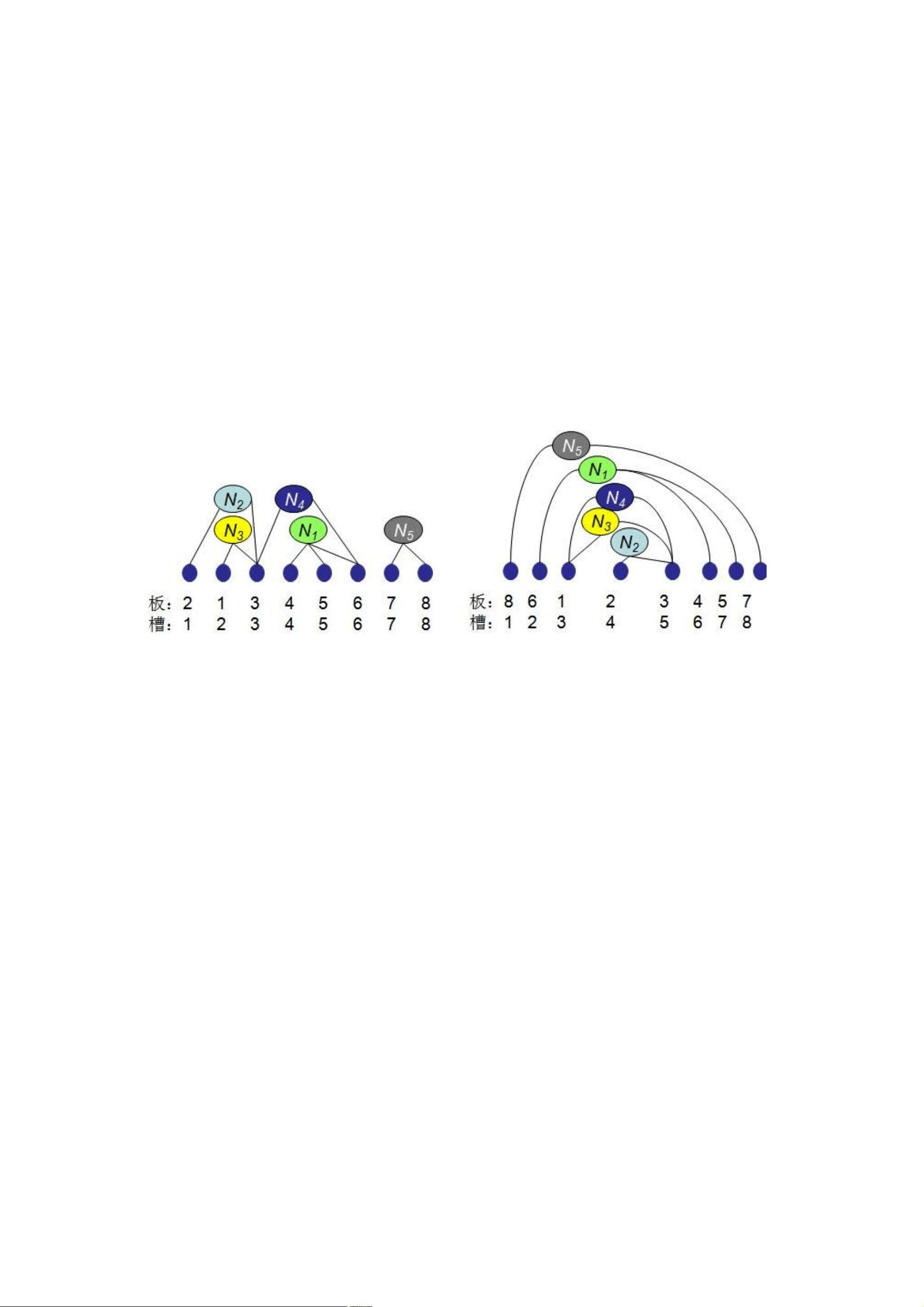
《算法分析若干实例问题解析——最小长度电路板排列问题》 最小长度电路板排列问题，源于大规模电子系统设计，旨在优化电路板的排列方式，以减小连接块的最大长度。问题的基本设定是，有n块电路板需要插入含有n个插槽的机箱中，电路板之间由m个连接块相互连接。每个连接块包含B集合中的一部分电路板，且这些电路板通过同一根导线相连。连接块的长度定义为从第一个电路板到最后一个电路板的插槽距离。目标是寻找一种排列方式，使m个连接块中的最大长度最小化。 例如，给定n=8，m=5的情况，我们可以有8块电路板及5个连接块的组合。通过分析电路板的排列，可以计算出各个连接块的长度，并据此评估排列的优劣。在解决此类问题时，我们需要注意的是，由于其NP难的特性，无法直接找到一个简单的多项式时间算法来解决。常见的算法如分治、贪婪和动态规划在此问题上并不适用。 在解决策略上，回溯法和分支限界法成为了有效的工具。回溯法是一种系统地搜索问题解空间的算法，它通过构造部分解决方案并逐步扩展，直到找到完整解或者发现无法继续扩展为止。在电路板排列问题中，我们可以构建一个排列树，通过不断交换电路板的位置来尝试不同的排列，同时检查是否满足约束条件（即连接块的正确连接）和边界条件（最大长度是否优于当前最优解）。 分支限界法则是另一种搜索策略，它避免了回溯法中可能的无效搜索，通过剪枝操作减少搜索空间。在这个问题中，我们可以维护当前最大长度（nowl）和最优最大长度（minl），每次尝试新的排列时，如果新产生的最大长度大于或等于minl，则立即剪枝，不再继续搜索该分支，以此提高效率。 具体实现时，可以创建一个名为`minBoard`的类，包含最小最大长度（minl）、当前最大长度（nowl）以及存储各种状态的数组，如`low`和`high`数组记录连接块的左右边界，`x`和`bestx`数组分别表示当前解和最优解。通过递归函数`backtrack`进行回溯搜索，每次递归增加电路板的排列，同时更新最大长度，只有当新的最大长度小于最优最大长度时，才继续探索子树。 最小长度电路板排列问题是一个典型的组合优化问题，适合采用回溯法或分支限界法求解。在实际应用中，这种问题的求解不仅需要深入理解算法原理，还需要灵活运用数据结构和优化技巧，以提高算法的效率和准确性。