自己写的浮点数计算误差分析

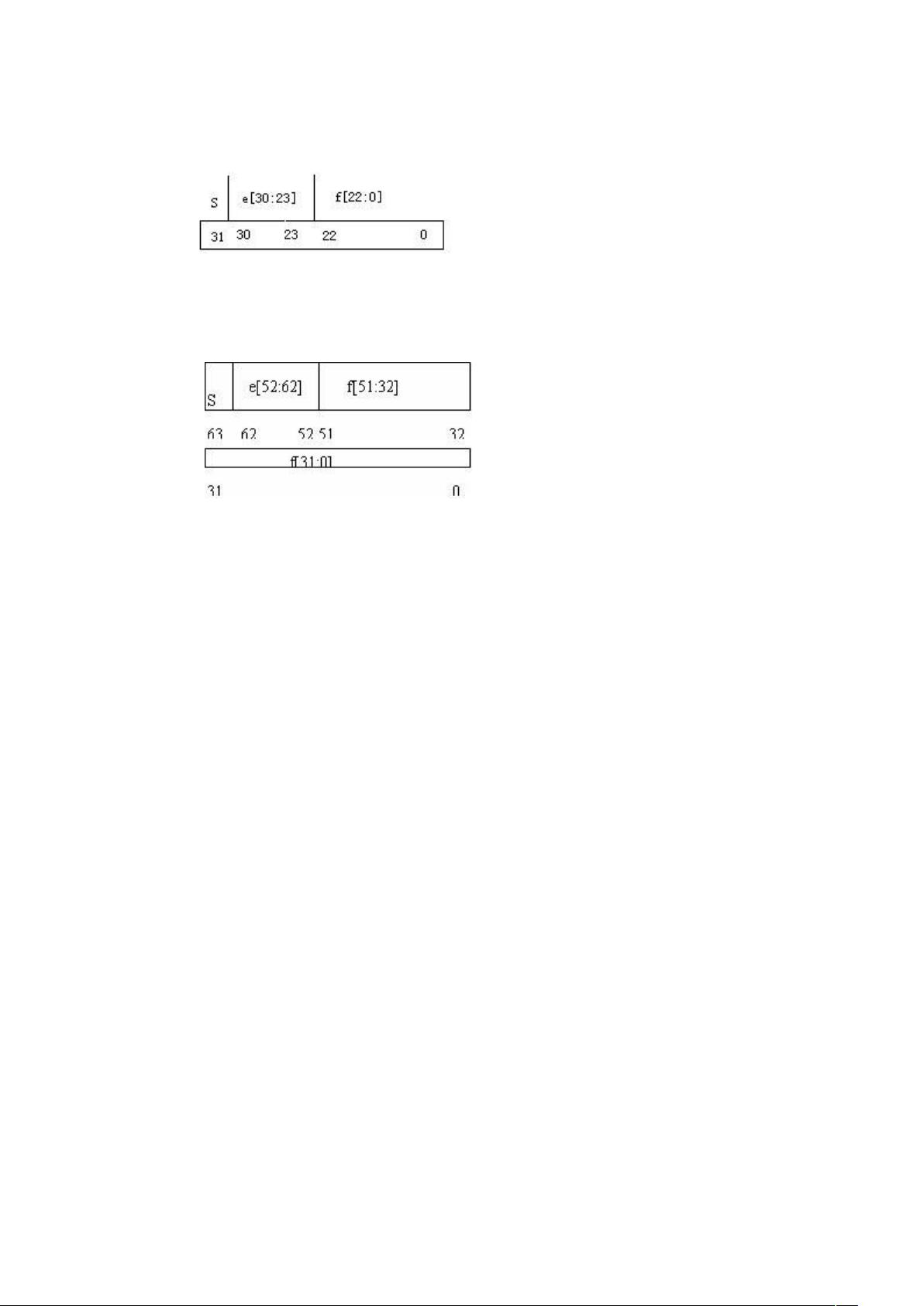
浮点数计算是计算机科学中的一个关键领域，特别是在数值计算、科学计算以及工程应用中扮演着重要角色。然而，由于浮点数在计算机中的表示方式和计算过程中的限制，浮点计算往往会产生误差。这篇自己编写的分析文章深入探讨了浮点计算误差的来源，并提出了一些实用的避免误差的方法。 我们要理解浮点数在计算机中的表示。计算机使用二进制来存储和处理数据，而浮点数在十进制中是无限不循环的小数。在二进制下，大多数十进制小数不能精确表示，这导致了浮点数的第一个误差来源——舍入误差。例如，0.1在二进制下是无限不循环的，因此计算机必须进行近似，这就产生了误差。 浮点计算遵循IEEE 754标准，该标准定义了浮点数的存储格式和运算规则。浮点数分为不同的精度级别，如单精度（32位）和双精度（64位）。精度的不同意味着存储的位数有限，导致更大的数可能无法完全表示，产生精度损失。 再者，浮点运算过程中也会产生误差。加法、减法、乘法和除法等基本运算在二进制浮点数表示下不是封闭的，即结果可能无法精确表示为原浮点数类型。此外，算术运算的顺序也会影响结果的精确度，因为计算机会先进行内部转换再进行运算，这一过程可能导致额外的误差积累。 为了避免或减少浮点计算的误差，有几种策略可以采用。一种是使用更高的精度，如从单精度切换到双精度，尽管这会增加计算时间和内存需求。另一种是使用特定的算法或库，比如高精度库，它们提供更精确的计算，但同样会牺牲效率。还有一种是利用数值稳定性的概念，选择对误差不敏感的算法，或者在必要时进行误差控制和校正。 在实际编程中，可以使用特定的函数，如`fma`（乘加）函数，它可以合并乘法和加法操作，减少中间结果的舍入误差。此外，理解和使用舍入模式，如`round-to-nearest`和`round-towards-zero`，可以帮助控制误差的方向。 进行误差分析和测试也是必不可少的步骤。通过比较精确解和浮点计算结果，可以评估误差的大小和分布，找出可能的问题源。对于关键的计算任务，可以引入容错机制，如设置误差边界或使用容差检查，确保结果的合理范围。 浮点数计算误差是一个复杂而重要的主题，需要我们理解其来源并采取适当的策略来控制。通过深入学习和实践，我们可以更好地理解和应对这些误差，提高计算的准确性和可靠性。