数字图像变换与变换编程

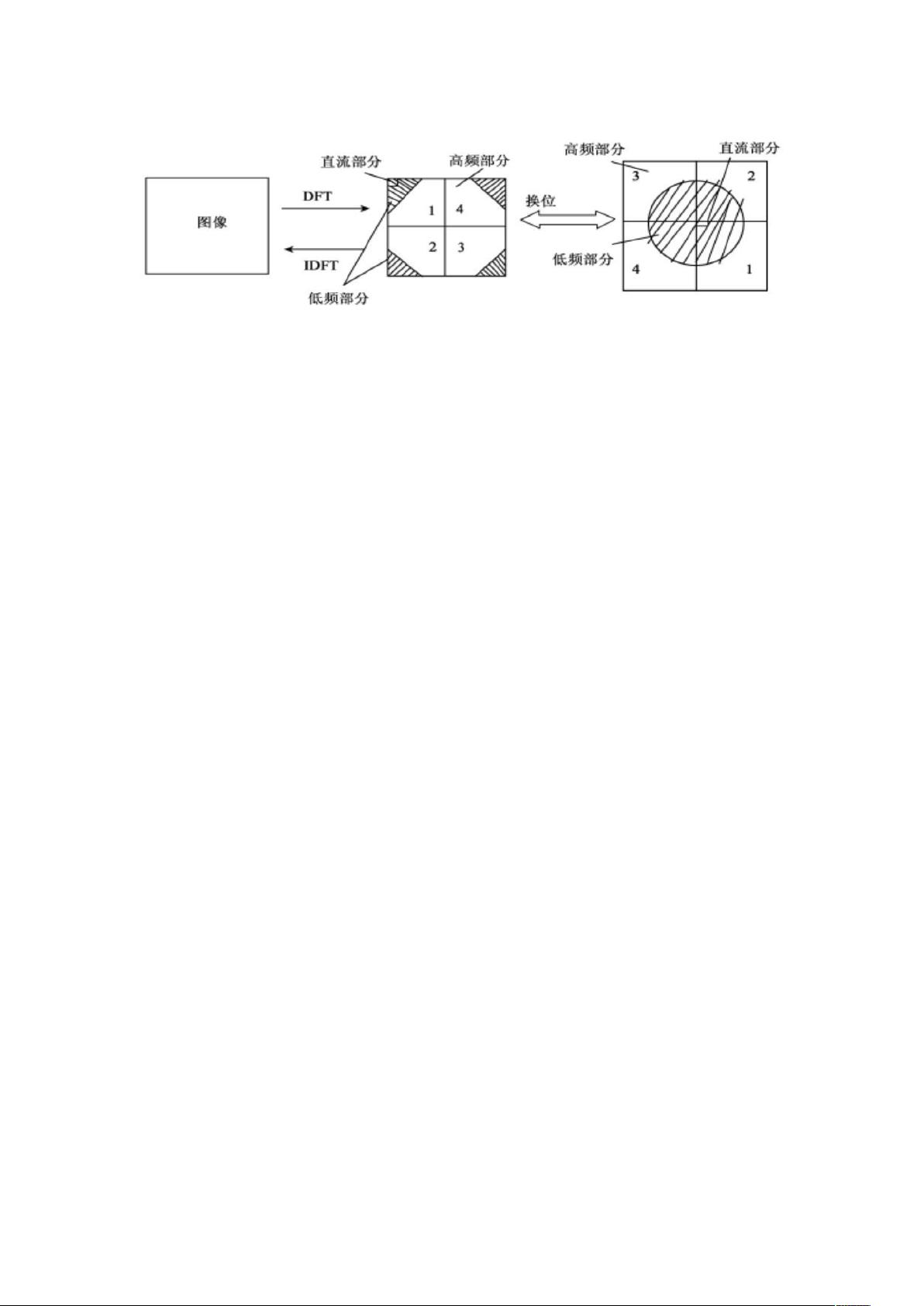
在计算机图像处理中，图像信号变换是一种为了达到某种目的( 通常是从图像中获取某种重要信息) 而对图像使用的一种数学技巧， 经过变换后的图像将更为方便和容易地处理和操作。图像变换在图像处理中有着非常重要的地位， 在图像增强、图像分析、图像复原、图像编码压缩以及特征抽取方面有着广泛的应用。特别是在信息隐藏方面有着非常重要的作用。 在计算机图像处理领域，图像变换是一项关键的技术，它利用数学工具改变图像的表示方式，以适应不同的处理需求。图像变换的主要目标是从图像中提取重要信息，便于后续的图像增强、分析、复原、编码压缩以及特征抽取。尤其在信息隐藏领域，图像变换扮演着至关重要的角色。 数字图像变换通常是通过应用特定的数学函数，如傅里叶变换，来完成的。傅里叶变换是一种揭示函数频率成分的工具，它可以将图像从空间域转换到频率域。在频率域中，图像的能量分布情况得以清晰展示，高频部分代表图像的细节，而低频部分则包含图像的主要结构信息。 离散傅里叶变换（DFT）是傅里叶变换在计算机中的实际应用形式，它适用于离散信号的处理。对于MxN大小的图像，DFT将图像的每个像素点与一组复数正弦波相乘并求和，生成频域表示F(p,q)。F(p,q)的每个元素表示对应频率成分的幅度和相位，其中p和q分别对应X轴和Y轴的频率。DFT的周期性使得通常只需要关注-π到π的频率范围。DC分量F(0,0)代表图像的整体亮度或平均值。 在实际计算中，DFT的复杂度较高，需要O(N^2)的运算量。然而，快速傅里叶变换（FFT）算法提供了一种更高效的解决方案，将计算复杂度降低到O(Nlog2N)。当N为2的幂时，FFT的效率最高。快速卷积是利用FFT实现的，通过先对两个图像进行傅里叶变换，然后在频域中进行乘法操作，最后逆傅里叶变换回空间域，实现图像的卷积。 以给定的代码为例，展示了如何使用FFT进行快速卷积。首先创建两个矩阵A和B，然后对它们进行二维傅里叶变换，得到A2和B2。接着，将这两个变换结果相乘，得到乘积M，再对M进行逆傅里叶变换，最终得到卷积结果C。 数字图像变换是图像处理的核心技术之一，它通过数学变换揭示图像的内在特性，为各种图像处理任务提供了基础。傅里叶变换及其快速算法在图像分析、压缩和信息隐藏等方面有着广泛的应用，并且通过快速卷积，使得复杂的卷积运算变得高效且易于理解。