
几种特殊图的介绍

1. 二部图 ( 偶图 )
引例 : 有 4 个工人 a
1
,a
2
,a
3
,a
4
,4 项任务 b
1
,b
2
,b
3
,b
4
, 已知 a
1
熟悉任务 b
1
,b
2
,b
3
,
a
2
熟悉 b
2
,b
3
, a
3
只熟悉 b
4,
a
4
熟悉 b
3
,b
4
. 问怎么分配工人 , 才能使每
人都有任务 , 每项任务都有人来完成 ?
做顶点集 V={a
1
,a
2
,a
3
,a
4
,b
1
,b
2
,b
3
,b
4
},
若 a
i
熟悉任务 b
j
, 则在 a
i
与 b
j
之间连
边 ,
则得无向图 G
b
1
b
2
b
3
b
4
a
1
a
2
a
3
a
4
1.1 二部图定义 :
若能将无向图 G=<V,E> 的顶点集 V 分成两个子集 V
1
和 V
2
(V
1
∩V
2
= ), 使得 G 中任一边的两个端点都一个属于 V
1
,
另一个属于 V
2
, 则称 G 为二部图 . 此时 ,G 记为 <V
1
,V
2
,E >.

1.2 完全二部图 :
二部图 G=< V
1
,V
2
,E >, 若 V
1
中任一顶点与 V
2
中每一顶点
都有且仅有一条边关联 , 则称 G 为完全二部图 . 若此时有
, 则记完全二部图 G 为 K
r,s
sVrV
21
,
完全二部图 K
r,s
的顶点数 n=r+s ,边数 m=rs.
1.3 二部图的判断 : 练习 P
177/188
无向图 G=< V,E > 为二部图 G 中无奇数长度的回路。
图标法 : 从一点开始画黑点 , 相邻点为白点 , 依次标 .
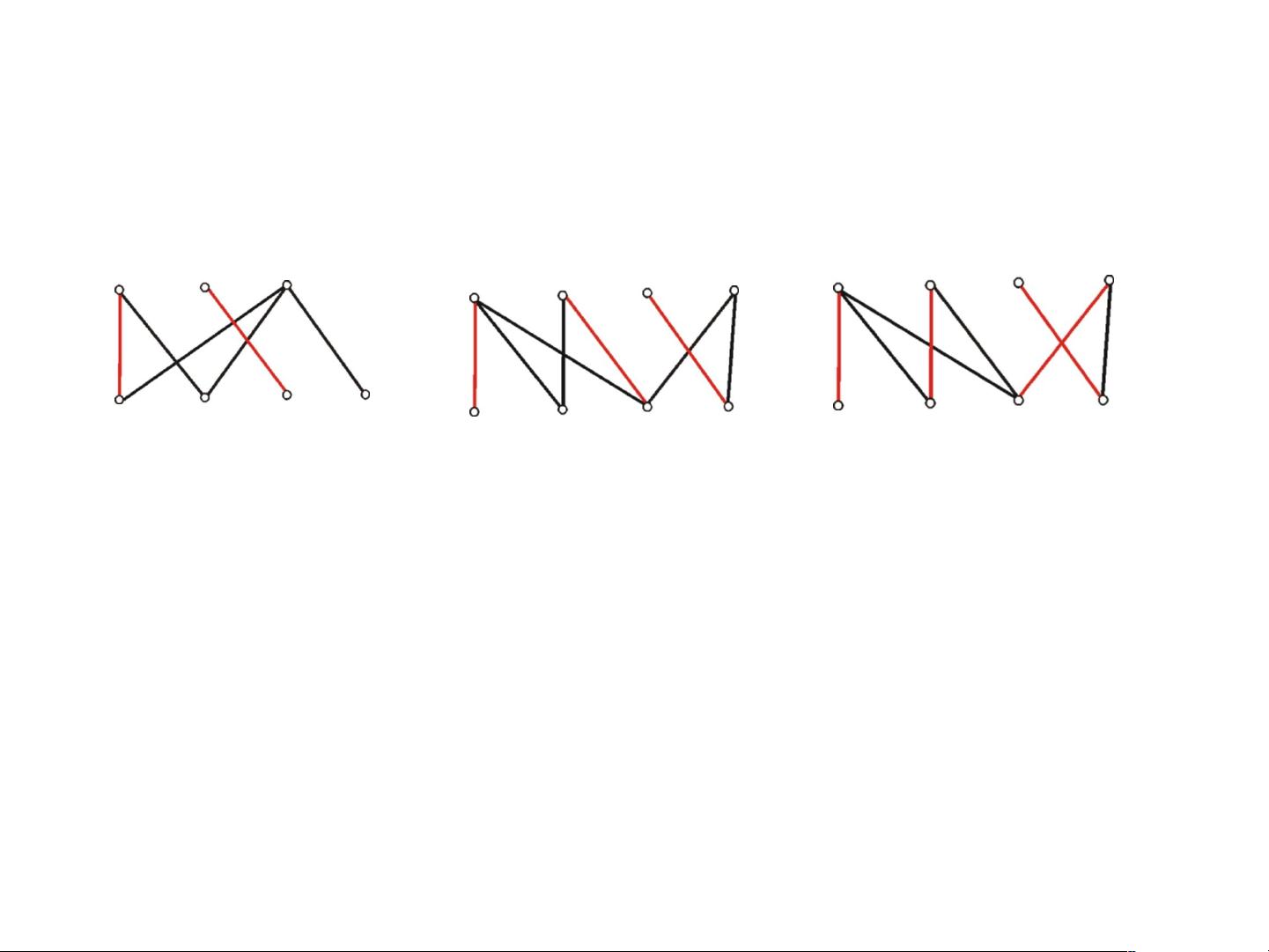
1.4 匹配 :
无向图 G=< V,E >, 取 , 若 E
’
中任意两条边均不相
邻 ,
称其为 G 的一个匹配 . 一般匹配用 M 表示 .
EE
'
1.4 极大 / 最大 / 完美匹配 :
1) 极大匹配 : 若 M 再加任一条边就不是匹配 , 则 M 是极大
匹配
2) 最大匹配 : 边数最多的极大匹配 , 最大匹配中的边数称
为
G 的匹配数 , 记为
)(G
极大匹配 极大 / 最大匹配
4)( G
3)( G
问题 : 完全二部图 K
r,s
的匹配数是多少 ?
},min{)( srG
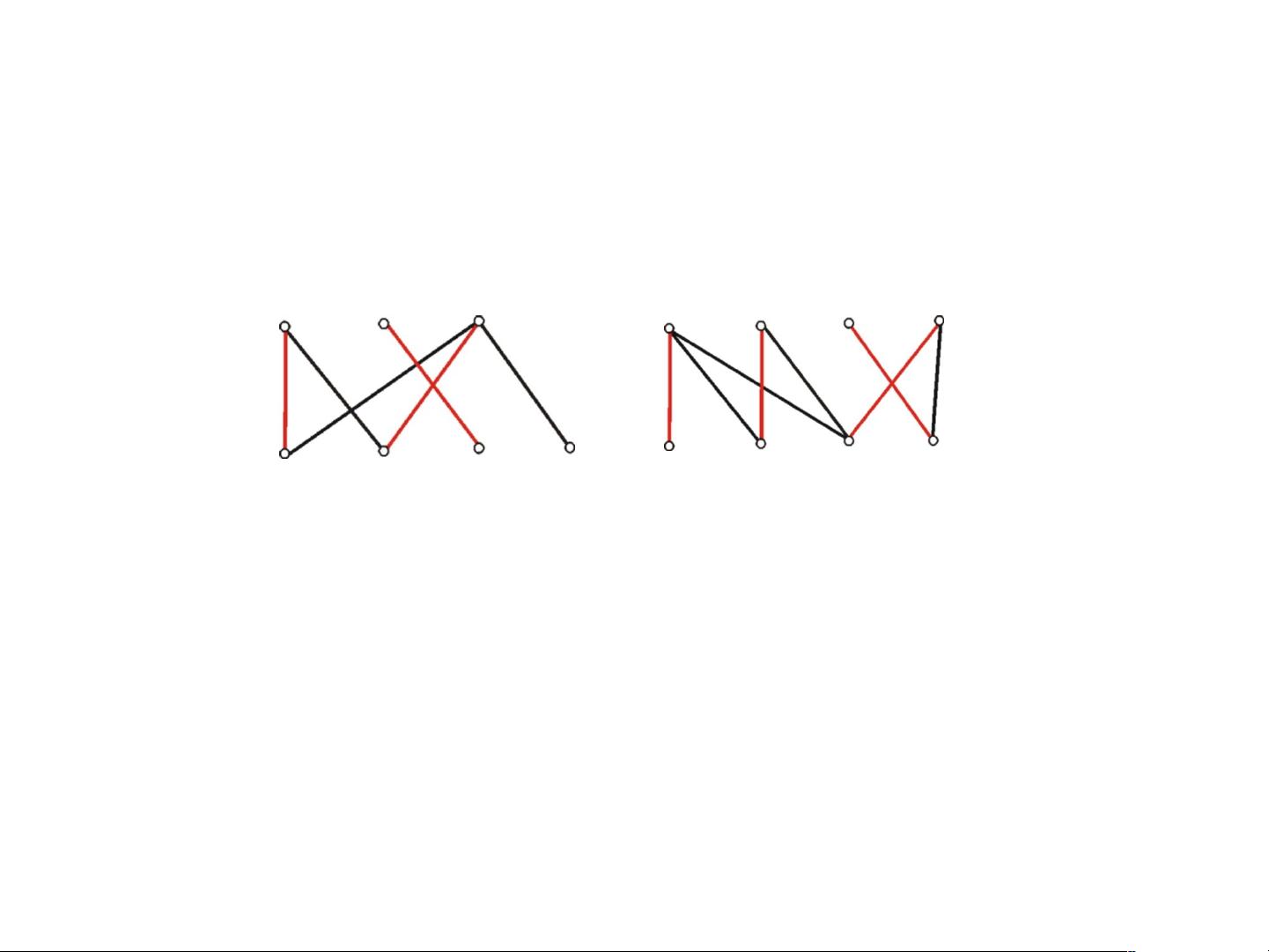
1.4 极大 / 最大 / 完美匹配 :
3)M 饱和点 :M 是 G 的匹配 , 任意 v V(G),∈ 若 v 是 M 中某
边的端
点 , 则称 v 是 M 饱和点 , 否则称 v 为 M 不饱
和点 .
4) 完美匹配 : 若任意 v V(G)∈ 均是 M 饱和点 . 称 M 为完美
匹配 .
完美匹配
M 饱和点 :a,b,c,d,e,
f
a b
c
d e
f
g
M 不饱和点 :g
全是 M 饱和
点
a b
c
d
e
f
g h
显然有完美匹配的无向图 G 必有偶数个顶点 .
















