DSA 数字签名算法源代码及流程图
DSA(Digital Signature Algorithm,数字签名算法)是一种常用的基于公钥密码学的数字签名算法。它是由 NIST(National Institute of Standards and Technology,美国国家标准技术研究所)于 1991 年发布的,用于生成和验证数字签名。
DSA 算法的主要功能
DSA 算法的主要功能是生成和验证数字签名。它需要一个安全的随机数生成器来生成密钥对,并使用 Miller-Rabin 素性测试来验证生成的素数。
DSA 算法的流程图
DSA 算法的流程图可以分为以下几个步骤:
1. 生成随机数:使用随机数生成器生成一个 16 位的大素数 q 和一个 32 位的大素数 p,其中 q 是 p-1 的因子。
2. 生成密钥对:使用 p 和 q 生成一个密钥对(公钥、私钥)。
3. 签名生成:使用私钥对消息进行签名。
4. 签名验证:使用公钥对签名进行验证。
DSA 算法的主要函数
DSA 算法中有以下几个主要函数:
1. `long long ksm(long long a, long long b, long long c)`: 计算 a^b%c 的结果。
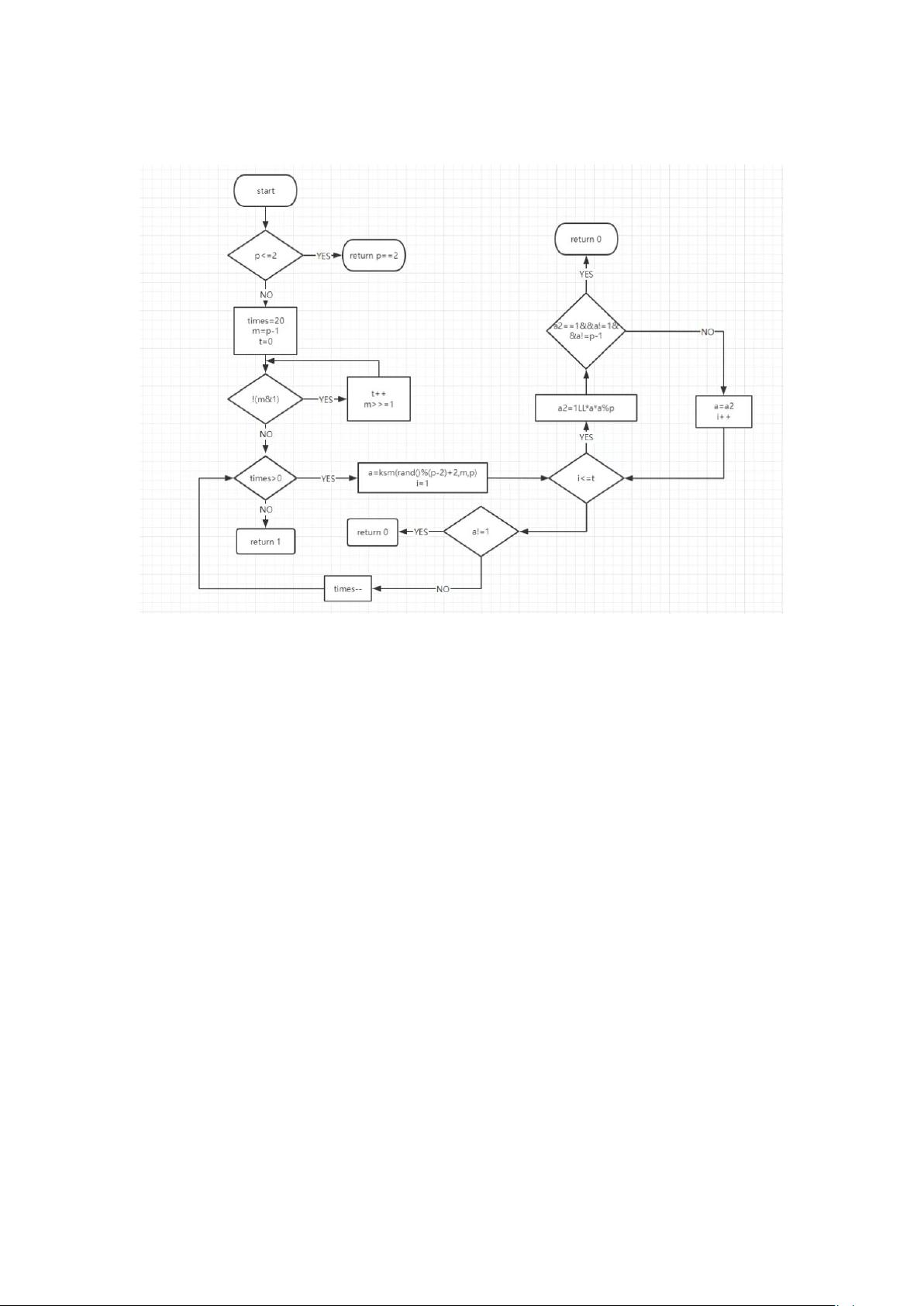
2. `long long Miller_Rabin(long long p)`: 对素数 p 进行 Miller-Rabin 素性测试。
3. `long long rndBigPrime16()`: 生成一个 16 位的大素数。
4. `long long rndBigInt32()`: 生成一个 32 位的大数。
DSA 算法的实现
以下是 DSA 算法的实现代码:
```c
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <climits>
#include <ctime>
#include <vector>
#include <assert.h>
using namespace std;
long long ksm(long long a, long long b, long long c) {
// a^b%c
long long ans = 1, base = a;
while (b) {
if (b & 1) ans = ans * base % c;
base = base * base % c;
b >>= 1;
}
return ans;
}
long long Miller_Rabin(long long p) {
if (p <= 2) return p == 2;
if (p % 2 == 0) return 0;
long long times = 30, m = p - 1, t = 0;
while (!(m & 1)) t++, m >>= 1;
while (times--) {
long long a = ksm(rand() % (p - 2) + 2, m, p), a2;
for (long long i = 1; i <= t; ++i) {
a2 = 1LL * a * a % p;
if (a2 == 1 && a != 1 && a != p - 1) return 0;
a = a2;
}
if (a != 1) return 0;
}
return 1;
}
long long rndBigPrime16() {
// 生成一个 16 位的大素数
while (1) {
long long x = (double)rand() / RAND_MAX * (1 << 16);
if (x >= (1 << 16) || x < (1 << 15)) continue;
while (!Miller_Rabin(x)) x++;
return x;
}
}
long long rndBigInt32() {
// 生成一个 32 位的大数
while (1) {
long long x = (double)rand() / RAND_MAX * (1LL << 32);
if (x >= (1LL << 32) || x < (1 << 31)) continue;
return x;
}
}
long long hp;
long long H(long long x, long long q) {
return x * hp % q;
}
int main() {
srand((unsigned)time(NULL));
// 生成满足 q|(p-1)的大素数 p,q
long long p, q, hp = rndBigPrime16();
while (1) {
// ...
}
return 0;
}
```
DSA 算法的应用
DSA 算法广泛应用于各种安全协议和系统中,如 SSL/TLS、PGP、SSH 等。它提供了安全的数字签名和验证机制,保护数据的完整性和真实性。
DSA 算法的优缺
DSA 算法的优点是:
* 高效的签名生成和验证速度
* 安全的数字签名和验证机制
* 广泛应用于各种安全协议和系统中
DSA 算法的缺点是:
* 需要安全的随机数生成器
* 需要 Miller-Rabin 素性测试来验证生成的素数
* 可能存在侧信道攻击和 collision attacks
DSA 算法是一种常用的数字签名算法,广泛应用于各种安全协议和系统中。它提供了安全的数字签名和验证机制,保护数据的完整性和真实性。但是,它也存在一些缺点,需要在实际应用中进行合理的设计和实现。