经典的连续系统仿真建模方法学

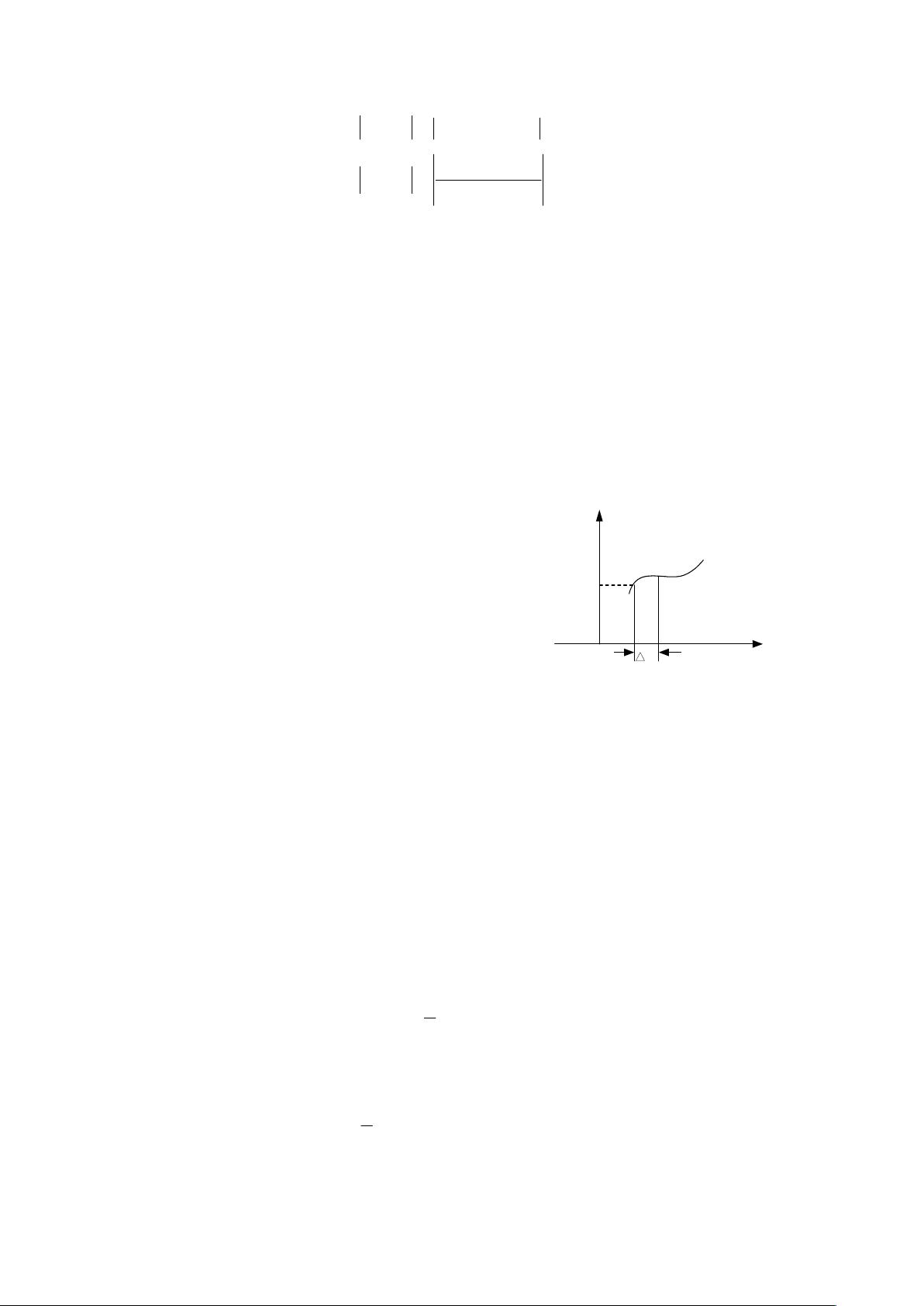
"经典的连续系统仿真建模方法学" 本资源摘要信息涵盖了经典的连续系统仿真建模方法学的基本概念、数值积分法、线性多步法等内容。 1. 连续系统仿真建模基本概念 连续系统仿真建模是指使用数字计算机对连续系统进行仿真的过程。为了实现仿真，需要将连续模型离散化，这是连续系统仿真的基础。离散化原理及要求是指数字计算机在数值及时间上的离散性与被仿真系统数值及时间上的连续性之间的基本问题。 2. 数值积分法 数值积分法是连续系统仿真中最基本的算法。对于形如y'(t) = f(t, y, u)的系统，已知系统变量y的初始条件y(t0)，现在要求y随时间变化的过程y(t)。计算过程可以考虑使用欧拉法，即用矩形面积近似表示积分结果。 3. 欧拉法 欧拉法是最经典的近似方法。当t=t1时，y(t)的近似值为y1：y(t1) = y0 + hf(t0, y0, u0)。重复上述作法，可以得到任意时刻tk+1的近似值。 4. 离散化原理 离散化原理是指数字计算机在数值及时间上的离散性与被仿真系统数值及时间上的连续性之间的基本问题。设系统模型为y'(t) = f(t, y, u)，令仿真时间间隔为h，离散化后的输入变量为û(k)，系统变量为ŷ(k)，则可认为两模型等价，这称为相似原理。 5. 相似原理 相似原理用于仿真时，对仿真建模方法有三个基本要求：（1）稳定性：若原连续系统是稳定的，则离散化后得到的仿真模型也应是稳定的。（2）准确性：有不同的准确性评价准则，最基本的准则是：原连续模型y'(t) = f(t, y, u)仿真模型ŷ(k) = f(k, ŷ(k), û(k))。（3）快速性：数字仿真是一步一步推进的，即由某一初始值y(0)出发，逐步计算，得到y(k)，每一步计算所需时间决定了仿真速度。 6. 连续系统仿真方法 连续系统仿真方法包括数值积分法、线性多步法等。数值积分法是连续系统仿真中最基本的算法，包括欧拉法、龙格-库塔法等。线性多步法是指使用线性多步法来近似连续系统的仿真模型。