
The 2011 5th Central South
Programming Contest
Contest Section
Hunan University
May 29, 2011

Problems List
A …………………… Avalon
B …………………… Be a good snooker player
C …………………… Rubik's Cube
D …………………… Digit Wave
E …………………… ElGamal Decryption
F …………………… The Least Palindromic Number
G …………………… GCD depth
H …………………… DIY Necklace
I …………………… Distinct Numbers
J …………………… Word Counting
K …………………… Blocks
The 2011 5th Central South Programming Contest
Problem A
Avalon
Description
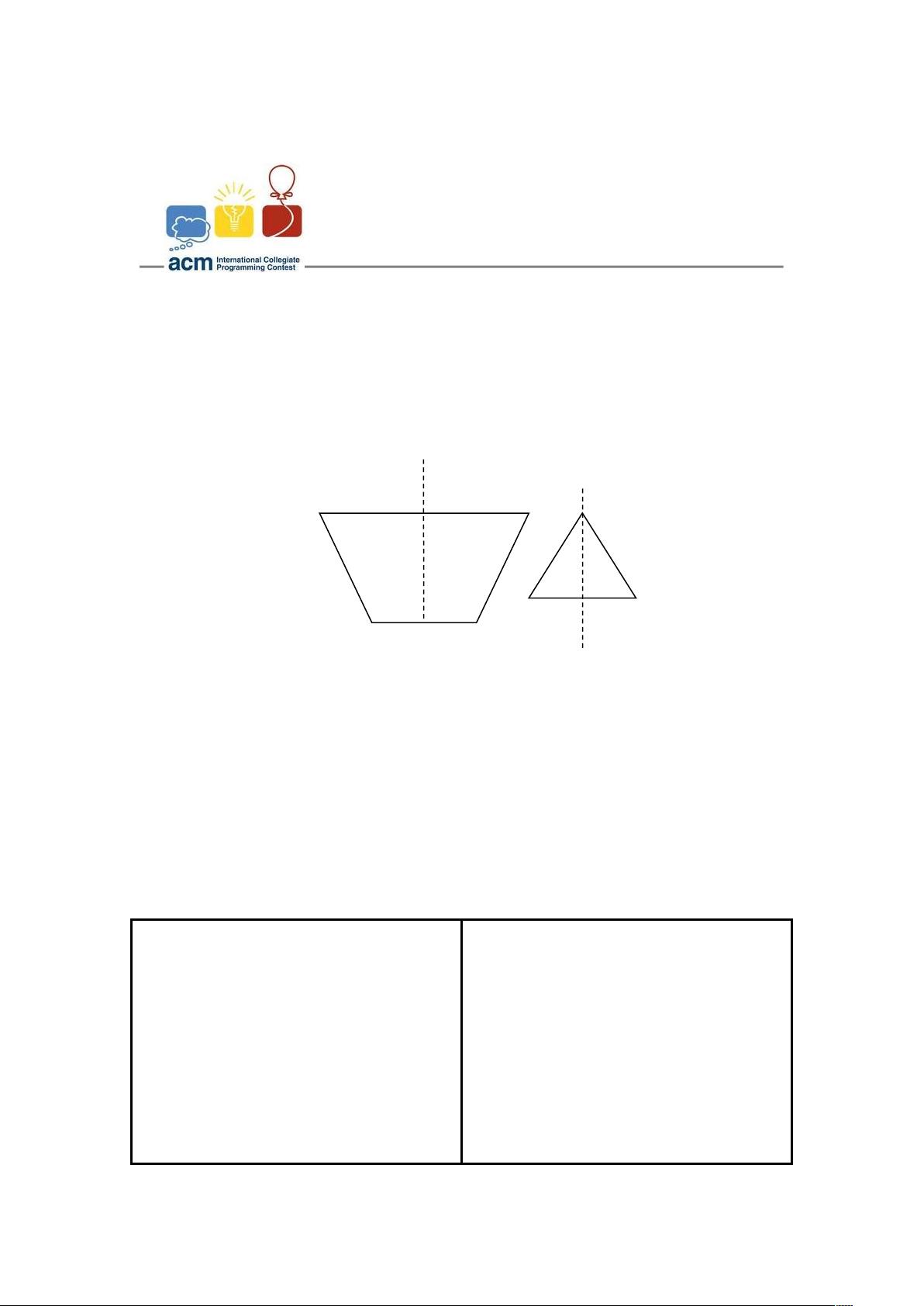
The King Arthur have a sword Excalibur. It make King Arthur win many battle.
Also He have a strong defense treasure which is his scabbard. named Avalon.
His scabbard can make a magic graph(simple polygon) named avalon, if
avalon is mirror symmetry the King Arthur can stand in it and will not be hurt
by anything.
Now the King Arthur using his scabbard, you must judge if it is Avalon.
Input
There are multiple test case in input, each test case include many rows.
#rst row is a number N means the graph have N points(3<=N<=500),next N
rows, each row have two integer x 、 y, means one of the graph’s point, the
graph is simple polygon and the points will be sorted by clockwise.
Output
. Output only one string, if the graph is Avalon puts “YES” else puts “NO”.
Sample Input Output for Sample
input
Simple test 1
3
-1 0
0 1
1 0
Simple test 2
4
-1 1
0 1
2 0
Simple test 1
YES
Simple test 2
NO

-1 0

The 2011 5th Central South Programming Contest
Problem B
Be a good snooker player
Description
Snooker is a very popular billiard game, ZZ is very interested in it, but he is not very good at
it, he always loses when playing with others, now he wants to improve his skills, he wants you to
help him solving this problem.
The game is considered playing in an 2D-plane, balls can be assumed as circles with radius R,
table is a W×H rectangle, the left-down corner of the table is (0, 0), x-coordinate increases when
you go right, and y-coordinate – up. There are also six holes which can be regarded as circles with
radius r, and their positions are: (0, 0), (W / 2, 0), (W, 0), (0, H), (W / 2, H), (W, H), for simplicity,
whenever a ball touches the hole (i.e., the intersection is not empty set, even only a point), it falls
down into it immediately. ZZ hits the cue ball (white ball) with initial velocity (V
x
, V
y
), he wants to
calculate every balls' position when all balls are stopped.
Something you should consider or pay attention to:
Gravity between the earth and the balls (the gravity accerlation g is given), no other
gravities should be considered (e.g., gravity between two balls, balls and the table, etc.);
The friction between balls and table (the friction coefficient μ is given), no other
frictions should be considered;
The initial velocity of cue ball (V
x
, V
y
);
Rebound (when hitting the table border, just assume the mass of the table is infinity),
collision (between two balls) and fall into hole;
The width of the table border should be ignored.
You can just use classical mechanics (i.e., Newton mechanics) to solve the problem, no
theory of relativity is needed.
No considering electric/magnetic fields.
In brief, just keep it simple, stupid.
Input
There are several test cases, each case contains several lines, the first line of each case is two
real numbers R (ball radius) and g (the gravity accerlation), the second line contains an integer
2<=N<=20 for the amount of balls, and real numbers W, H (width and height), r (hole radius), μ
(friction coefficient), and V
x
, V
y
(initial velocity of the cue ball).
Next N lines describe the balls, for each line, there is two real numbers x, y for the position
and an integer c for the color, (c = 0 for the cue ball, and c > 0 for other balls, and there is always
one and only one ball with c = 0).
The input will finish with the end of file, input is guaranteed that the number of test cases is


















