第k条最短路径算法

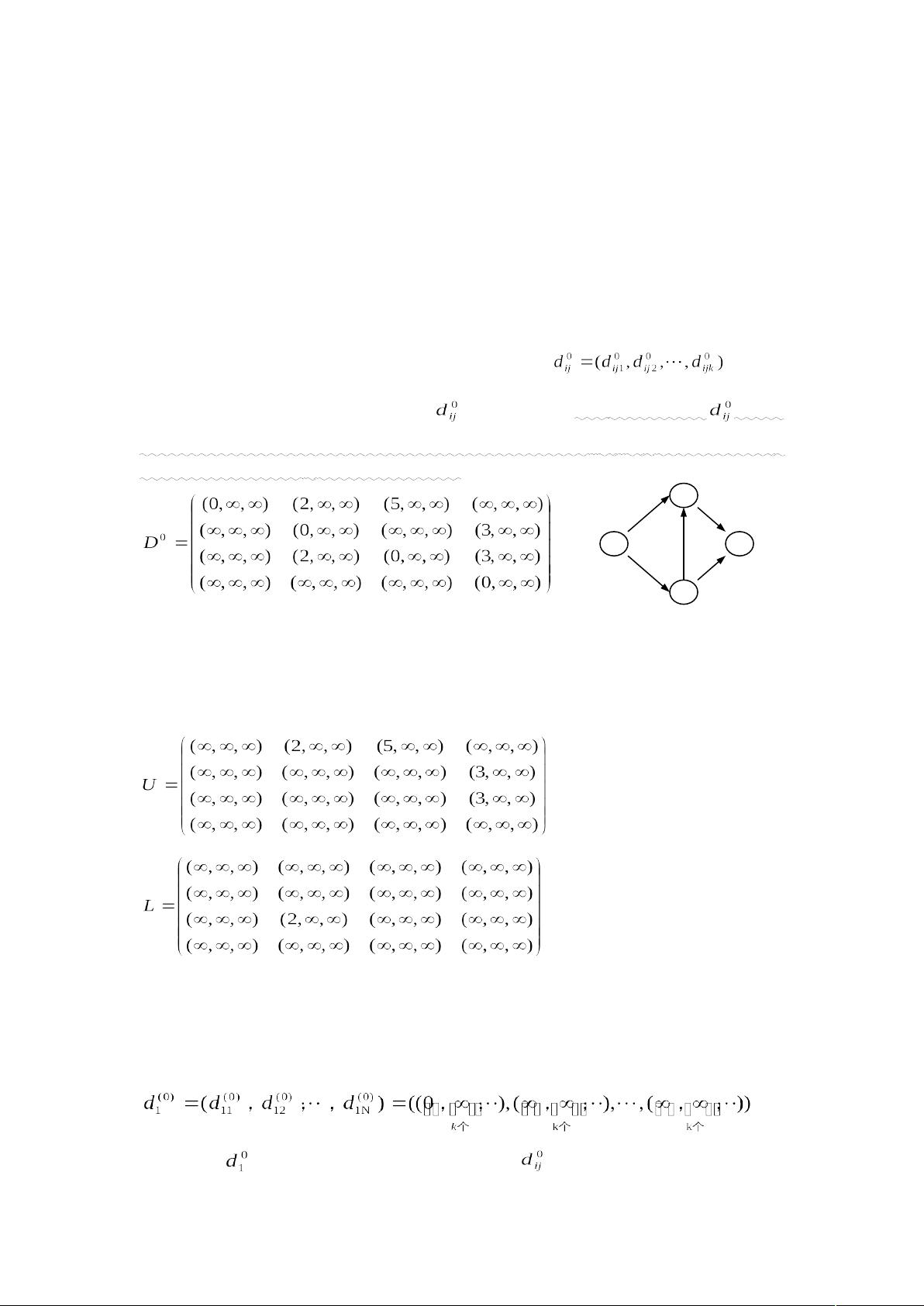
### 第k条最短路径算法知识点详解 #### 一、引言 在现代网络和通信领域，寻找两点之间的最短路径是一项基本而重要的任务。传统的单源最短路径算法（如Dijkstra算法）只能找到从起点到终点的单一最短路径。然而，在实际应用场景中，比如在网络规划、交通路线规划等领域，仅仅知道一条最短路径往往是不够的。例如，当首选路径由于某些原因无法使用时，我们需要快速切换到次优路径，甚至更次优的路径。这种情况下，**第k条最短路径算法**（简称**k最短路径算法**）就显得尤为重要。 #### 二、二重扫除算法（Double-Sweep Algorithm） 二重扫除算法是一种有效的求解第k条最短路径的方法，特别是在处理大规模网络时表现优异。 ##### 2.1 概念介绍 为了更好地理解二重扫除算法的工作原理，首先需要了解以下几个概念： - **两类运算**：推广的求极小值运算与推广的加法运算。 - **前向扫除与后向扫除**：算法的核心部分。 **两类运算**主要包括推广的求极小值运算和推广的加法运算。这些运算用于处理向量，这些向量代表了从一点到另一点的不同路径长度。 - **推广的求极小值运算**（记作 `A + B`）：对于两个向量A和B，该运算是从两个向量的所有元素中选取前k个最小的元素组成一个新的向量。 - **推广的加法运算**（记作 `A × B`）：对于两个向量A和B，该运算是将两个向量的对应元素相加后，选取前k个最小的和组成一个新的向量。 **示例**：假设A = (1, 3, 4, 8)，B = (3, 5, 7, 16)，那么： - A + B = min4{1, 3, 4, 8, 3, 5, 7, 16} = (1, 3, 4, 5) - A × B = min4{1+3, 1+5, 1+7, 1+16, 3+3, 3+5, …, 8+16} = {4, 6, 7, 8} **前向扫除与后向扫除**：这两个概念是二重扫除算法的核心组成部分。 - **前向扫除**：按照顶点号递增的顺序（即j = 1, 2, …, p），检查所有与j顶点相邻的前一个顶点i（i < j），判断从源顶点到j顶点的第k条最短路径是否可能经过这个相邻顶点i。 - **后向扫除**：与前向扫除类似，但按照顶点号递减的顺序执行（即j = p, p-1, …, 1），检查与j顶点相邻的后一个顶点i（i > j）。 ##### 2.2 算法思想介绍 二重扫除算法的基本思想是：通过前向扫除和后向扫除的过程，逐步确定从起点到每个顶点的第k条最短路径。每次迭代包括前向扫除和后向扫除两个步骤，最终收敛于正确的第k条最短路径。 ##### 2.3 算法过程 算法的具体过程可以分为以下几个步骤： 1. **初始化**：设置一个向量，用来估计从起点到各个顶点的最短路径长度。通常情况下，除了起点到自身的路径长度估计为0外，其他路径都估计为无穷大。 - 示例：如图1所示，假设k为3，那么初始化的向量`d10`可以表示为： ``` d10 = ( (0, ∞, ∞), (∞, ∞, ∞), (∞, ∞, ∞), (∞, ∞, ∞) ) ``` 2. **前向扫除与后向扫除**：根据当前的估计值，使用前向扫除和后向扫除计算新的估计值。 - 后向扫除公式：`d1(2r+1) = d1(2r+1)L + d1(2r)` - 前向扫除公式：`d1(2r+2) = d1(2r+2)U + d1(2r+1)` （其中r = 0, 1, 2, …） 3. **迭代**：重复步骤2，直到估计值不再变化或达到预设的最大迭代次数为止。 4. **结果输出**：最终的估计值即为从起点到各个顶点的第k条最短路径长度。 通过以上详细介绍，我们可以看出二重扫除算法是一种非常实用的算法，不仅能够解决第k条最短路径问题，而且在处理大型网络时具有较高的效率。这对于需要频繁计算多条备选路径的应用场景来说尤其重要。