!"#$
面积中心等效法研究
钱慧芳 毛惠丰 陈增禄
(西安工程科技学院电子信息学院
!"##$%
)
摘 要 在分析现有
&’()
面积等效方法的基础上,提出了一种
&’()
面积中心等效法。文
中给出了按照面积中心等效法合成
&’()
波形的机理以及面积中心等效算法,并对双极性面积中
心等效法生成的
&’()
波形进行了谐波分析。仿真结果表明,按面积中心等效法合成的
&’()
波
形与传统的面积等效法合成的
&’()
波形相比,其基波分量增大,低次谐波分量明显改善。
关键词
&’()
逆变器 面积中心等效 谐波分析
%
引言
采样控制理论指出:冲量相等而形状不同的窄
脉冲加在具有惯性的环节上时,其效果基本相同,
冲量即指窄脉冲面积
[
"
]
。
&’()
面积等效法的基本
原理是在各采样周期内,均用一个与正弦曲线和时
间轴所围面积相等的等高矩形脉冲来等效替代。等
面积法的谐波较规则采样法小
[
*
,
+
]
。在各采样周期
内,等效矩形脉冲均有一个在水平方向上移动的自
由度。为提高矩形脉冲序列与正弦曲线等效的程
度,必须对各采样周期内的矩形脉冲在水平方向上
的位置进行寻优。传统的面积等效法
[
*
,
+
]
是以采样
周期的几何平均中心作为等效矩形脉冲的中点;本
文提出的面积中心等效法是以每一等份的正弦波与
时间轴所围面积中心点作为等效矩形脉冲的中点。
& !"#$
面积中心等效法
& ’ %
单极性面积中心等效法
如图
"
所示,将正弦半波分为
!
等份,每一
等份的正弦曲线与
!
(令
!
,
"
"
)轴所包围的面积
都用一个与此面积相等的等高矩形脉冲来代替,即
面积等效。第
#
等份的正弦曲线与
!
轴所围平面的
面积中心的横坐标为
!
#
,将
!
#
作为第
#
等份的正
弦曲线对应的矩形脉冲与
!
轴所围平面的中心的横
坐标,即面积中心等效。这样,用
!
个等幅而不
等宽的一系列矩形脉冲所构成的波形来等效正弦半
波。正弦波的负半周也可用同样的方法来获得等效
的矩形脉冲序列。
设正弦波为
$
-
, %
.
/01
(
"
"
)
, %
.
/01
(
!
),其中,
%
.
为正弦波峰值。将正弦波的正半周分为
!
等份
(其负半周也分为
!
等份),则每一等份的宽度为
!
2 !
弧度。
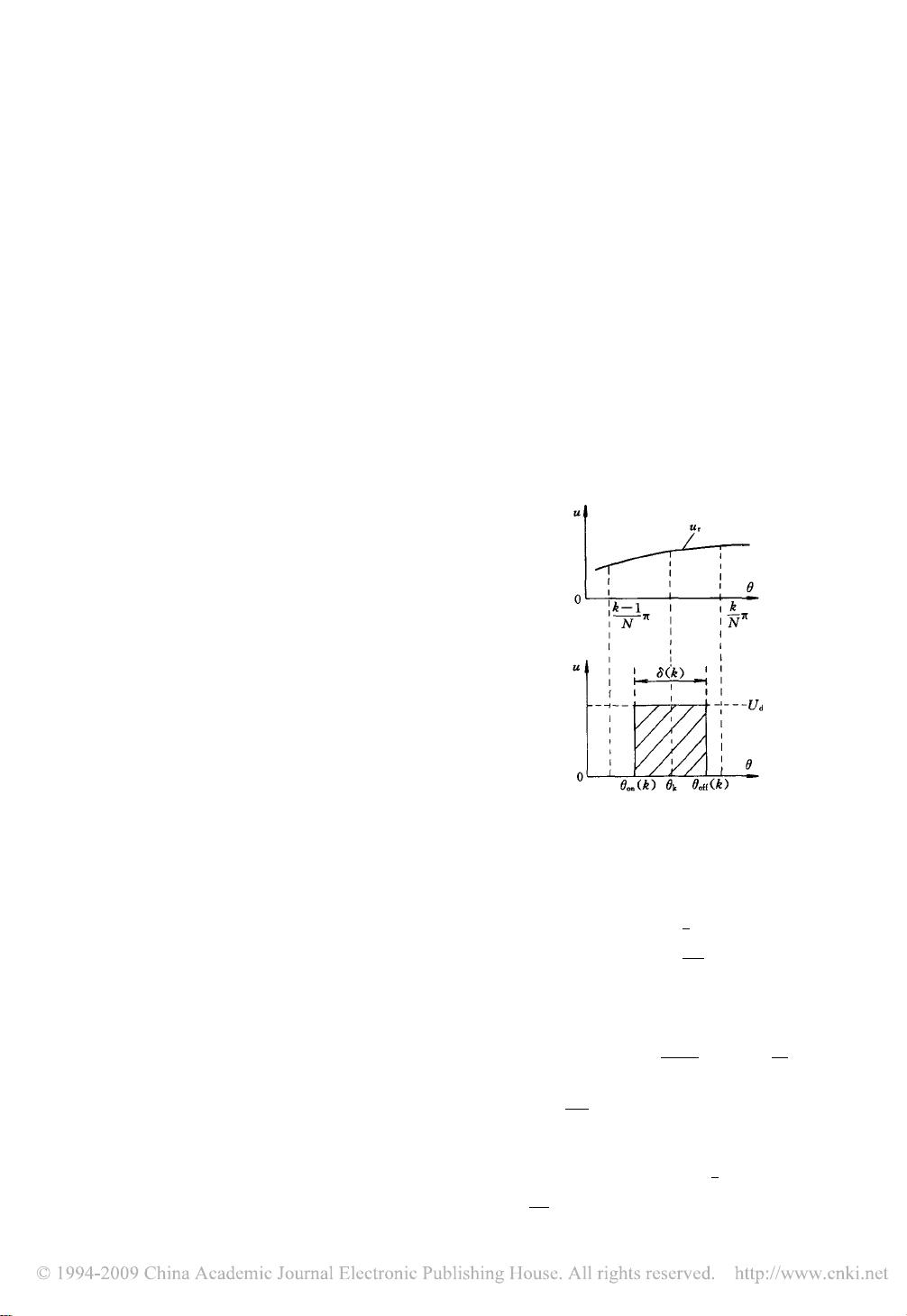
图
"
单极性
&’()
面积中心等效算法
%
3
、
#
(
#
)—等效矩形脉冲的高度、宽度
!
41
(
#
)、
!
455
(
#
)—等效矩形脉冲的开通角、关断角
根据面积等效原理,可得
#
(
#
)
%
3
&
%
.
!
#
!
!
#
’
"
!
!
/01
(
!
)
3
(
!
)
(
# , "
,
*
,
+
,…,
!
) (
"
)
由式(
"
)得
#
(
#
)
, ( 64/
(
# 7 "
!
!
)
7 64/
(
#
!
!
[ ]
) (
*
)
式中,
( ,
%
.
%
3
。
根据面积中心等效原理,可得
!
!
#
#
’
"
!
!
%
.
/01
(
!
)
3
(
!
)
&
!
#
!
!
!
#
%
.
/01
(
!
)
3
(
!
)(
+
)
由式(
+
)得
—
)*+
"""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""""
—
·
电力电子
·
《电气应用》
!""#
年第
!$
卷第
%
期















