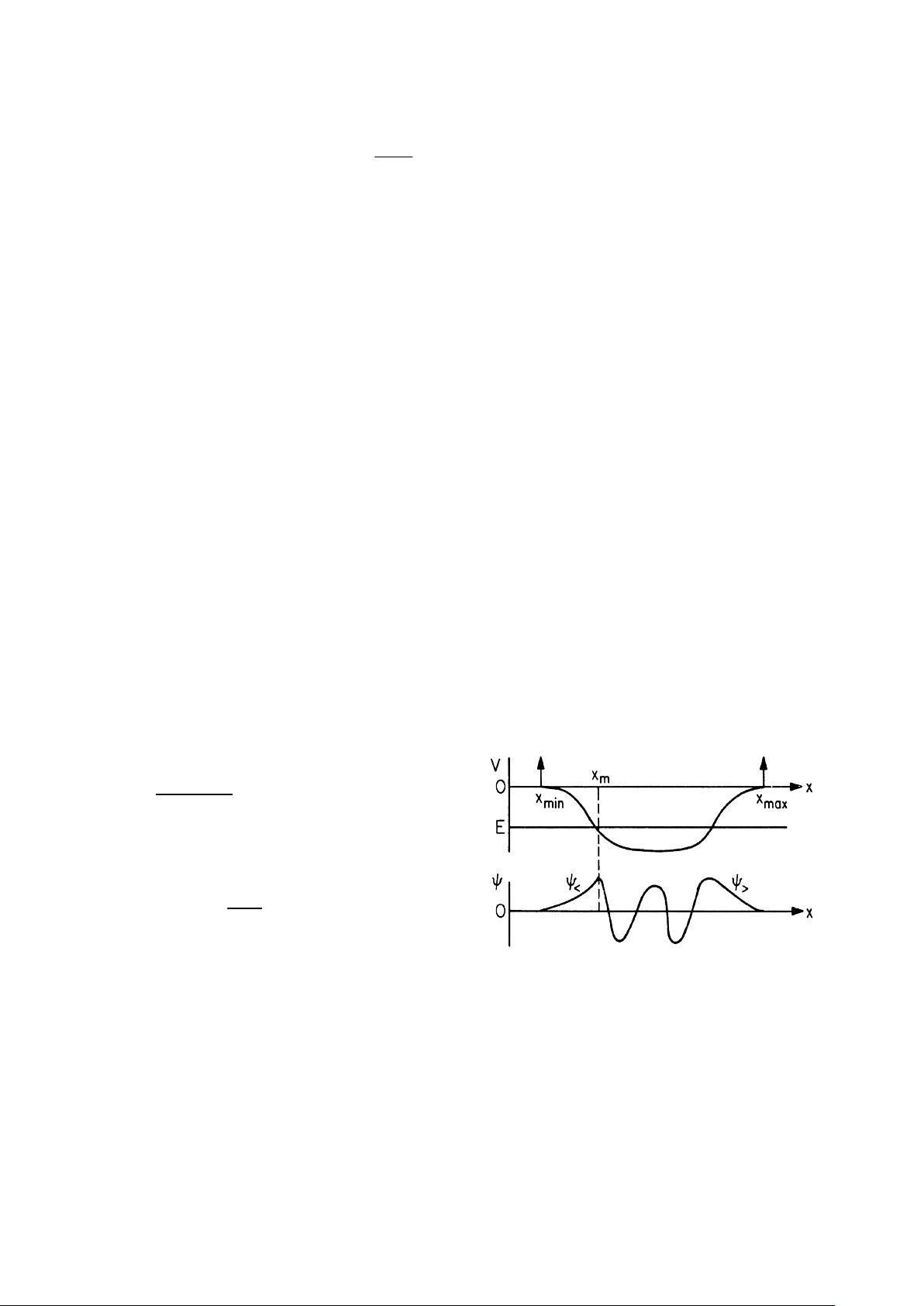
一维薛定谔方程的定态解

### 一维薛定谔方程的定态解 #### 问题背景与描述 在一维空间内，薛定谔方程描述了量子力学系统中粒子的状态随时间的变化规律。当考虑系统的定态行为时，即粒子处于特定能量状态时的行为，我们可以使用定态薛定谔方程来求解。定态薛定谔方程的形式如下： \[ -\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2} + V(x)\psi(x) = E\psi(x) \] 其中，\(\hbar\) 是约化普朗克常数，\(m\) 是粒子的质量，\(V(x)\) 表示势能函数，\(E\) 表示系统的总能量，\(\psi(x)\) 是波函数。 本问题旨在通过数值方法求解上述方程，并寻找使该方程有非零解的能量本征值 \(E\) 及其相应的波函数 \(\psi(x)\)。为此，文中提到了两种常用的方法：打靶法（shooting method）和 Numerov 方法。 #### 常见势阱分析 文中给出了两种常见的一维势阱模型作为例子： 1. **无限深平底势阱**：势能函数 \(V(x)\) 在区间 \([-1, 1]\) 内为 0，在区间之外趋于无穷大。数学形式如下： \[ V(x) = \begin{cases} 0 & -1 < x < 1 \\ \infty & \text{otherwise} \end{cases} \] 2. **一维谐振子**：势能函数 \(V(x)\) 为 \(V(x) = \frac{1}{2}m\omega^2x^2\)，其中 \(\omega\) 是振动频率。数学形式如下： \[ V(x) = \begin{cases} \frac{1}{2}m\omega^2x^2 & -1 < x < 1 \\ \infty & \text{otherwise} \end{cases} \] #### 打靶法求解本征值问题 打靶法是一种解决二阶常微分方程边值问题的有效方法，适用于求解薛定谔方程中的本征值问题。其基本思路是： - **选择一个初始本征值估计**：假设一个本征值 \(E\) 的初始估计值。 - **构造初值问题**：将原定态薛定谔方程转化为一个初值问题，即给定初值条件。 - **积分**：从某一端点出发（如 \(x_{\text{min}}\)），对微分方程进行数值积分，得到一个数值解。 - **比较结果**：在另一端点（如 \(x_{\text{max}}\) 或接合点 \(x_m\)）比较数值解与边界条件。 - **调整本征值估计**：根据比较结果调整 \(E\) 的值，直至满足边界条件。 具体来说，在每一步中，我们需要： 1. **数值积分**：使用数值积分方法（如龙格-库塔方法、Numerov 方法等）求解微分方程。 2. **接合点选择**：选择合适的接合点 \(x_m\)，使得两端的积分都是准确的。 3. **调整本征值**：根据两端数值解的匹配情况调整本征值的估计，直至满足边界条件。 #### Numerov 方法 除了打靶法外，Numerov 方法也是一种高效的数值积分方法，特别适用于求解薛定谔方程。该方法基于泰勒展开和微分方程的近似，可以有效减少积分过程中的误差累积。Numerov 方法的核心在于构造一个迭代公式，用于逐步计算波函数在不同点上的值。 ### 实现细节 #### 无量纲化 在实际计算过程中，通常会进行无量纲化处理，即将原方程转换为无量纲形式，以简化计算并提高数值稳定性。例如，通过引入新的变量和参数，原方程可以被改写为： \[ -\frac{d^2\phi(x)}{dx^2} + v(x)\phi(x) = \epsilon\phi(x) \] 这里，\(\epsilon\) 是无量纲化的能量本征值，\(v(x)\) 是无量纲化的势能函数。 #### 算法步骤 1. **初始化**：选取一个初始估计值 \(\epsilon_0\) 和一个初始点 \(x_{\text{min}}\)。 2. **数值积分**：从 \(x_{\text{min}}\) 开始向前积分至接合点 \(x_m\)，得到数值解 \(\psi_<\)；从 \(x_{\text{max}}\) 开始向后积分至 \(x_m\)，得到数值解 \(\psi_>\)。 3. **归一化**：调整 \(\psi_<\) 和 \(\psi_>\)，使二者在接合点 \(x_m\) 处相等。 4. **比较微商**：比较 \(\psi_<\) 和 \(\psi_>\) 在 \(x_m\) 处的微商是否相等。若不相等，则调整 \(\epsilon\) 并重复步骤 2 和 3。 5. **终止条件**：若 \(\psi_<\) 和 \(\psi_>\) 在 \(x_m\) 处的微商相等，则认为找到了一个能量本征值。 #### 总结 本文主要介绍了如何通过打靶法和 Numerov 方法求解一维定态薛定谔方程中的本征值问题。这两种方法都是数值计算中的重要工具，可以帮助我们有效地求解复杂的量子力学问题。通过对无限深平底势阱和一维谐振子两种典型势阱的分析，我们可以进一步理解这些方法的应用场景和技术细节。通过上述步骤，我们能够获得能量本征值以及对应的波函数，从而揭示出量子系统在特定势场下的行为特征。