基于Matlab的RC一阶电路仿真

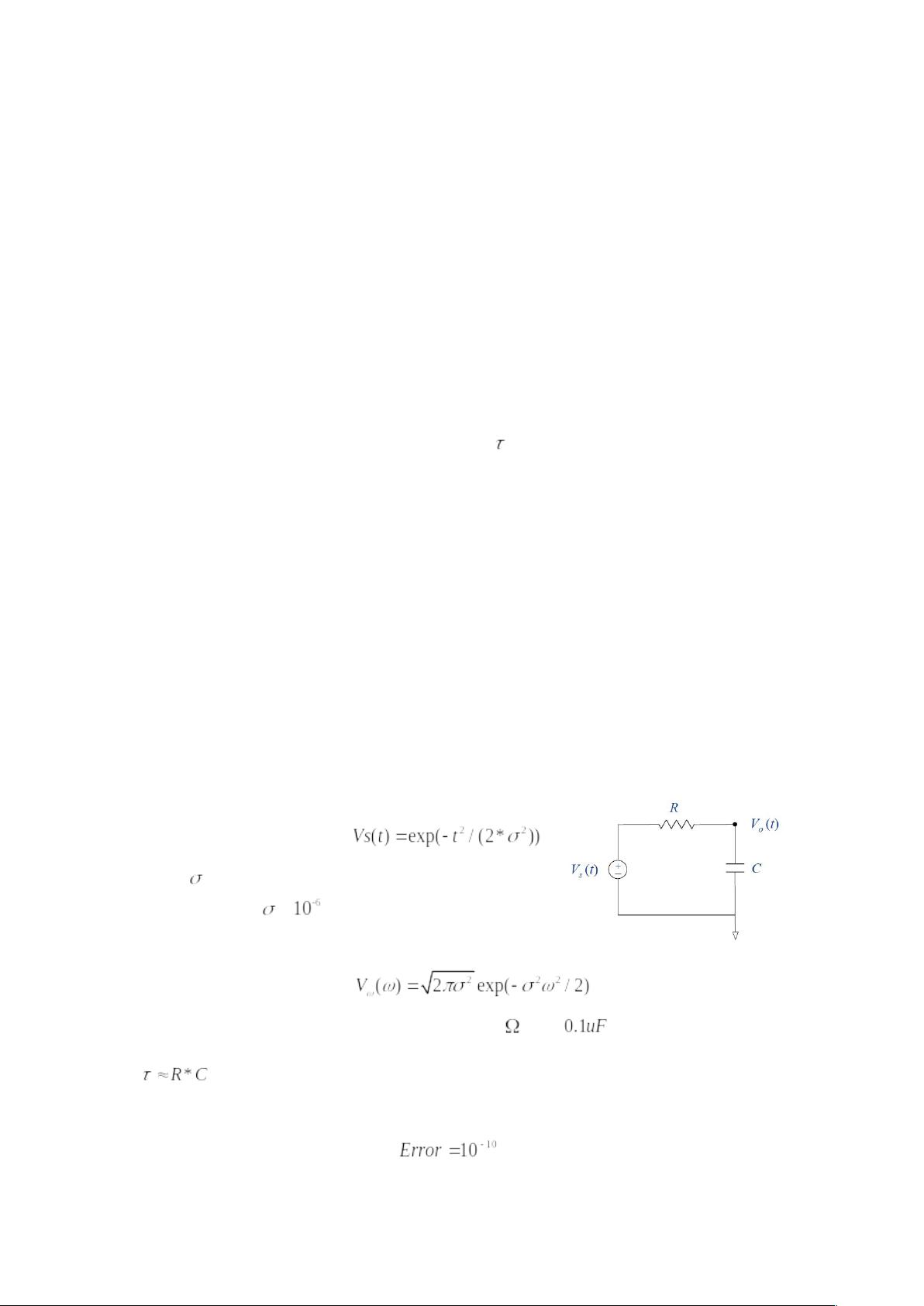
RC一阶电路是电子工程领域中的基础概念，它由一个电容C和一个电阻R串联组成，常用于滤波、积分、微分等应用。在本主题中，我们将深入探讨如何利用Matlab进行一阶RC电路的仿真，包括时域分析和频域分析。 让我们了解RC一阶电路的基本原理。当电路接通电源后，电容C通过电阻R进行充电，电压会随着时间以指数方式增长，直到达到电源电压。这个过程可以用微分方程来描述，即 RC * dV/dt = V - V_s，其中V_s是电源电压，V是电容上的电压。解这个微分方程，我们可以得到电压随时间的变化关系。 在Matlab中，我们可以使用Simulink或者内置的电路仿真工具（如SimElectronics）来进行一阶RC电路的仿真。Simulink是一个图形化的建模仿真环境，用户可以通过拖拽模块构建电路模型。对于RC电路，我们需要添加电压源、电阻和电容模块，并连接它们。然后设置初始条件和仿真时间范围，运行仿真即可得到时域响应。 时域分析通常关注的是电路的瞬态响应，即电路在电源接通或断开后的电压或电流变化。Matlab可以绘制出电压或电流随时间的变化曲线，帮助我们理解电路的行为。在分析过程中，关键参数是时间常数τ=RC，它决定了电路从一个状态过渡到另一个状态所需的时间。 另一方面，频域分析关注的是电路对不同频率信号的响应。在Matlab中，我们可以使用傅里叶变换来分析电路的频率特性。通过设置不同的正弦波输入频率，观察输出电压的变化，我们可以得到电路的频率响应函数。这有助于我们了解电路作为滤波器的性能，比如低通、高通或带通滤波特性。 在提供的压缩包中，除了Matlab仿真代码外，还有一份课程报告，这可能是对整个仿真实验的详细记录和解释，包括实验目的、理论背景、仿真步骤、结果分析和结论。通过阅读这份报告，初学者可以更全面地理解和掌握RC一阶电路的工作原理以及Matlab仿真的方法。 学习基于Matlab的RC一阶电路仿真，不仅可以帮助我们理解基本的电路理论，还能提升我们的计算和建模技能。通过实践，我们可以掌握如何利用Matlab工具进行电路设计和分析，这对于未来在电子工程或相关领域的学习和工作都是非常有益的。