Find median of two sorted arrays
Share my O(log(min(m,n)) solution with explanation
To solve this problem, we need to understand "What is the use of median". In statistics, the median is used for dividing a
set into two equal length subsets, that one subset is always greater than the other. If we understand the use of
median for dividing, we are very close to the answer.
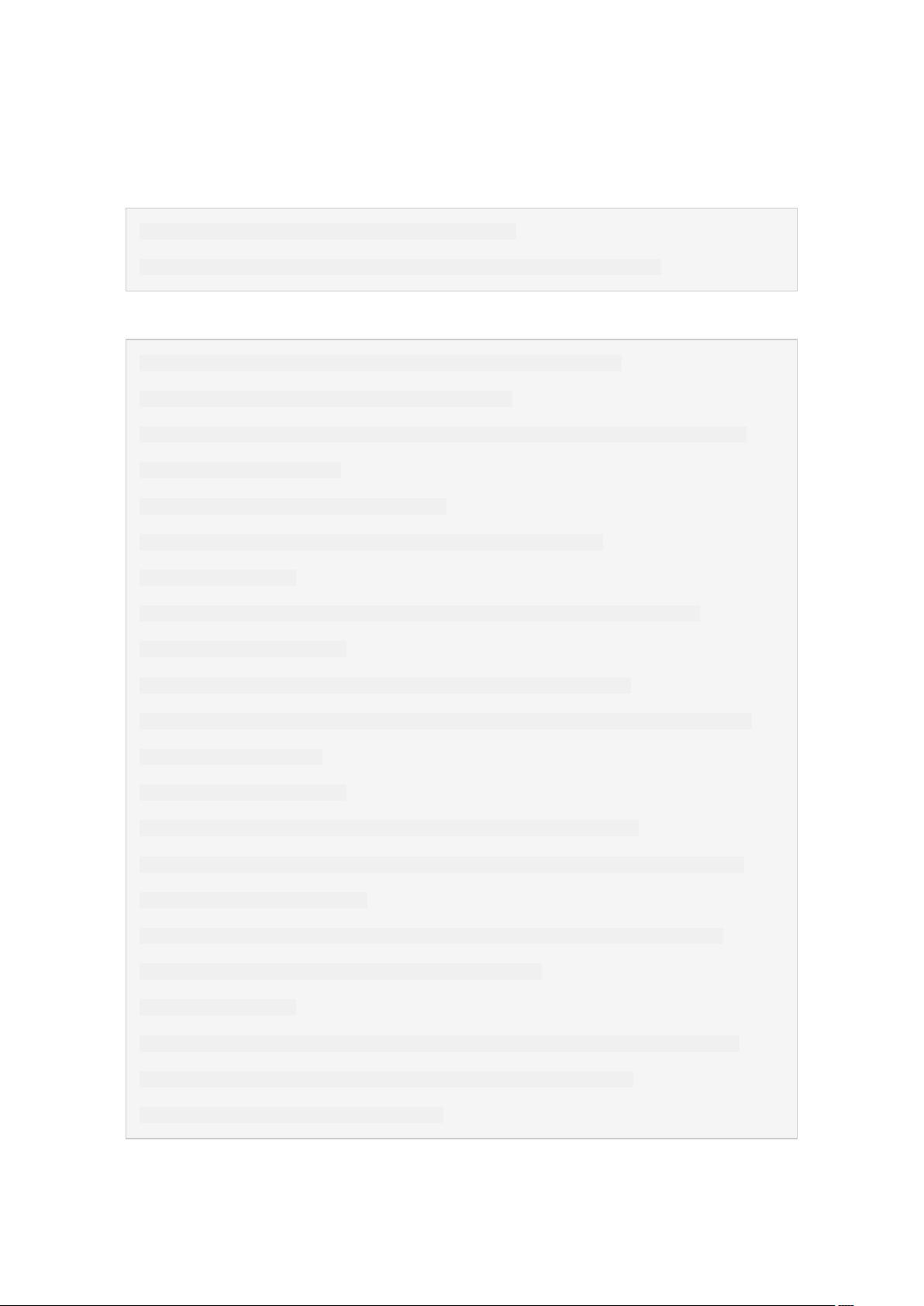
First let's cut A into two parts at a random position i:
left_A | right_A
A[0], A[1], ..., A[i-1] | A[i], A[i+1], ..., A[m-1]
Since A has m elements, so there are m+1 kinds of cutting( i = 0 ~ m ). And we know: len(left_A) = i, len(right_A) = m - i .
Note: when i = 0 , left_A is empty, and when i = m , right_A is empty.
With the same way, cut B into two parts at a random position j:
left_B | right_B
B[0], B[1], ..., B[j-1] | B[j], B[j+1], ..., B[n-1]
Put left_A and left_B into one set, and put right_A and right_B into another set. Let's name
them left_part and right_part :
left_part | right_part
A[0], A[1], ..., A[i-1] | A[i], A[i+1], ..., A[m-1]
B[0], B[1], ..., B[j-1] | B[j], B[j+1], ..., B[n-1]
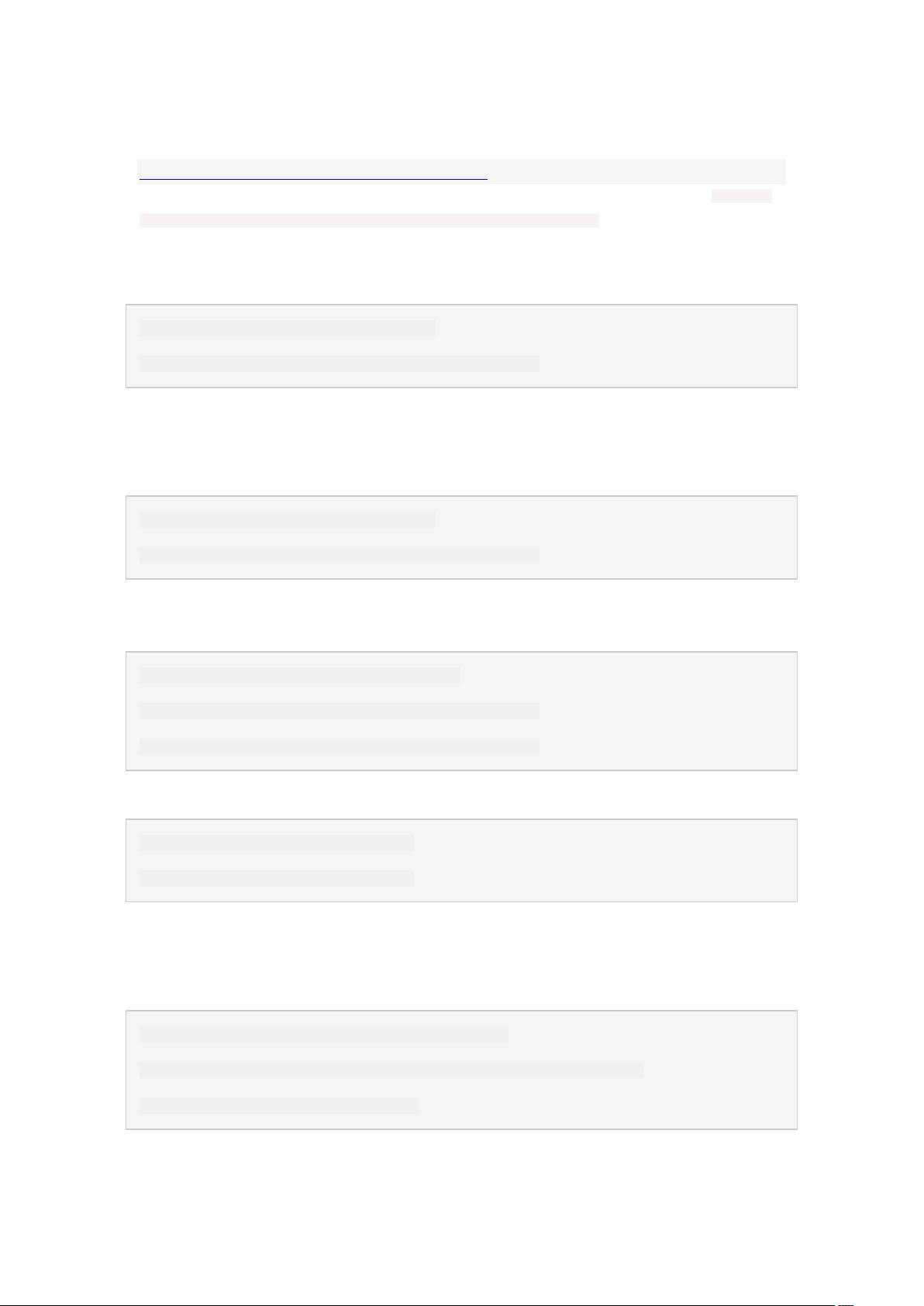
If we can ensure:
1) len(left_part) == len(right_part)
2) max(left_part) <= min(right_part)
then we divide all elements in {A, B} into two parts with equal length, and one part is always greater than the other.
Then median = (max(left_part) + min(right_part))/2.
To ensure these two conditions, we just need to ensure:
(1) i + j == m - i + n - j (or: m - i + n - j + 1)
if n >= m, we just need to set: i = 0 ~ m, j = (m + n + 1)/2 - i
(2) B[j-1] <= A[i] and A[i-1] <= B[j]
ps.1 For simplicity, I presume A[i-1],B[j-1],A[i],B[j] are always valid even if i=0/i=m/j=0/j=n . I will talk about how to deal
with these edge values at last.